4.4 Кінетичне рівняння Больцмана для електрона в кристалі. Електропровідність металів

У стані рівноваги всі вільні електрони беруть участь у невпорядкованому тепловому русі. При цьому, виходячи із симетрії функції розподілу, кількість електронів, що рухаються у протилежних напрямках, однакова, а, отже, макроскопічні електричні струми відсутні. Якщо до зразка прикладено електричне поле, то, рухаючись під його дією, електрон набуде не тільки додаткової швидкості , а й додаткової енергії . Якби ніякі процеси не перешкоджали збільшенню швидкості електрона, то вона нескінченно б зростала. Але в дійсності електрони час від часу зіштовхуються один з одним, з фононами та дефектами. У зв’язку з цими процесами було введено величину - середній час релаксації, час впродовж якого електрон безперешкодно прискорюється. Отже, для того щоб підтримувався стаціонарний стан, необхідне існування таких зіткнень, при яких електрон міг би втрачати не тільки імпульс, а й додаткову енергію. Зіткнення першого типу (тобто без значних втрат енергії) називаються пружними, другого – непружними. Розгляд цих процесів [16] показав, що можливі два типи майже пружних зіткнень електронів – з дефектами і акустичними фононами і два непружних – з оптичними фононами та міжелектронні, які відіграють суттєву роль лише в обмеженому інтервалі температур і концентрацій. Отже, рівнянь напівкласичної динаміки, наприклад (3.15), виявилося недостатнім для розрахунку інтегральних характеристик твердого тіла, які визначаються блохівськими електронами, - провідності, потоку тепла та ін. Необхідно знати ще нерівноважну функцію розподілу , оскільки проходження струму - це нерівноважний процес. На відміну від п. 4.2, де використосувалася функція розподілу за енергіями, функція - функція розподілу у -просторі (-просторі), яка визначається так: середнє число електронів, що знаходяться у деякому нерівноважному стані з квазіімпульсом в n-й енергетичній зоні в елементі об’єму в момент часу t , становить . Якщо n-а енергетична зона заповнена повністю, то густина струму в ній (і потік енергії, яку переносять електрони) дорівнює нулю [12]. Якщо n-а енергетична зона заповнена не повністю (наприклад, у металах), то густина струму в ній

, (4.6)

де - частка функції розподілу Фермі-Дірака, яка пов'язана лише із тими електронами, які беруть участь в електропровідності (їх енергетичні стани розміщуються у розмитті функції Фермі-Дірака, яка показана на рис. 4.3).

Для знаходження функції використовується кінетичне рівняння Больцмана

, (4.7)

де - градієнт функції розподілу в напрямку ; - градієнт функції розподілу в напрямку .

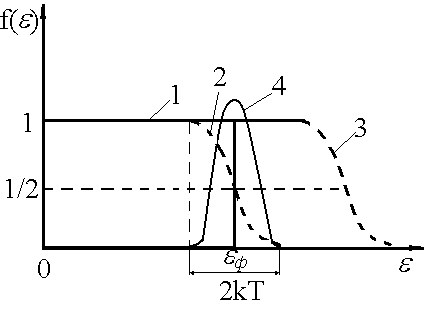
Рисунок 4.3 - Розмиття функції Фермі-Дірака при збільшенні енергії електрона: 1 - при Т=0К; 2 - при Т>0К і ; 3- при Т>0К і ; 4 - для кривої 2

У лівій частині рівняння (4.7), яке розглянуто в [17, 18], стоятиме нуль за відсутності зіткнень електронів з іншими частинками чи квазічастинками у відповідності до теореми Ліувілля. Теорема стверджує: об’єм елемента фазового простору зберігається під час руху, якщо відсутні зіткнення (тобто зберігається і число частинок), отже, функція розподілу залишається постійною, а .

У реальному кристалі відбуваються процеси зіткнення електронів із фононами, дефектами, домішками та електронами і тому в правій частині замість нуля необхідно записати похідну змінної функції розподілу - , яку Больцман назвав інтегралом зіткнень, оскільки при її обчисленні необхідно інтегрувати за всіма змінними, що впливають на імовірність зіткнень. Тоді кінетичне рівняння у самому загальному випадку запишеться так:

, (4.8)

де - сила, яка діє на електрон; - середня швидкість дрейфу електрона у зовнішньому електричному полі.

Труднощі при розв’язанні (4.8) вимагають використання наближення часу релаксації, що дає можливість записати інтеграл зіткнень у вигляді

, (4.9)

де f₀ – локально і миттєво рівноважна функція розподілу (вона була б, якщо при даних мала б місце рівновага); - параметр, що визначає швидкість наближення до рівноваги (час релаксації), .

Припущення (4.8) означає, що швидкість зміни числа частинок у даному стані пропорційна відмінності цього числа від того, яке б було за умови, що миттєві значення всіх параметрів, що впливають на нього, були б «заморожені», і мала б місце рівновага.

Для розрахунку електричної провідності металів скористаємося співвідношенням (4.6). Нерівноважну функцію можна знайти із кінетичного рівняння Больцмана (4.8). Для спрощення, розглянемо випадок однорідного стаціонарного струму за відсутності магнітного поля і градієнта температур та, скориставшись наближенням (4.9). При цьому функція f буде залежати лише від () і матиме вигляд

.

Позначимо і вважатимемо електричне поле малим та, враховуючи рівняння напівкласичної динаміки (3.15), отримаємо для статичної електропровідності

. (4.10)

Підставивши (4.10) у співвідношення (4.6), отримаємо

, (4.11)

де - похідна функції розподілу до прикладення зовнішнього електричного поля (рис. 4.3);

- час, який необхідний для переходу розподілу 3 на рис. 4.3 у розподіл 2 (час релаксації).

Для аналізу температурної залежності питомого опору металевого провідника достатньо виділити із (4.11) множник, який пов'язаний із питомою провідністю, скориставшись законом Ома в диференціальній формі . Отже, питома провідність у випадку ізотропного середовища - скаляр (напрямки збігаються):

. (4.12)

Оскільки основний внесок в електропровідність металів дають електрони із розмиття функції Фермі-Дірака, то попередній вираз спрощується до вигляду

,

де - густина енергетичних станів на рівні Фермі (рис. 4.4); v_ф – середня швидкість електронів на поверхні Фермі.

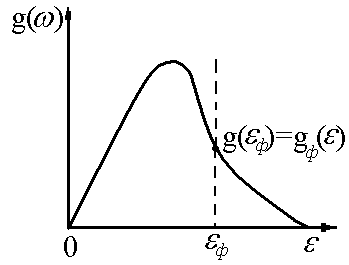
Рисунок 4.4 - Залежність густини енергетичних станів електронів від енергії

Після відповідних перетворень (в граничному випадку вільних електронів) можна одержати співвідношення, яке випливає з класичної теорії Друде і з квантової теорії Зоммерфельда:

. (4.13)

Величина визначається механізмами розсіяння електронів. Якщо таких механізмів є декілька, то їх вклади в , тобто (відповідно до формул (4.12) та (4.13)) в питомий опір є адитивними. Це твердження називають правилом Матіссена. Як зазначалося вище, електрони в твердому тілі розсіюються на всіх порушеннях періодичності кристалічної структури (на статичних і динамічних). Внесок статичних дефектів у питомий опір суттєво не залежить від температури, і вони визначають залишковий (при Т0К) питомий опір . Найважливішими із динамічних порушень періодичності є фонони. Розрахунки і експеримент показують, що механізм розсіяння електронів на фононах дає основний внесок в [12]. На рис. 4.5 наведена температурна залежність питомого опору металу, обумовлена розсіянням електронів на фононах . У двох граничних випадках: при високих температурах (Т>>) ~~T; при низьких температурах (Т<<) ~~. При проміжних значеннях температури (0<Т<) ~Тⁿ, де 1<n<5.

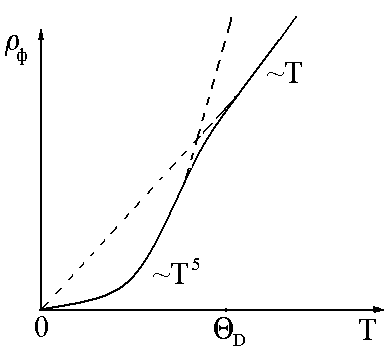
Рисунок 4.5 - Температурна залежність опору металу, обумовлена роз-сіянням електронів на фононах

Додатково внесок в питомий опір металів можуть додавати і розсіяння електронів на магнонах (ефект Кондо), і розсіяння електронів на електронах, вплив якого на опір пояснюється з позицій Фермі-рідини Ландау [19].