Питання і завдання до розділу 3

1. Запишіть рівняння Шредінгера для кристала і поясніть величини, що до нього входять.

2. Поясніть суть наближень, які описують стан зовнішніх електронів у кристалах.

3. Поясніть суть методів сильного зв’язку та майже вільних електронів.

4. Запишіть і поясніть умову періодичності потенціального поля кристала.

5. Запишіть функцію Блоха і сформулюйте відповідну теорему.

6. Назвіть особливості 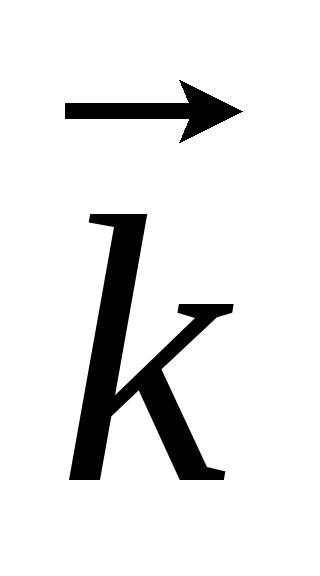, який характеризує стан хвильової функції електрона в кристалі.

7. Поясніть, чому частинки, що рухаються в кристалах і описуються векторами 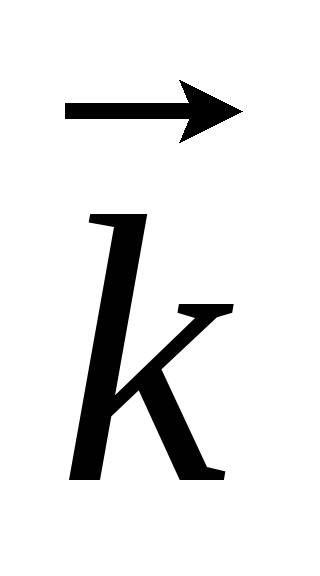, називають квазічастинками.

8. Поясніть, у чому полягає процеc зведення до першої зони Бриллюена.

9. Поясніть процес утворення енергетичних рівнів на прикладі атомів натрію.

10. Покажіть, як висновки про зонний характер енергії електронів у кристалі випливають із співвідношення невизначеностей Гейзенберга.

11. Зобразіть схематично зонну структуру металу, напівпровідника і діелектрика та поясніть розбіжності між ними.

12. Поясніть утворення енергетичного спектра електронів у кристалі на прикладі моделі Кроніга-Пенні.

13. Проаналізуйте, як змінюватиметься спектр електронів у граничному випадку: (наближення слабкого зв'язку).

14. Проаналізуйте, як змінюватиметься спектр електронів у граничному випадку: (наближення сильного зв'язку).

15. Яку величину називають ефективною масою електрона і з якою метою її ввели?

16. Виведіть загальну форму закону Ньютона для електрона в кристалі як квазічастинки.

17. Поясніть, яку поверхню називають ізоенергетичною.

18. Дайте визначення поверхні Фермі.

Розділ 4 електронна теорія металів

4.1 Класична електронна теорія металів

В основі електронної теорії металів лежить уявлення про електронний газ, що складається з вільних електронів (модель Друде). Електронному газу приписують властивості ідеального одноатобагато газу. Вільні електрони безперервно хаотично рухаються, причому середня кінетична енергія їх руху дорівнює . Вони обмінюються енергією з кристалічною решіткою при зіткненнях. Під дією зовнішнього електричного поля в металі виникає дрейф вільних електронів. Електрони прискорюються в проміжках між двома подальшими зіткненнями і передають при зіткненні отриману в електричному полі енергію кристалічній решітці. На основі цих уявлень можна пояснити ряд властивостей металів.

У проміжку між двома подальшими зіткненнями електрони під дією зовнішнього електричного поля рухаються з прискоренням , де - заряд електрона; E– напруженість електричного поля; m – маса електрона.

Максимальна швидкість електронів перед зіткненням дорівнює

,

де — середній час вільного пробігу електронів (час релаксації).

Середня швидкість дрейфу електронів дорівнює половині максимальної, оскільки відразу ж після зіткнення швидкість дрейфу електрона дорівнює нулю, а потім зростає з часом лінійно:

.

Підставивши даний вираз у формулу густини струму , отримаємо , тобто щільність струму в провіднику пропорційна напруженості електричного поля в ньому, а це є формулювання закону Ома. Таким чином, виведений закон збігається із знайденим експериментально. Множник є питомою електропровідністю металу. Якщо врахувати, що дрейфова швидкість електронів значно менша, ніж швидкість їх теплового руху, то час вільного пробігу електрона визначається так: , де - середня довжина вільного пробігу електрона; - середня швидкість його теплового руху. У класичній електронній теорії припускається, що дорівнює міжатомній відстані в кристалі. Отже, . Виведення цієї формули не можна вважати строгим, оскільки розглядався рух окремого «середнього» електрона, а отримані висновки поширювалися на всі вільні електрони. Правильнішим був би розгляд дії електричного поля на всю сукупність вільних електронів, причому їх сумарний імпульс змінюється під дією поля і зіткнень електронів їз решітками. Такий розгляд приводить до того, що середня дрейфова швидкість електронів виявляється удвічі більшою отриманої нами, і, отже, формула набере такого вигляду: . З цього виразу видно, що питома електропровідність металу залежить від природи металу (n і ) і від температури. Температурна залежність, яку дає електронна теорія, не відповідає експерименту, оскільки з дослідів відомо, що електропровідність змінюється приблизно обернено пропорційно до Т. Із останньої формули ніяк не випливає, що перехід металів у надпровідний стан повинен відбуватися стрибком при температурах вище за абсолютний нуль.

У електронній теорії металів можна вивести і деякі інші експериментальні закони. Наприклад, закон Відемана-Франца. Відкритий дослідним шляхом закон свідчить: відношення коефіцієнта теплопровідності металу до його питомої електропровідності однакове для всіх металів при однаковій температурі.

Таким чином, у випадку законів Ома, Відемана-Франца, Джоуля-Ленца електронна теорія дає задовільну якісну узгодженість з експериментом. Але електронна теорія приводить до значної розбіжності з дослідними даними при поясненні ряду важливих властивостей металів. Прикладом цього може слугувати величина молярної теплоємності металів. Згідно з електронною теорією вільні електрони металу обмінюються енергією при зіткненнях із кристалічною решіткою, і тому молярна теплоємність металу C_ повинна складатися з теплоємності кристалічної решітки C_v і теплоємності електронного газу C_ел, а саме: C_=C_v+C_ел.

Теплоємність кристалічної решітки за законом Дюлонга і Пті дорівнює C_v=3R. Припускаючи, що число вільних електронів в металі дорівнює числу атомів і що електрони мають три ступені вільності, отримаємо C_ел=3/2R. Молярна теплоємність металу повинна дорівнювати C_=9/2R. У той самий час для діелектриків, у яких немає вільних електронів, молярна теплоємність дорівнює 3R. Але дослід показує, що молярні теплоємності металів і діелектриків істотно не відрізняються. Електронна теорія металів ніяк не пояснює і залежність теплоємності металів від температури. Обмеженість класичної електронної теорії металів є наслідком того, що вона розглядає вільні електрони як класичні частинки, а сукупність їх електронний газ - як класичний ідеальний газ.