Методичнi рекомендації

У процесі вивчення цього розділу передусім необхідно запам’ятати, яке навантаження називається статичним; розібратися, як виражається робота зовнішніх статично прикладених сил через їхні значення і відповідні переміщення. Необхідно з’ясувати, як цю роботу можна виразити через згинальний момент M, поперечну Q і нормальну N сили. Слід звернути увагу на теореми про взаємність робіт і взаємність переміщень. Особливу увагу зосередити на застосуванні формули Мора для визначення переміщень пружних систем. Необхідно здобути практичні навички під час використання правила Верещагіна.

Запитання для самоперевiрки

1. Як виражається робота зовнішніх статично прикладених сил через значення цих сил і відповідні переміщення?

2. Як виражається робота зовнішніх статично прикладених сил через зусилля M, Q і N, які виникають у поперечних перерізах стержнів системи?

3. Як формулюється теорема про взаємність робіт? Доведіть цю теорему.

4. Як формулюється теорема про взаємність переміщень? Доведіть цю теорему.

5. Виведіть формулу переміщень (формулу Мора).

6. Що називається дійсним (або вантажним) і одиничним станом?

7. В якій послідовності визначають лінійні й кутові переміщення за формулою Мора?

8. Як перемножують епюри за правилом Верещагіна? Доведіть це правило.

9. Як за правилом Верещагіна перемножують епюри, обмежені ламаними лініями?

11. Статично невизначувані системи

11.1. Розрахунок рами методом сил

Побудуємо епюри М, Q і N для рами, зображеної на рис. 11.1. Для цієї рами , тобто рама два рази статично невизначувана.

Як приклад за основну систему візьмемо ламаний брус, закріплений правим кінцем. Будуємо одиничні й вантажні епюри згинальних моментів для основної системи (рис. 11.1). Напишемо канонічні рівняння методу сил:

Розрахуємо переміщення:

;

;

;

Рис. 11.1

При обчисленні переміщень були використані інтеграл Мора і правило Верещагіна.

Підставивши знайдені значення переміщень у канонічні рівняння і скоротивши на спільний множник , отримаємо:

, .

Розв’язавши цю систему рівнянь, знайдемо:

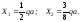
Переходимо до визначення згинальних моментів. У цьому випадку

.

Отже,

;

;

.

Розглянемо ригель АВ рами (рис. 11.2).

Для визначення згинального моменту між опорами А і В скористаємося формулою

(11.1)

В даному випадку ця формула має вигляд

;

Рис. 11.2

, звідки ;

.

Розглянемо стояк ВС (рис. 11.3). За формулою (11.1) знаходимо згинальний момент у перерізі під силою Р. Маємо:

.

Рис. 11.3

За одержаними даними будуємо епюру (рис. 11.1).

Для визначення поперечних сил використаємо формулу

Для ригеля АВ маємо:

Звідси при х = 0

при х = а .

Для стояка ВС (рис. 11.3) маємо:

За отриманими даними будуємо епюру Q (рис. 11.1).

Для визначення поздовжніх сил скористаємося способом вирізання вузлів (рис. 11.4). Склавши рівняння рівноваги всіх сил, прикладених до вузла В, отримаємо:

Рис. 11.4

; ,

звідки

.

За одержаними даними будуємо епюру N (рис. 11.1).

Виконаємо статичну перевірку отриманих результатів. Перевіримо рівновагу всієї системи. Для цього відкинемо всі опори і замінимо їхній вплив на систему реакціями цих опор (рис. 11.5). Складемо рівняння рівноваги:

; ;

.

Рис. 11.5

Таким чином, умови рівноваги задовольняються.

Виконаємо деформаційну перевірку, для чого перемножимо кожну з одиничних епюр і на остаточну епюру М. На основі рівняня

маємо:

;

Отже, деформаційна перевірка також задовольняється. Під час обчислення переміщень і було застосовано правило Верещагіна, а також таблицю інтегралів Мора (табл. Дод. 5).