6.6. Розрахунок вала на згинання з крученням

Підібрати діаметр вала постійного перерізу (рис. 6.19, а). Для розрахунків використати теорію міцності потенціальної енергії формозмінення. Матеріал валу сталь марки 40Х . 800 МПа, 1,5.

Дані для розрахунку:

Сила _{Р = 12 кН}; вага шківів і зубчастого колеса:

G₁ = 1,0 кН; G₂ = 0,75 кН; G₃ = 0,5 кН; діаметри: D₁ = 40 см; D₂ = 30 см; D₃ = 25 см; = 30;

Розв’язання.

1. Визначаємо значення сили Р₁. Для цього складаємо рівняння , де х поздовжня вісь вала. Маємо:

Підставляючи в це рівняння числові значення і 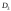, отримаємо:

.

Звідси 12,5 кН.

2. Будуємо епюру згинальних моментів , які діють у вертикальній площині. Сили , , , і переносимо паралельно самим собі до поздовжньої осі вала. Потім сили , і розкладаємо на вертикальні й горизонтальні складові. Вертикальні сили (), і ().

Маємо (рис. 6.19, б):

у перерізі С: = 1,5+ 1,0 = 10 кН;

у перерізі D: = 0,75 кН;

у перерізі Е: = 1,5 12,5 + 0,5 = 19,25 кН.

Визначаємо вертикальні опорні реакці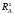ї і :

,

звідси = 2,75 кН;

Рис. 6.19

, ,

звідси =27,25 кН.

Перевірка:

;

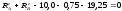2,75 + 27,25 30 = 0, 0 = 0.

Розрахуємо згинальні моменти для поперечних перерізів А, В, С, D, Е, ;

кНм;

кНм;

кНм; .

За цими даними будуємо епюру (рис. 6.19, в).

3. Будуємо епюру згинальних моментів , які діють у горизонтальній площині. Маємо такі горизонтальні сили (рис. 6.19, г):

у перерізі С: = 1,5 = 18 0,866 = 15,59 кН;

у перерізі D; 1,1Р = 1,1 = 13,2 кН.

Визначаємо горизонтальні опорні реакці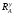ї і :

звідси = 14,88 кН;

звідси = 13,91 кН.

Перевірка:

14,88 + 13,91 28,79 = 0; 28,79 28,79 = 0; 0 = 0.

Визначаємо згинальні моменти для поперечних перерізів А, В, С, D, Е:

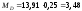кНм;

кНм; .

За цими даними будуємо епюру (рис. 6.19, д).

4. Будуємо епюру повних згинальних моментів М. Повний згинальний момент у будь-якому поперечному перерізі вала може бути визначений за формулою

.

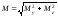Для поперечних перерізів А, В, С, D, Е. Маємо:

кНм;

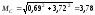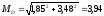кНм;

кНм; .

За отриманими даними будуємо епюру повних згинальних моментів М (рис. 6.19, е). Площини дії цих моментів у різних перерізах вала різні, але відповідні ординати епюри умовно сумісні з площиною рисунка. На тих ділянках вала, де прямі, які обмежують епюри і , перетинають осі епюр у точках, розташованих на одній вертикалі, епюра М обмежена прямими, а на решті ділянок вона обмежена кривими (рис. 6.19, е).

5. Будуємо епюру крутних моментів М_к, яка при сумісній дії згинання і кручення будується так само, як і при чистому крученні.

У перерізах С і Е, де розташовані шківи, і в перерізі D, де насаджено зубчасте колесо, слід прикласти зовнішні скручувальні моменти. Маємо:

кНм;

кНм.

Ці скручувальні моменти прикладаємо в перерізах С, D і Е вала (рис. 6.19, ж). За цими даними будуємо епюру крутних моментів М_к, (рис. 6.19, з).

6. Визначаємо небезпечний переріз вала, який встановлюється на основі епюр М і М_к. У цьому випадку небезпечним буде переріз D при х = 0,6 – 0. У цьому перерізі

М = 3,94 кНм; М_к = 1,20 кНм.

7. Знаходимо діаметр вала. Умова міцності при сумісному згинанні і крученні за четвертою теорією міцності має вигляд:

.

Тут – розрахункове напруження за четвертою теорією міцності; – розрахунковий (приведений) момент за четвертою теорією міцності; W осьовий момент опору поперечного перерізу вала; – допустиме напруження.

Отже,

.

За цією формулою можна розрахувати діаметр вала. Спочатку знаходимо:

кНм;

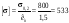МПа.

Таким чином,

м³ = 7,65 см³.

Для вала круглого поперечного перерізу

,

де r радіус вала; d діаметр вала.

Отже,

см.

Візьмемо остаточно d = 4,30 см.