Алгоритм построения сау с последовательными корректирующими звеньями

1. Задаемся желаемой логарифмической характеристикой.

2. Определяем ЛАЧХ объекта.

3. Получаем ЛАЧХ корректирующего звена, как разницу между ЛАЧХ желаемой и ЛАЧХ объекта.

4. Аппроксимируем ЛАЧХ дробно-рациональной функцией или полиномом.

5. По специальным таблицам получаем схему корректирующего звена (как правило, это RC - цепи).

Синтез сау с параллельными корректирующими устройствами

К

орректирующим звеном обычно охватывают ту часть объекта, которая имеет наибольший коэффициент усиления (в целях экономии).

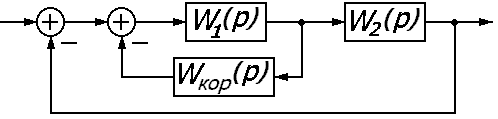
Рассмотрим , или в частотном виде

и тогда разомкнутую систему можно упростить за счет приведенных допущений

.

Если построить ЛАЧХ, то получим

.

Считая, что - желаемая ЛАЧХ, получим для корректирующего звена:

.

Иногда на практике возникает необходимость построения САУ комбинированной с последовательными и параллельными корректирующими звеньями.

Структурная схема такой САУ:

Считаем, что единицей в знаменателе можно пренебречь, тогда

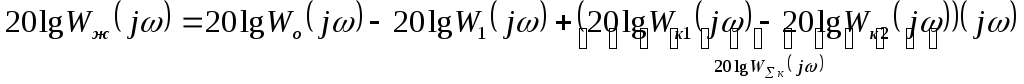
В результате синтеза мы получаем суммарную ЛАЧХ последовательного и параллельного корректирующего звена. Для разбиения этой ЛАЧХ на последовательные и параллельные дополнительные части проводятся дополнительные исследования.

Модальный регулятор.

Является методом корневого синтеза, а именно, по желаемому расположению корней характеристического уравнения на комплексной плоскости строится модальный регулятор, который представляет собой коэффициенты отрицательной обратной связи по каждой динамической переменной.

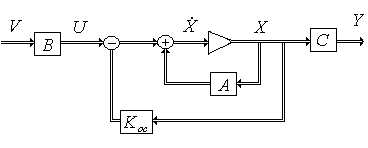
Дано описание объекта:

Задаёмся видом желаемого полинома D_жел(p) – в соответствии с заданными (желаемыми) показателями качества.

Введём обратную связь, вида:

где - характеристическое уравнение системы с регулятором.

Пример: Дана система уравнений

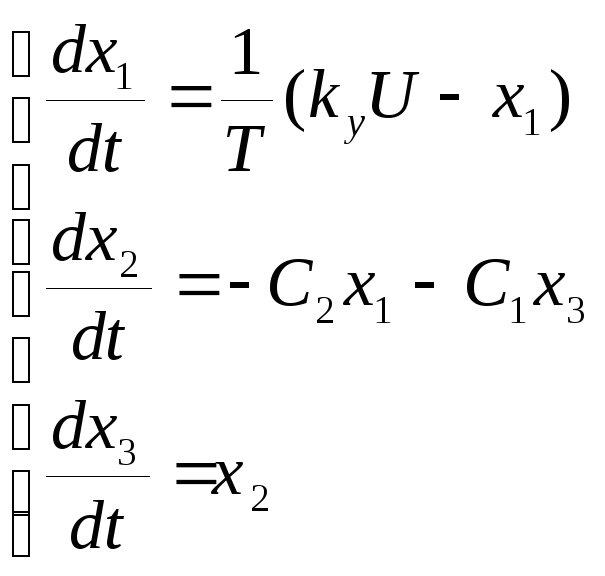
n₁ U x₁x₂x₃

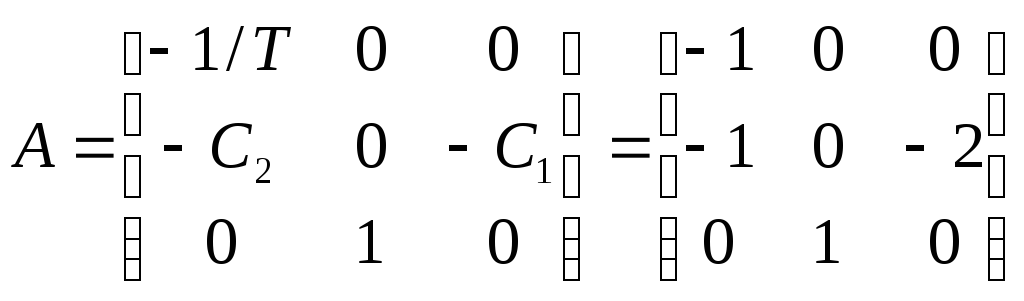
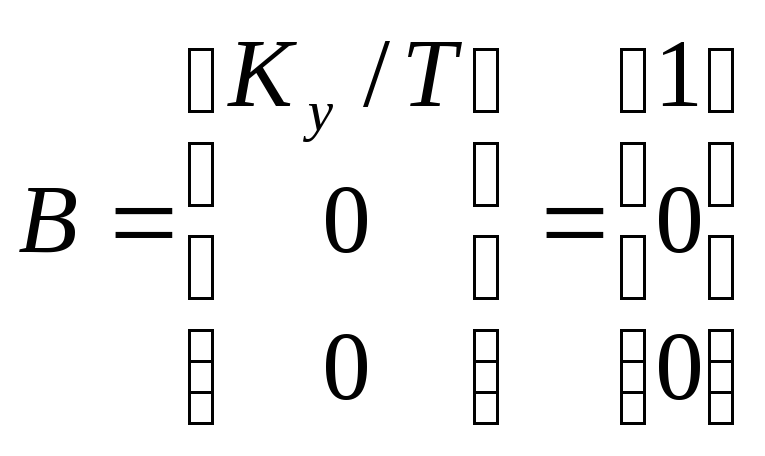
Нужно рассмотреть матрицу управляемости:

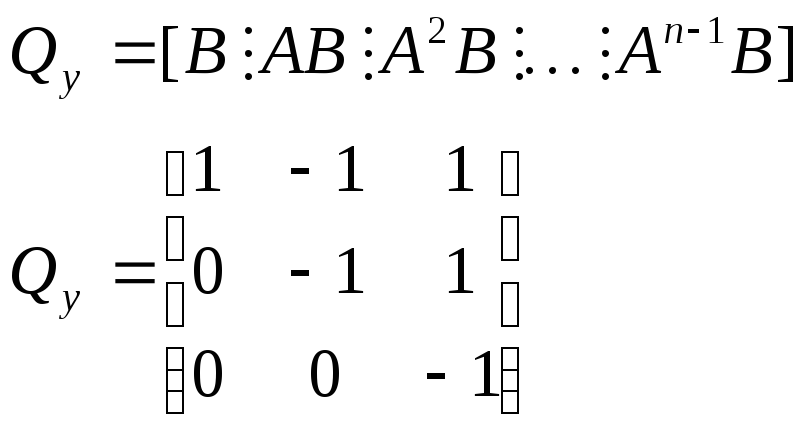Система управляема, так как ранг равен порядку системы

Выбираем желаемый полином той же степени, что и система:

D_жел(p)=(p+w₀)³=p³+3p²w₀+3pw₀₊w₀³

- оценка качества, где - время переходного процесса

При выбранном значении получаем:

K_oc1 = 2; K_oc2 = -1; K_oc3 =5;

Управляемость и наблюдаемость.

Система называется управляемой, если, изменяя любой из входных сигналов можно добиться желаемого значения на выходе системы за конечное время.

y₁

r₁

без нее система будет неуправляемой, а с ней -

управляемой.

Критерий управляемости.

Для того, чтобы система была управляемая необходимо и достаточно, чтобы ранг матрицы управляемости был равен n (порядок объекта).

В общем случае матрица управляемости является прямоугольной. Если система имеет один вход, то матрица имеет размерность .

Наблюдаемость.

Система называется наблюдаемой, если по выходным сигналам Y можно восстановить переменные состояния X.

Наблюдаемость, в отличие от измеряемости предполагает не только измерение переменных состояний X, а также вычисления не измеряемых переменных X по измеренным.

Измеряемость – это случай, когда непосредственно можно замерить любую переменную.

Критерий наблюдаемости.

Для того, чтобы система была наблюдаема необходимо и достаточно, чтобы ранг матрицы наблюдаемости был равен n (порядок объекта).

Дискретные системы автоматического управления

В дискретной системе управления один или несколько сигналов являются дискретными и представляют собой последовательность кратковременных импульсов. Обобщенная структурная схема дискретной САУ выглядит следующим образом:

З

десьr(t) – непрерывный управляющий сигнал; e(t) – непрерывный сигнал ошибки; m(t) – управляющая последовательность импульсов; y(t) – непрерывный выходной сигнал; y_ос(t) – непрерывный сигнал обратной связи; ДЭ – дискретный элемент; НЧ – непрерывная часть.

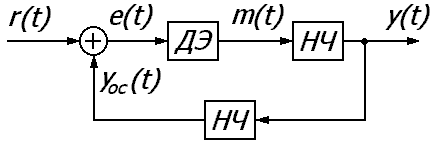
Типы дискретизации (квантования) сигналов

В состав дискретной системы наряду со звеньями непрерывного действия входят элементы, преобразующие непрерывные сигналы в дискретные, и элементы, выполняющие обратное преобразование. Преобразование непрерывного сигнала в дискретный называется квантованием. Различают три вида квантования сигналов: по уровню; по времени; по уровню и времени (совместно).

1

.Квантование сигнала по уровню заключается в фиксации вполне определенных дискретных значений непрерывного сигнала. При этом непрерывный сигнал (тонкая линия) заменяется ступенчато изменяющимся сигналом (жирная линия). Смежные дискретные значения отличаются друг от друга на постоянную величину ∆х, называемую интервалом квантования по уровню. Переход с одного уровня на другой происходит в моменты времени, когда непрерывный сигнал достигает очередного фиксированного значения.

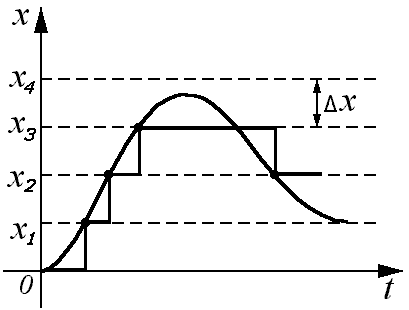
Системы автоматического управления, содержащие дискретный элемент, осуществляющий квантование по уровню, называются релейными системами, т.к. квантование по уровню производится специальными элементами – квантователями, простейшими из которых являются двух- и трехпозиционные реле. Они квантуют непрерывный сигнал соответственно по двум и трем уровням.

2

.Квантование по времени заключается в фиксации мгновенных значений непрерывного сигнала в равноотстоящие друг от друга дискретные моменты времени. При этом квантованный по времени сигнал представляет собой иак называемую решетчатую функцию – последовательность идеальных импульсов. Смежные моменты времени отличаются друг от друга на постоянную величину ∆t= T, называемую интер­валом дискретности (интервалом квантования по вре­мени, периодом повторения).

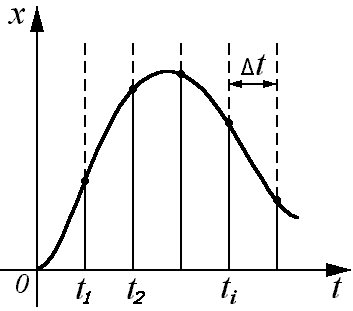
Квантование по времени осуществляется с помощью импульсного элемента. Импульсный элемент преобразует непрерывный входной сигнал в последовательность импульсов, амплитуда, длительность или период повторения которых зависят от значений входного сигнала в дискретные моменты времени. САУ, содержащие дискретный элемент, осуществляющий квантование по времени, называют дискретными (импульсными) САУ.

3. При совместном квантовании по времени и по уровню фиксируются дискретные по уровню значения, ближайшие к значениям непрерывного сигнала в дискретные моменты времени, причем приоритетным является квантование по времени.

Замена может осуществляться одним из четырех способов:

• ближайшее нижнее;

• ближайшее верхнее;

• среднее значение;

• ближайшее.

Сделаем замену по первому способу:

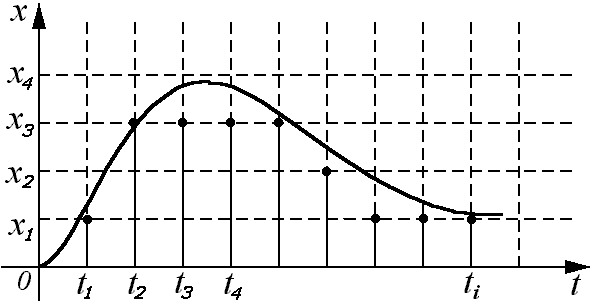
Дискретные системы, содержащие дискретный элемент, осуществляющий квантование по времени и по уровню, называются цифровыми системами автоматического управления.