Устойчивость систем сау

Устойчивость автоматической системы – это свойство системы возвращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему из этого состояния. Неустойчивая система не возвращается в исходное состояние, а непрерывно удаляется от него.

Здесь, в рисунке а), А₀ – невозмущенное состояние, А₂ – возмущенное состояние; на рисунке б) изображено неустойчивое состояние системы, а на рисунке в) – ее нейтральное состояние. По аналогии с состояниями можно ввести понятие возмущенного и невозмущенного движения.

Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением

где - свободная составляющая выходной величины системы.

Система является устойчивой, если свободная составляющая x_c(t) переходного процесса с течением времени стремится к нулю, т.е. если

.

Такая устойчивость называется асимптотической.

Если свободная составляющая неограниченно возрастает, т.Е. Если

,

то система неустойчива.

Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости.

Найдем общее условие, при котором система, описываемая уравнением (*), устойчива. Решение уравнения (*) равно сумме

где C_k – постоянные, зависящие от начальных условий; p_k – корни характеристического уравнения

.

Корни данного уравнения могут быть действительными (p_k=_k), мнимыми (p_k=j_k) и комплексными (p_k=_k± j_k).

П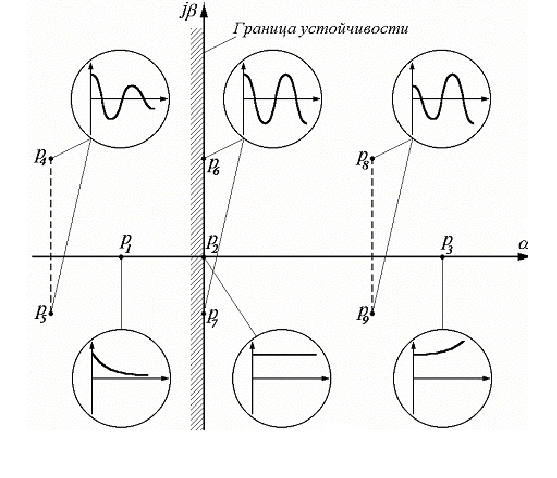ереходная составляющая (**) приt стремится к нулю лишь в том случае, если каждое слагаемое вида . Характер этой функции времени зависит от вида корняp_k. Рассмотрим все возможные случаи расположения корней p_k на комплексной плоскости (см. рис.) и соответствующие им функции x_k(t), которые показаны внутри кругов (как на экране осциллографа).

Рис.

1. Каждому действительному корню p_k=_k в решении (**) соответствует слагаемое вида

Если _k<0 (кореньр₁), то функция (***) приtстремится к нулю. Если_k>0 (кореньр₃), то функция (***) неограниченно возрастает. Если_k=0 (кореньр₂), то функция (***) остается постоянной.

2. Каждой паре сопряженных комплексных корней p_k=_k± j_k в решении (**) соответствуют два слагаемых, объединенных в одно

Эта функция представляет собой синусоиду с частотой _kи амплитудой, изменяющейся во времени по экспоненте. Если действительная часть двух комплексных корней_k<0 (корнир₄ир₅), то колебательная составляющая (****) будет затухать. Если_k>0 (корнир₈ир₉), то амплитуда колебаний будет неограниченно возрастать. Наконец, если_k=0 (корнир₆ир₇), т.е. если оба сопряженных корня – мнимые (p_k=+ j_k, p_k+1=- j_k), тоx_k(t)представляет собой незатухающую синусоиду с частотой_k.

Общее условие устойчивости:

Для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательны.

При этом действительные корни рассматриваются как частный случай комплексных корней, у которых мнимая часть равна нулю. Если хотя бы один корень имеет положительную действительную часть, то система будет неустойчивой.

Устойчивость системы зависит только от вида корней характеристического уравнения и не зависит от характера внешних воздействий на систему. Устойчивость есть внутреннее свойство системы, присущее ей вне зависимости от внешних условий.

Используя геометрическое представление корней на комплексной плоскости (см. рис.) в виде векторов или точек, можно дать вторую формулировку общего условия устойчивости (эквивалентную основной):

Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости. Если хотя бы один корень находится в правой полуплоскости, то система будет неустойчивой.

Мнимая ось j является границей устойчивости в плоскости корней. Если характеристическое уравнение имеет одну пару чисто мнимых корней (p_k=+j_k, p_k+1=-j_k), а все остальные корни находятся в левой полуплоскости, то в системе устанавливаются незатухающие гармонические колебания с круговой частотой . В этом случае говорят, что система находится наколебательной границе устойчивости.

Точка  =0 на мнимой оси соответствует так называемому нулевому корню. Если уравнение имеет один нулевой корень, то система находится на апериодической границе устойчивости. Если таких корня два, то система неустойчива.