лекции / lekciya_tau_kriterii_ustoychivosti_naykvista_gurvica_i_mihay

Лекция основы ТАУ

Критерии устойчивости Гурвица, Михайлова, Найквиста

Будем говорить, что линейная система устойчива, если ее реакция на любое ограниченное воздействие также ограничена, и неустойчива, если реакция на ограниченные воздействия неограниченна.

Необходимые условия устойчивости системы

Необходимым условием устойчивости системы является положительность коэффициентов характеристического уравнения. При наличии хотя бы одного отрицательного коэффициента система будет неустойчива. Положительность всех коэффициентов характеристического уравнения еще не гарантирует устойчивости системы, необходима ее дополнительная проверка.

На практике для упрощения расчетов устойчивость САУ определяют с помощью критериев устойчивости. Критерий устойчивости – это правила, позволяющие выяснить устойчивость системы без вычисления корней характеристического уравнения.

Рассматриваются коэффициенты характеристического уравнения или их функции.

Критерии устойчивости, позволяют по характеристическому уравнению или частотной характеристике определить, содержит ли передаточная функция полюса, находящиеся на мнимой оси в правой половине комплексной плоскости. Критерии устойчивости разделяют на алгебраические и частотные. К алгебраическим критериям относят критерий Гурвица, к частотным – Критерий Михайлова и Найквиста.

Критерий устойчивости Гурвица

Сформулирован математиком Гурвицем в 1895 г. Критерий Гурвица связывает расположение корней характеристического уравнения с определенными условиями, которые накладываются на его коэффициенты.

Запишем характеристической полином:

.

По правилу составляем матрицу Гурвица:

На главной диагонали сверху вниз выписываются по порядку коэффициенты характеристического уравнения от до включительно. В каждом столбце вниз по диагонали записываются коэффициенты при возрастающих степенях оператора , вверх – при убывающих степенях . Недостающие элементы дополняются нулями. В результате получим квадратную матрицу вида

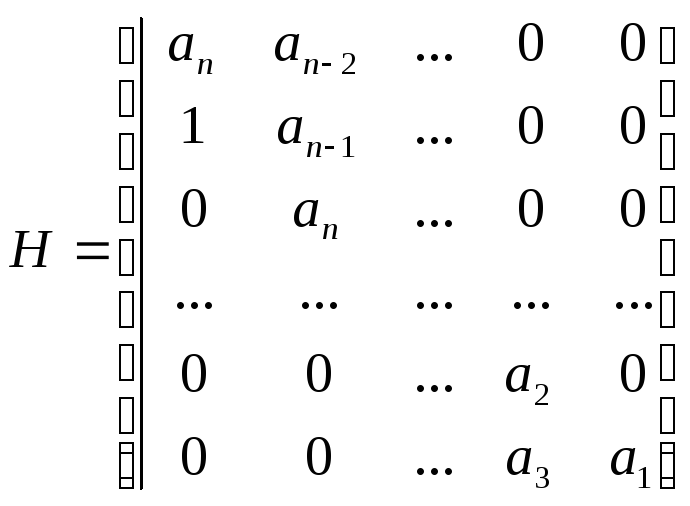
Где dimH = n*n.

Формулировка критерия. Для устойчивости линейной системы необходимо и достаточно, чтобы все n главных диагональных миноров матрицы Гурвица H, были положительными

,

Эти главные диагональные миноры называются определителями Гурвица. Они составляются следующим образом

,

…

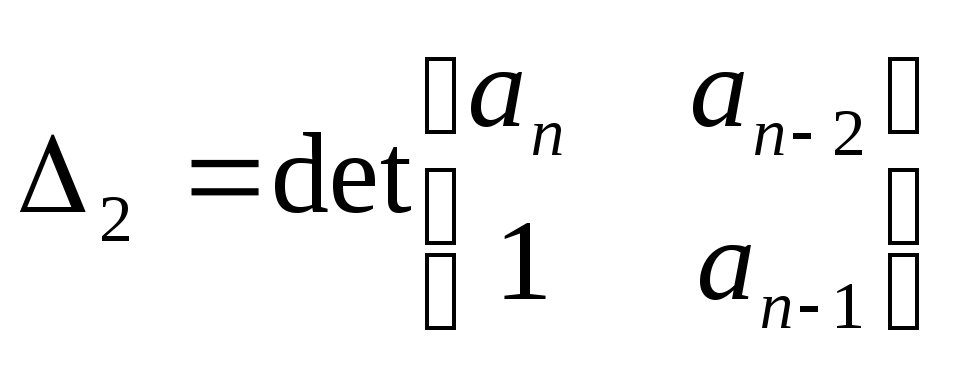
. Поскольку определить n-1 порядка должен быть положительным, последнее условие соответствует требованию .

Условием границы устойчивости является .

Пример: характеристический полином системы.

Построим матрицу Гурвица. Т.к. полином 4-й степени, матрица будет размером 4*4.

1) Рисуем диагональ, начиная со второго коэффициента полинома:

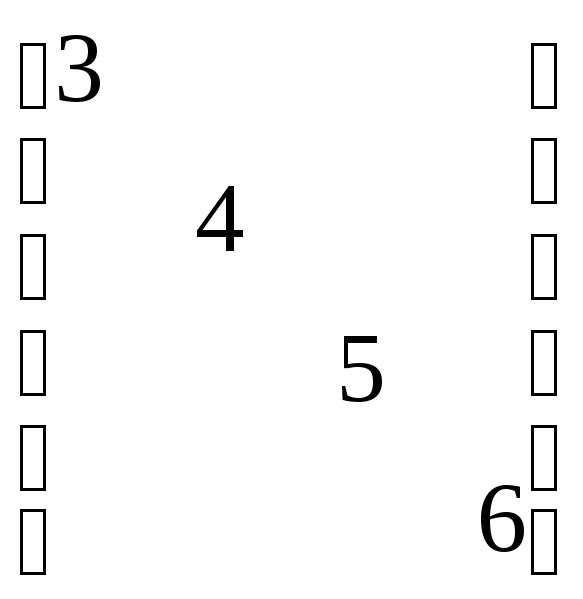
2) Дорисовываем первую строку матрицы, прыгая по коэффициентам через один:

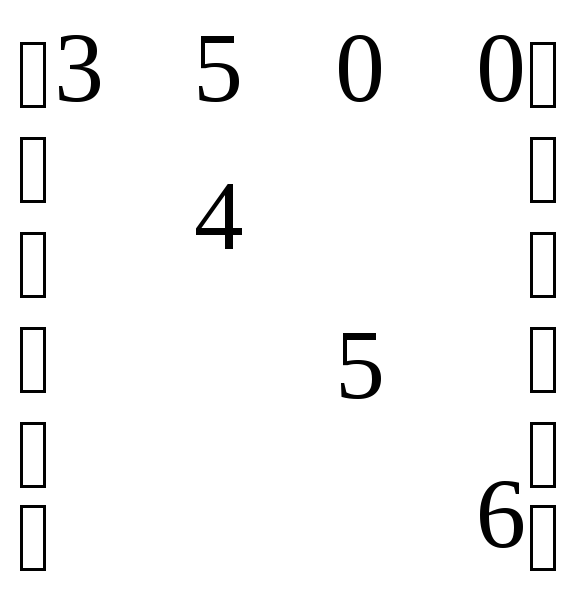
3)Дописываем столбцы, двигаясь от коэффициентов справа-налева:

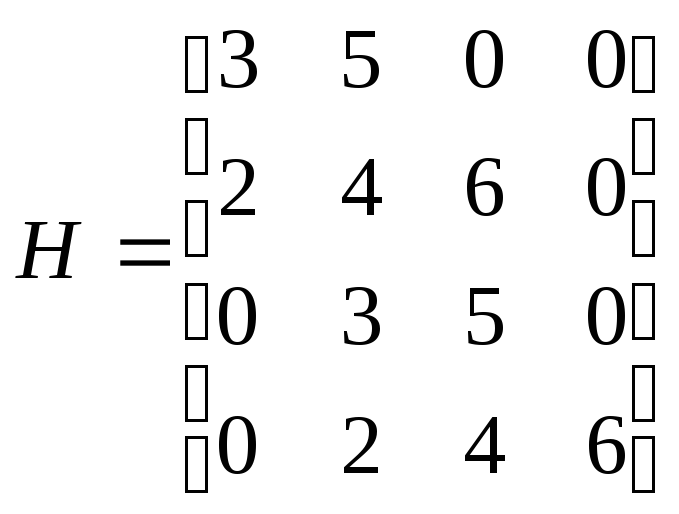
Система неустойчива.

Критерий устойчивости Михайлова.

Был сформулирован Михайловым в 1938 г., он базируется на принципе аргумента функции комплексной переменной.

Для анализа устойчивости системы предлагается исследовать характеристический комплекс , который получается из характеристического полинома

Заменой p на и имеет вид

Выделим мнимую и вещественную части, а также модуль и фазу:

При конкретном численном значении частоты характеристический комплекс представляет собой комплексное число , которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой

При изменении от 0 до конец вектора выписывает на комплексной плоскости некоторую кривую, которую называют годографом Михайлова. Причем начинается Причем начинается годограф в точке .

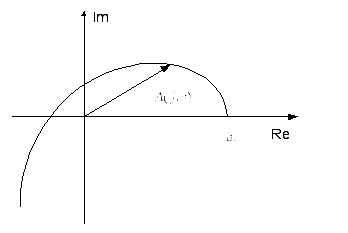
Формулировка критерия. Для устойчивости линейной системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от от 0 до начинался на вещественной оси в точке и проходил последовательно против часовой стрелки n квадрантов комплексной плоскости, не обращаясь в нуль и стремясь к в n-м квадранте.

Условием границы устойчивости является обращение в нуль годографа Михайлова при некотором значении частоты Аналитически это можно записать в виде

Здесь - частота незатухающих колебаний, возникающих в системе, которая находится на границе устойчивости.

Пример:

Проверить устойчивость системы, структурная схема которой приведена на рисунке.

И запишем ее характеристический полином

Перейдем к выражению годографа Михайлова

И представим его в форме

Построим таблицу при конкретных значениях частоты

	0	1	1,22	1,41	…
	3	1	0	-1	…	-
	0	1	0.61	0	…	-

По данным таблицы построим годограф Михайлова.

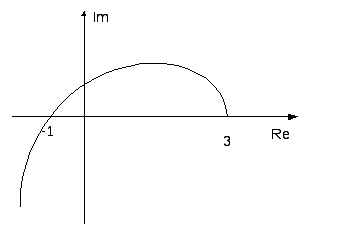
Годограф проходит последовательно три квадранта, не обращаясь в нуль и стремясь к бесконечности в третьем квадранте. Следовательно, система устойчива.

Критерий устойчивости Найквиста

Был разработан в 1932 г. Критерий Найквиста позволяет определить устойчивость системы с отрицательной обратной связью (замкнутой системы) по амплитудно-фазовой частотной характеристике разомкнутой системы.

Формулировка критерия Найквиста:

Для устойчивости системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении от 0 до не обхватывала току с координатами

Примеры расположения частотных характеристик, соответствующих устойчивой и неустойчивой замкнутым системам, представлены на рисунках.

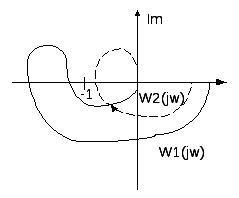
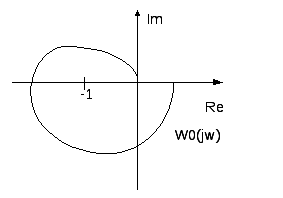
Устойчивые замкнутые системы Неустойчивая замкнутая системы.

Разомкнутая система может быть неустойчива, однако это не означает, что неустойчивой будет и замкнутая система. В этой ситуации стоит использовать видоизмененную формулировку критерия Найквиста: замкнутая система будет устойчива тогда и только тогда, когда амплитудно-фазовая характеристика неустойчивой разомкнутой системы при изменении от 0 до охватывает точку с координатами в положительном направлении r/2 раз, где r – число корней характеристического уравнения разомкнутой системы с положительной вещественной частью.

Критерий Найквиста можно также применять, если разомкнутая система имеет в своем составе интегратор, т.е. находится на границе устойчивости. В этом случае ее передаточную функцию можно записать в виде

Где - характеристический полином устойчивой системы.

Амплитудно-фазовая характеристика разомкнутой системы будет иметь неопределенность при : при этом амплитуда , а фаза скачком изменяется на 180’ . Для получения определенности характеристику при построении дополняют полуокружностью бесконечно большого радиуса так, чтобы она начиналась на положительной вещественной полуоси. Такое дополнение разомкнутой системы позволяет использовать формулировку критерия Найквиста.

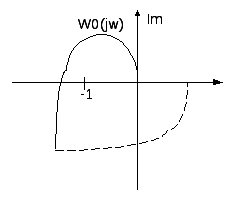
Сформулируем теперь условие устойчивости. Замкнутая система будет находится на границе устойчивости, если при некоторой частоте амплитудно-фазовая частотная характеристика разомкнутой системы проходит через точку с координатами .

Пример показан на рисунке

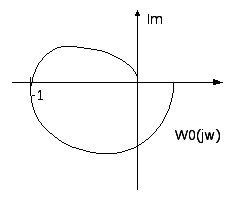
Критерий Найквиста можно применять и в общем случае, когда система содержит неединичную отрицательную обратную связь.

Пример.

Проверить устойчивость системы управления с помощью критерия Найквиста.

Разорвем обратную связь и определим передаточную функцию разомкнутой системы.

.

Согласно критерию Гурвица, разомкнутая система устойчива. Перейдем теперь к выражению для амплитудно-фазовой частотной характеристики

И выделим ее вещественную и мнимую части

Построим амплитудно-фазовую частотную характеристику разомкнутой системы, изменяя от 0 до .

	0	0,5	2
	0	-16/3	0	0
	10	0	-2/3	0

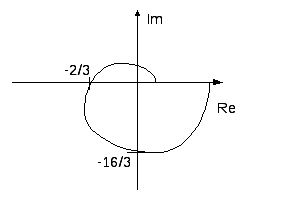
Амплитудно-фазовая характеристика разомкнутой системы не охватывает точку

, следовательно, замкнутая система устойчива.

Логарифмическая форма критерия Найквиста

Для проверки устойчивости замкнутой системы можно использовать логарифмические частотные характеристики разомкнутой системы.

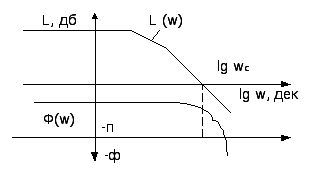
Формулировка критерия Найквиста. Для устойчивости замкнутой системы необходимо и достаточно, чтобы на всех частотах, где ЛАЧХ разомкнутой системы положительная () , фазовый сдвиг не достигал значения -180’ или достигал его четное число раз.

Рис

Замкнутая система будет находится на границе устойчивости, если на той же частоте , где ЛАЧХ системы обращается в нуль , значение фазовой частотной характеристики равно .