
- •Основы теории управления
- •Историческая справка
- •Основные понятия и определения тау
- •Структурные схемы
- •Пример типовой функциональной схемы сау
- •Детектирующие свойства элементов систем
- •Математическое описание сау
- •Уравнения динамики и статики
- •Линеаризация
- •Методология математического описания сау
- •Классификация сау
- •1. Классификация по характеру динамических процессов в системе
- •1.1. По виду сигналов, протекающих по контуру системы.
- •1.2. По виду дифференциальных уравнений.
- •1.3. По условиям функционирования.
- •2. Классификация по характеристикам управления
- •2.1. По принципу управления.
- •2.2. По режимам функционирования.
- •2.3. По свойствам системы в установившемся режиме.
- •3. Классификация сау по другим признакам
- •Основные (типовые) управляющие воздействия сау
- •Принцип суперпозиции для линейных систем
- •Временные характеристики сау
- •Переходные характеристики h(t) и (t) называют временными.
- •Передаточной функцией w(p) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях:
- •Частотные динамические характеристики
- •Классификация звеньев. Типовые динамические звенья
- •Апериодическое звено
- •Существует так называемое неустойчивое апериодическое звено
- •Колебательное звено
- •Общие свойства статических звеньев
- •Интегрирующие звенья
- •Идеальное интегрирующее звено
- •Реальное интегрирующее звено
- •Общие свойства интегрирующих звеньев
- •Изодромное интегрирующее звено
- •Идеальное дифференцирующее звено
- •Реальное дифференцирующее звено
- •Структурные преобразования схем сау
- •Типовые элементы структурных схем сау
- •Многоконтурные структурные схемы
- •Некоторые правила структурных преобразований
- •Изображение структурных схем в виде графов
- •Векторно-матричная форма описания многомерных элементов
- •Способ описания вход-выход
- •В общем случае каждая входная переменная связана с каждой выходной переменной. Если взаимосвязи по всем каналам линейны (линеаризованы), то в общем случае элемент можно описать следующей системой:
- •Описание сау методом пространства состояния
- •Схемы переменных состояний (спс)
- •Метод прямого программирования (базовый)
- •Методы последовательного и параллельного программирования
- •Схемы переменных состояния типовых звеньев
- •Связь между описанием “вход-выход” и мпс
- •Матрица перехода. Аналитический способ получения матрицы перехода
- •Получение изображения матрицы перехода по схеме переменных состояния
- •Получение матрицы перехода разложением в ряд
- •Устойчивость систем сау
- •Если свободная составляющая неограниченно возрастает, т.Е. Если
- •Алгебраические критерии устойчивости
- •Критерий Гурвица. Автоматическая система, описываемая характеристическим уравнением
- •Критерий Рауса.
- •Частотные критерии устойчивости
- •Принцип аргумента. Рассмотрим уравнение:
- •Критерий Михайлова Рассмотрим характеристическое уравнение системы
- •Критерий Найквиста
- •У замкнутой системы изменение аргумента при изменении частоты от 0 до :
- •Система неустойчивая.
- •Запас устойчивости Запас устойчивости по алгебраическому критерию Гурвица
- •Запас устойчивости при частотных критериях устойчивости
- •Устойчивость систем со звеном чистого запаздывания
- •Влияние параметров на устойчивость системы.
- •Структурно устойчивые и структурно неустойчивые системы
- •Влияние структуры и передаточного коэффициента системы на устойчивость
- •Рассмотрим влияние передаточного коэффициентасистемы на устойчивость. Учтём, что для одноконтурных систем коэффициентkвходит в выражение для афчх как множитель:
- •Анализ качества сау
- •Основные (прямые) показатели качества сау
- •Прямые методы оценки качества (методы построения переходной характеристики)
- •Операторный метод:
- •2. Частотный метод.
- •Понятие обобщенной частотной передаточной функции
- •3. Моделирование с использованием вычислительных средств
- •Косвенные методы оценки показателей качества сау
- •Корневые методы оценки показателей качества
- •Смещенные уравнения
- •Влияние нулей передаточной функции на качество переходного процесса
- •Диаграмма Вышнеградского
- •Частотные методы Приближенное определение показателей качества по виду р() (Косвенный метод)
- •О тбрасываемая часть при частотах свышеПвлияет на начало переходной характеристикиh(t).
- •Построение вещественной частотной характеристики с использованием
- •Линейная интегральная оценка
- •Метод Кулебакина
- •Модульная интегральная оценка
- •Квадратичная интегральная оценка
- •Апериодическая интегральная оценка
- •Рассмотрим передаточную функцию типовой одноконтурной системы
- •Тогда ошибка будет зависеть только от задающего воздействия
- •Ошибки статических и астатических систем при типовых задающих воздействиях
- •Ошибка при возмущающем воздействии, не равном нулю
- •Основные понятия о синтезе систем управления
- •Особенности синтеза
- •Этапы синтеза сау
- •Т иповые законы регулирования линейных систем
- •Коэффициенты характеристического полинома замкнутой системы, оптимальные по критерию ивмо.
- •Синтез систем методом лачх
- •Желаемая лачх
- •Построение желаемой лачх
- •Синтез последовательных корректирующих устройств
- •Алгоритм построения сау с последовательными корректирующими звеньями
- •Синтез сау с параллельными корректирующими устройствами
- •Модальный регулятор.
- •Управляемость и наблюдаемость.
- •Импульсные сау
- •М атематическое описание дискретной системы
- •Главное достоинство и удобство z-преобразования заключается в том, что сама запись z-изображения указывает простой способ выполнения прямого и обратного преобразования:
- •Свойства z-преобразования аналогичны свойствам обычного преобразования Лапласа. Приведем важнейшие из них.
- •Дискретная передаточная функция
- •Передаточная функция на основе разностных уравнений
- •Примеры типовых дискретно-непрерывных систем
- •Годографы вектора f(ejt) для устойчивой и неустойчивой системы второго порядка показаны на рисунке.
- •Описание дискретных систем в терминах пространства состояния
- •Метод прямого программирования
- •Метод переменного коэффициента усиления.
У замкнутой системы изменение аргумента при изменении частоты от 0 до :
![]() для
устойчивой системы
для
устойчивой системы
Изменение аргумента вспомогательной функции составит:
![]() .
.
Тогда критерий Найквиста звучит так:
если
система неустойчива в разомкнутом
состоянии и имеет m
положительных корней характеристического
уравнения, то система в замкнутом
состоянии будет устойчива лишь в том
случае, если годограф разомкнутой
системы охватывает точку (-1; ј0) в
положительном направлении m
раз, или, используя правило переходов:
разность между количеством положительных
переходов и количеством отрицательных
переходов отрезка
![]() действительной оси будет равна
действительной оси будет равна
![]() .
.
Объединяя два случая, можно дать следующее определение критерия Найквиста:
Система
в замкнутом состоянии будет устойчива,
если разность между числами положительных
и отрицательных переходов годографа
АФЧХ разомкнутой системы на отрезке
![]() действительной оси будет равна
действительной оси будет равна![]() ,
где т – количество правых корней
характеристического уравнения разомкнутой
системы.
,
где т – количество правых корней
характеристического уравнения разомкнутой
системы.
Если АФЧХ начинается или заканчивается на отрезке ( -∞; -1), то считают, что характеристика совершает полперехода.
Примеры:
1. т = 2

2

Система неустойчивая.
т=5
![]()
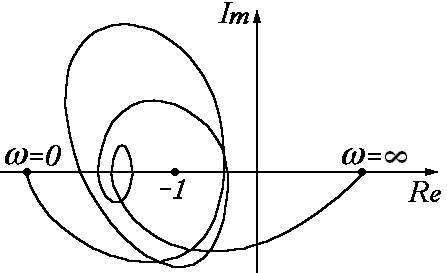
Критерий Найквиста для астатических систем
Для
определения устойчивости систем с
астатизмом порядка
![]() ,
следует дополнить АФЧХ разомкнутой
системы дугой
,
следует дополнить АФЧХ разомкнутой
системы дугой![]() окружности
бесконечно большого радиуса и затем
применить критерий Найквиста.
окружности
бесконечно большого радиуса и затем
применить критерий Найквиста.
Примеры.


Логарифмический критерий устойчивости
Логарифмический критерий устойчивости применяется при исследовании сложных многоконтурных систем, при построении ЛАЧХ корректирующих звеньев, выводящих исходную систему из неустойчивого состояния. Базовым для логарифмического критерия устойчивости является критерий Найквиста.
По критерию Найквиста, базовая точка (-1;0) в комплексной плоскости.
Пример 1.
Рассмотрим АФЧХ разомкнутой системы в двух случаях:
1. АФЧХ первого рода, когда система в разомкнутом состоянии устойчива.
С

Пример 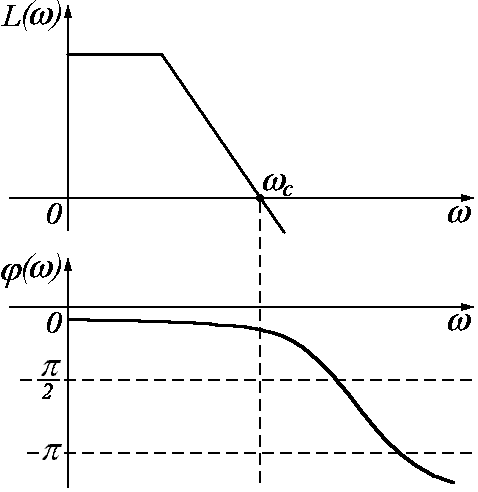 2.
2.
Но бывают АФЧХ другого вида, например, “клювообразные”:

Для них, как мы
видим, частота wП
< wср,
хотя замкнутая система будет устойчивой
(при устойчивой разомкнутой).
Пример 3.
Д

Для
АФЧХ второго рода логарифмический
критерий устойчивости заключается в
следующем (это общая
формулировка логарифмического критерия
Найквиста):
САУ в замкнутом
состоянии
будет
устойчива,
если при положительных значениях ЛАЧХ
разомкнутой системы разность между
количеством положительных и отрицательных
переходов фазочастотной характеристики
через прямые
![]() (k=1,3,5,…)
будет равно
(k=1,3,5,…)
будет равно
![]() .
.
При
этом для астатических систем также, как
и при анализе АФЧХ, потребуются
дополнительные построения: начальный
участок фазочастотной характеристики
следует дополнить на величину
![]() .
.
