Структурно устойчивые и структурно неустойчивые системы

Структурно устойчивой системой называется система, устойчивости которой можно добиться, изменяя параметры звеньев, при этом тип звеньев и их соединения остаются неизменными.

З

десьК_ОС – коэффициент обратной связи.

Устойчивость такой системы достигается путем изменения, например, коэффициентов усиления.

Структурно неустойчивой системой называется система, устойчивость которой может быть достигнута только после изменения структуры (замена типов звеньев или характеров соединений).

С

амим: убедиться в структурной неустойчивости данной системы.

Влияние структуры и передаточного коэффициента системы на устойчивость

Существуют звенья, которые, как правило, ухудшают устойчивость системы, и звенья, которые почти всегда улучшают устойчивость.

Ухудшают:

Идеально-интегрирующее (их количество обозначим q)

Неустойчивое апериодическое (их количество обозначим t)

Консервативное (их количество обозначим r)

Улучшают:

Форсирующие (обычно первого порядка)

Если форсирующих звеньев нет, то условие структурной устойчивости замкнутой системы:

Рассмотрим влияние передаточного коэффициентасистемы на устойчивость. Учтём, что для одноконтурных систем коэффициентkвходит в выражение для афчх как множитель:

Это означает, что длина вектора W(jw) при всех значениях w пропорциональна k. При увеличении k АФЧХ расширяется и приближается к критической точке. Следовательно, увеличение передаточного коэффициента разомкнутого контура приводит к нарушению устойчивости.

Это правило справедливо для большинства реальных систем, у которых АФЧХ имеет форму плавной спирали. Но для клювообразных систем к нарушению устойчивости приводит не только увеличение, но и уменьшение k.

Значение передаточного коэффициента, при котором АФЧХ проходит через точку (-1; 0) называется предельным, или критическим.

Рассмотрим критерий Михайлова. У простых одноконтурных ситем k входит только в коэффициент a_n характеристического уравнения, причём

Если k возрастает, то будет возрастать только a_n, а характеристическая кривая D(jw) без деформации будет перемещаться вправо.

Таким образом, установлена одна из важнейших в ТАУ закономерностей:

Чем больше общий передаточный коэффициент разомкнутого контура, тем ближе замкнутая система к границе устойчивости.

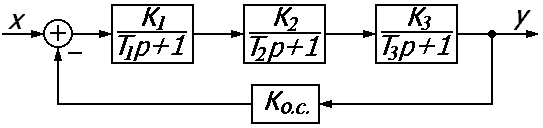
Предельное значение коэффициента k зависит от соотношения постоянных времени звеньев. Например, система из трёх апериодических звеньев:

- передаточная функция разомкнутого контура.

Характеристическое уравнение всей системы:

где

по критерию Гурвица при границе устойчивости:

решим это уравнение относительно k_кр, разделив на , получим:

Анализируя это уравнение, видим, что предельный коэффициент тем больше, чем больше разность между двумя наиболее различающимися постоянными времени, и чем ближе третья постоянная времени к среднеарифметическому значения двух первых.

Эта закономерность справедлива для систем любого порядка.

Получаем важное практическое правило:

Предельное значение передаточного коэффициента системы зависит от соотношения постоянных времени и не зависит от их абсолютных значений.