
- •Основы теории управления
- •Историческая справка
- •Основные понятия и определения тау
- •Структурные схемы
- •Пример типовой функциональной схемы сау
- •Детектирующие свойства элементов систем
- •Математическое описание сау
- •Уравнения динамики и статики
- •Линеаризация
- •Методология математического описания сау
- •Классификация сау
- •1. Классификация по характеру динамических процессов в системе
- •1.1. По виду сигналов, протекающих по контуру системы.
- •1.2. По виду дифференциальных уравнений.
- •1.3. По условиям функционирования.
- •2. Классификация по характеристикам управления
- •2.1. По принципу управления.
- •2.2. По режимам функционирования.
- •2.3. По свойствам системы в установившемся режиме.
- •3. Классификация сау по другим признакам
- •Основные (типовые) управляющие воздействия сау
- •Принцип суперпозиции для линейных систем
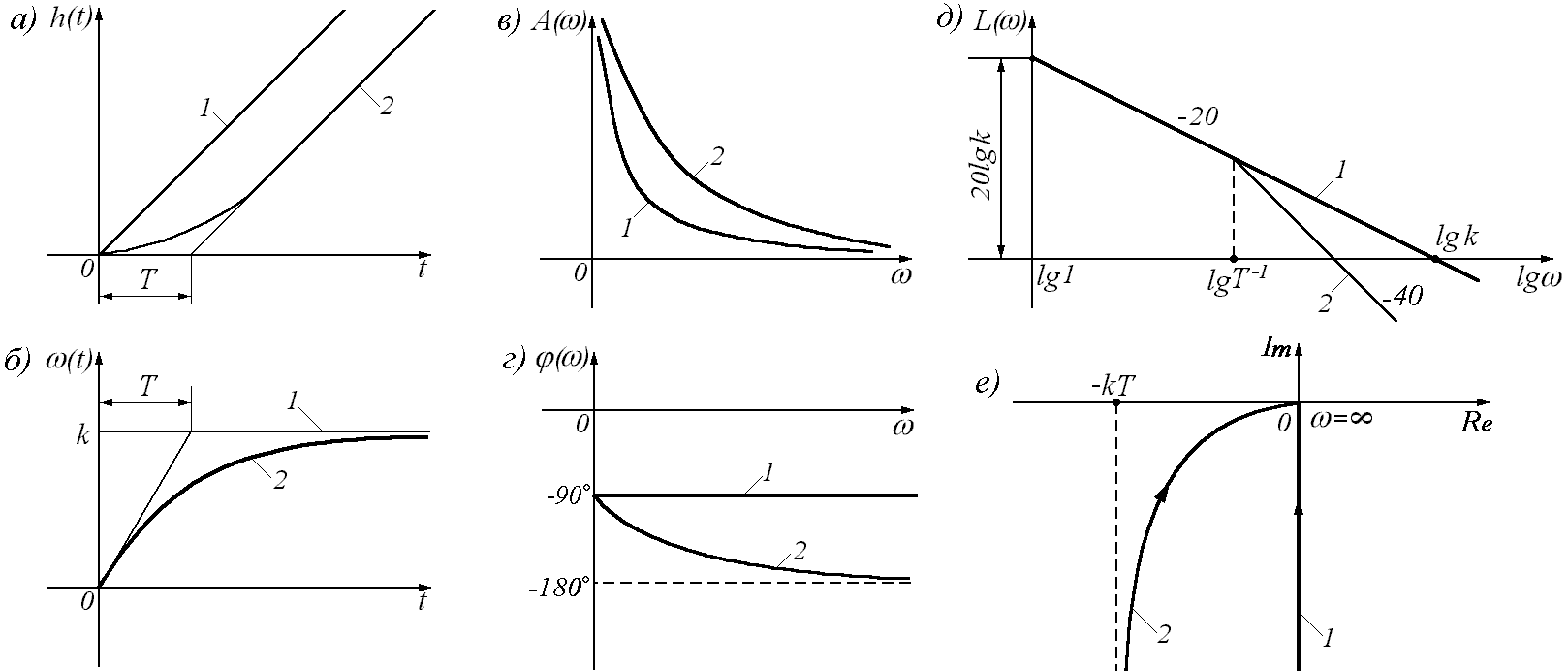
- •Временные характеристики сау
- •Переходные характеристики h(t) и (t) называют временными.
- •Передаточной функцией w(p) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях:
- •Частотные динамические характеристики
- •Классификация звеньев. Типовые динамические звенья
- •Апериодическое звено
- •Существует так называемое неустойчивое апериодическое звено
- •Колебательное звено
- •Общие свойства статических звеньев
- •Интегрирующие звенья
- •Идеальное интегрирующее звено
- •Реальное интегрирующее звено
- •Общие свойства интегрирующих звеньев
- •Изодромное интегрирующее звено
- •Идеальное дифференцирующее звено
- •Реальное дифференцирующее звено
- •Структурные преобразования схем сау
- •Типовые элементы структурных схем сау
- •Многоконтурные структурные схемы
- •Некоторые правила структурных преобразований
- •Изображение структурных схем в виде графов
- •Векторно-матричная форма описания многомерных элементов
- •Способ описания вход-выход
- •В общем случае каждая входная переменная связана с каждой выходной переменной. Если взаимосвязи по всем каналам линейны (линеаризованы), то в общем случае элемент можно описать следующей системой:
- •Описание сау методом пространства состояния
- •Схемы переменных состояний (спс)
- •Метод прямого программирования (базовый)
- •Методы последовательного и параллельного программирования
- •Схемы переменных состояния типовых звеньев
- •Связь между описанием “вход-выход” и мпс
- •Матрица перехода. Аналитический способ получения матрицы перехода
- •Получение изображения матрицы перехода по схеме переменных состояния
- •Получение матрицы перехода разложением в ряд
- •Устойчивость систем сау
- •Если свободная составляющая неограниченно возрастает, т.Е. Если
- •Алгебраические критерии устойчивости
- •Критерий Гурвица. Автоматическая система, описываемая характеристическим уравнением
- •Критерий Рауса.
- •Частотные критерии устойчивости
- •Принцип аргумента. Рассмотрим уравнение:
- •Критерий Михайлова Рассмотрим характеристическое уравнение системы
- •Критерий Найквиста
- •У замкнутой системы изменение аргумента при изменении частоты от 0 до :
- •Система неустойчивая.
- •Запас устойчивости Запас устойчивости по алгебраическому критерию Гурвица
- •Запас устойчивости при частотных критериях устойчивости
- •Устойчивость систем со звеном чистого запаздывания
- •Влияние параметров на устойчивость системы.
- •Структурно устойчивые и структурно неустойчивые системы
- •Влияние структуры и передаточного коэффициента системы на устойчивость
- •Рассмотрим влияние передаточного коэффициентасистемы на устойчивость. Учтём, что для одноконтурных систем коэффициентkвходит в выражение для афчх как множитель:
- •Анализ качества сау
- •Основные (прямые) показатели качества сау
- •Прямые методы оценки качества (методы построения переходной характеристики)
- •Операторный метод:
- •2. Частотный метод.
- •Понятие обобщенной частотной передаточной функции
- •3. Моделирование с использованием вычислительных средств
- •Косвенные методы оценки показателей качества сау
- •Корневые методы оценки показателей качества
- •Смещенные уравнения
- •Влияние нулей передаточной функции на качество переходного процесса
- •Диаграмма Вышнеградского
- •Частотные методы Приближенное определение показателей качества по виду р() (Косвенный метод)
- •О тбрасываемая часть при частотах свышеПвлияет на начало переходной характеристикиh(t).
- •Построение вещественной частотной характеристики с использованием
- •Линейная интегральная оценка
- •Метод Кулебакина
- •Модульная интегральная оценка
- •Квадратичная интегральная оценка
- •Апериодическая интегральная оценка
- •Рассмотрим передаточную функцию типовой одноконтурной системы
- •Тогда ошибка будет зависеть только от задающего воздействия
- •Ошибки статических и астатических систем при типовых задающих воздействиях
- •Ошибка при возмущающем воздействии, не равном нулю
- •Основные понятия о синтезе систем управления
- •Особенности синтеза
- •Этапы синтеза сау
- •Т иповые законы регулирования линейных систем
- •Коэффициенты характеристического полинома замкнутой системы, оптимальные по критерию ивмо.
- •Синтез систем методом лачх
- •Желаемая лачх
- •Построение желаемой лачх
- •Синтез последовательных корректирующих устройств
- •Алгоритм построения сау с последовательными корректирующими звеньями
- •Синтез сау с параллельными корректирующими устройствами
- •Модальный регулятор.
- •Управляемость и наблюдаемость.
- •Импульсные сау
- •М атематическое описание дискретной системы
- •Главное достоинство и удобство z-преобразования заключается в том, что сама запись z-изображения указывает простой способ выполнения прямого и обратного преобразования:
- •Свойства z-преобразования аналогичны свойствам обычного преобразования Лапласа. Приведем важнейшие из них.
- •Дискретная передаточная функция
- •Передаточная функция на основе разностных уравнений
- •Примеры типовых дискретно-непрерывных систем
- •Годографы вектора f(ejt) для устойчивой и неустойчивой системы второго порядка показаны на рисунке.
- •Описание дискретных систем в терминах пространства состояния
- •Метод прямого программирования
- •Метод переменного коэффициента усиления.
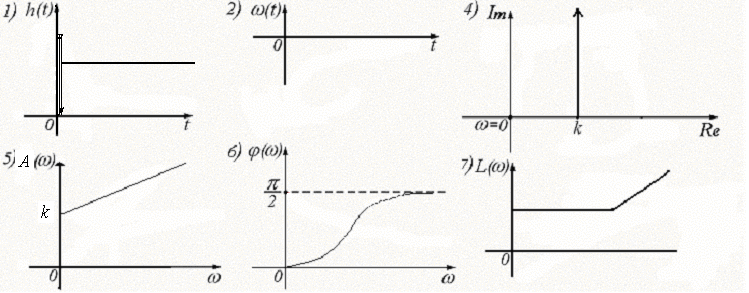
Реальное интегрирующее звено
Динамика процесса в таком звене описывается следующим уравнением:
![]() ,
,
где k – коэффициент усиления.
1. Переходная характеристика:
![]()
2. Импульсная переходная характеристика:
![]()
3. Передаточная функция реального интегрирующего звена:
![]()
![]()
![]()
Реальное интегрирующее звено представляет собой последовательное соединение идеального интегрирующего звена и апериодического.
4. АФЧХ:
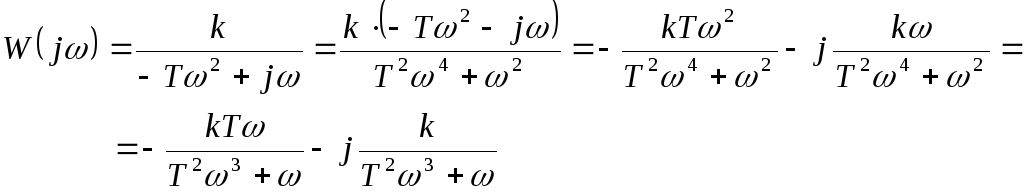
5. АЧХ:
![]()
6. ФЧХ:
![]()
7. ЛАЧХ:
![]()
С
![]()
Примером может служить электродвигатель постоянного тока, в котором управляемая величина – поворот вала двигателя.
Общие свойства интегрирующих звеньев
После подачи на вход ступенчатого воздействия, выходная переменная y(t) неограниченно возрастает и по окончании ПП изменяется по линейному закону
![]()
При
снятии входного воздействия выходная
переменная сохраняет достигнутое
значение
![]() интегрирующие
звенья можно использовать в качестве
запоминающих элементов.
интегрирующие
звенья можно использовать в качестве
запоминающих элементов.
Передаточный коэффициент звена связан с передаточной функцией соотношением
![]()
![]()
![]()
Звенья также являются фильтрами низкой частоты
Изодромное интегрирующее звено
Динамика процесса описывается следующим уравнением:
![]() ,
,
здесь k и k1 – коэффициенты усиления.
1. Переходная характеристика:
![]()
2. Импульсная переходная характеристика:
![]()
3. Передаточная функция:
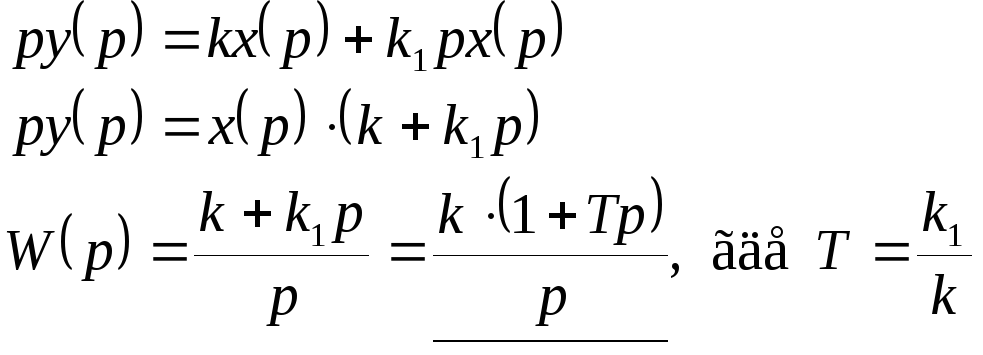
4. АФЧХ:
![]()
5. АЧХ:
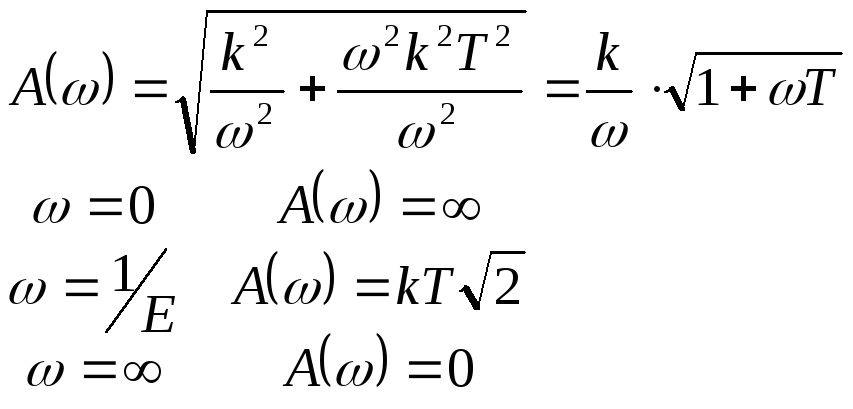
6. ФЧХ:
![]()
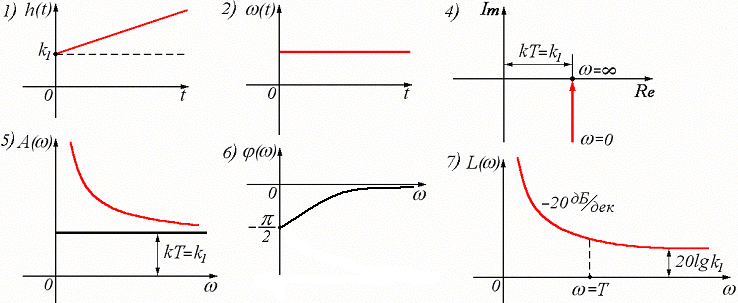 7.
ЛАЧХ:
7.
ЛАЧХ:
![]()
С
![]()
Идеальное дифференцирующее звено
Динамика процесса в таком звене описывается уравнением:
![]()
1. Переходная характеристика:
![]()
2. Импульсная переходная характеристика:

3. Передаточная функция:

4. АФЧХ:
![]()
совпадает с положительной частью мнимой оси.
5. АЧХ:
![]()
показывает: чем больше частота входного сигнала, тем больше амплитуда выходного сигнала. Эта особенность дифференцирующих звеньев вытекает непосредственно из основного уравнения: чем быстрее изменяется во времени сигнал x(t), тем больше его производная в правой части и выходной сигнал y(t).
6. ФЧХ:
Сдвиг фаз, создаваемый идеальным дифференцирующим звеном, на всех частотах одинаков и равен
![]()
7. ЛАЧХ звена:
![]()
-
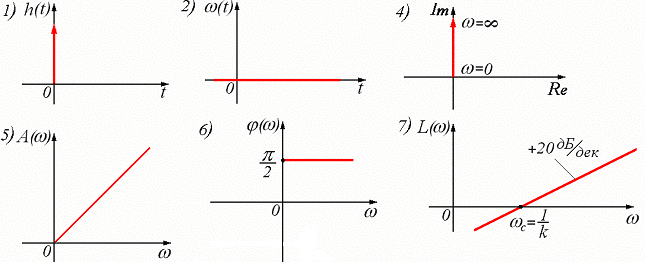
![]() .
.
С
![]()
Реальное дифференцирующее звено
Динамика дифференцирующего звена представлена уравнением
![]()
1. Переходная характеристика:
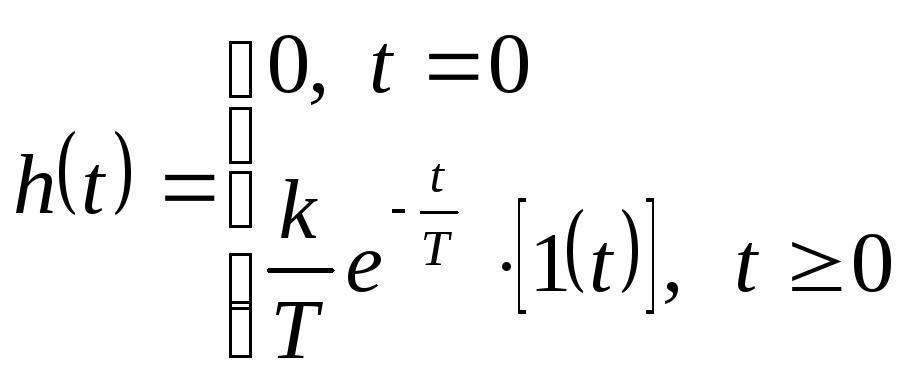
График меняется скачком.
2. Импульсная переходная характеристика:
![]()
3. Передаточная функция:
4. АФЧХ:
![]()
5. АЧХ:
![]()
6. ФЧХ:
![]()
7. ЛАЧХ:
![]()
С

![]()
Форсирующее звено
Динамика форсирующего звена представлена уравнением
![]()
1. Переходная характеристика:
![]()
2. Импульсная переходная характеристика:
![]()
3. Передаточная функция:
![]()
Можно представить как параллельное соединение безынерционного и идеального дифференцирующего звеньев.
4. АФЧХ:
![]()
5. АЧХ:
![]()
6. ФЧХ:
![]()
7. ЛАЧХ:
![]()
Также как и дифференцирующее звено, форсирующее звено в идеальном виде не может быть реализовано. В реальных форсирующих устройствах всегда имеются малые параметры, создающие инерционность.
Общие свойства дифференцирующих звеньев
При подаче на вход ступенчатого воздействия, на выходе возникает большой кратковременный импульс, а затем выход = 0.
Дифференцирующие звенья в статике не передают входной сигнал
![]()
![]()
![]()
Звенья являются фильтрами высокой частоты, вносят положительные фазовые сдвиги.
Реальное форсирующее звено (упругое)
Динамика упругого звена представлена уравнением
![]()
Передаточная функция
![]()
Существенным
параметром данного звена является
коэффициент![]() .
.
Если
![]() ,
то звено подобно апериодическому,
,
то звено подобно апериодическому,
если![]() ,
то звено подобно реальному дифференциальному
звену.
,
то звено подобно реальному дифференциальному
звену.
Форсирующее звено второго порядка
Передаточная функция
![]()
Если
![]() ,
то звено не относится к числу типовых,
его можно представить как последовательное
соединение двух форсирующих звеньев
первого порядка.
,
то звено не относится к числу типовых,
его можно представить как последовательное
соединение двух форсирующих звеньев
первого порядка.
Звено чистого запаздывания
Примеры - конвейеры, трубопроводы.
Звеном чистого запаздывания называется такое звено, выходная величина которого полностью повторяет входную величину, но со сдвигом во времени на величину (время запаздывания).
Д

![]() ,
,
где - длительность запаздывания.
1. Переходная характеристика:
![]()
2. Импульсная переходная характеристика:
![]()
3. Передаточная функция звена:
![]()
4. АФЧХ:
![]()
представляет собой окружность с центром в начале координат и радиусом, равным единице.
5. АЧХ:
![]()
6. ФЧХ:
![]()
7
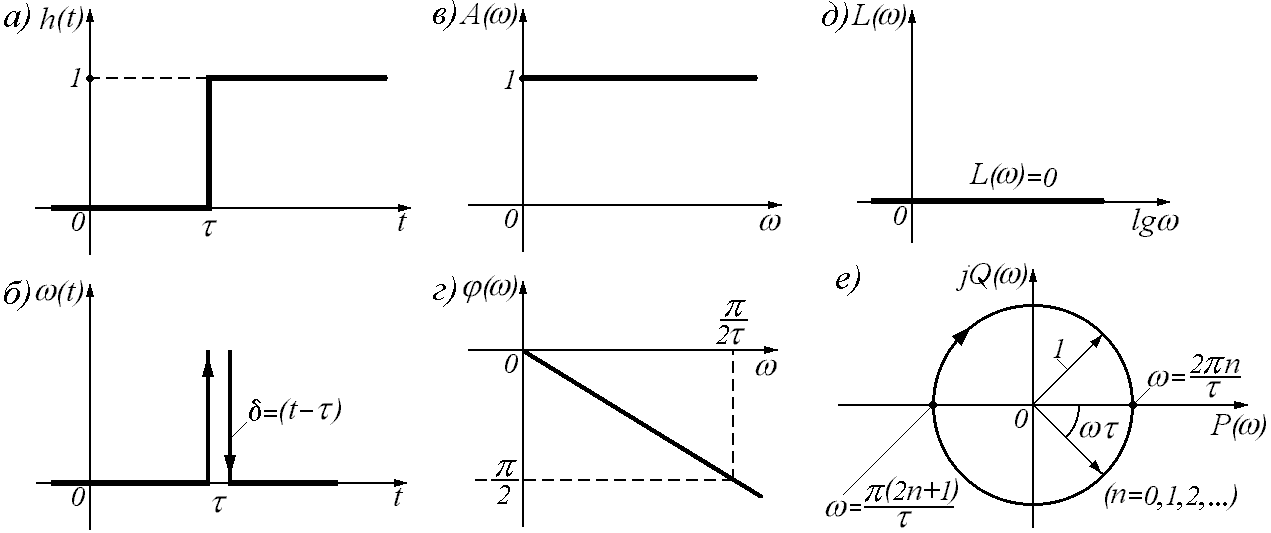
![]()
С
![]()
Звенья запаздывания в большинстве случаев ухудшают устойчивость систем и делают их трудноуправляемыми.
Если
ЗЗ входит в контур системы, то
характеристическое уравнение системы
будет уже не простым, а трансцендентным.
Решение и анализ трансцендентных
уравнений связаны с большими
трудностями![]() часто
в практических расчетах трансцендентную
передаточную функцию раскладывают в
ряд Пада и, учитывая только 2 или 3 члена
ряда, приближенно заменяют дробно-рациональной
функцией:
часто
в практических расчетах трансцендентную
передаточную функцию раскладывают в
ряд Пада и, учитывая только 2 или 3 члена
ряда, приближенно заменяют дробно-рациональной
функцией:
![]()
Другим
возможным способом аппроксимации ЗЗ
является его представление в виде
последовательного соединения nинерционных звеньев первого порядка с
постоянной времени![]()

Чем больше n, тем точнее аппроксимация.
