§ 71. Лінза. Формула тонкої лінзи. Збільшення лінзи

Головною частиною майже всіх оптичних приладів є лінзи — прозорі, скляні тіла, обмежені сферичними або циліндричними поверхнями. Типи лінз, їх оптичні харак­теристики, умовні позначення, принципи побудови зобра­жень у лінзах, способи визначення оптичної сили лінз

тощо ви вивчали у 8-му класі. В 11-му класі ви поглибите свої знання про лінзи, їх властивості і застосування.

Лінзи називають сферичними, якщо вони обмежені з двох чи з одного боку кульовими (сферичними) поверх­нями. Нижче термін «лінза» застосовуватиметься до сфе­ричних лінз, якщо немає примітки.

Як видно з малюнка 155, лінзи можна поділити на такі два типи.

1. Збирні (опуклі) лінзи (1, 2, 3), які мають більшу товщину поблизу центра, ніж біля країв.

2. Розсів ні (увігнуті) лінзи (4, 5, 6), які мають меншу товщину в центрі, ніж біля країв.

Однак це справедливо, лише коли показник заломлення речовини лінзи більший за показник заломлення навко­лишнього середовища. У протилежному випадку лінзи в більшою товщиною посередині будуть ровсівними, а з меншою — збирними.

Більшість лінз має дві поверхні, з яких одна або обидві сферичні чи циліндричні. Центр сфери або циліндра, час­тина яких становить поверхню лінзи, називають центром кривизни. У випадку, коли одна поверхня плоска, її також розглядають як частину сферичної поверхні з центром кривизни в нескінченності. Таким чином, кожна лінва має два центри кривизни С або С і два радіуси кривизни (мал. 156).

Пряма, яка проходить через центри кривизни С і С сферичних поверхонь лінзи, називається головною •птжч-ною віссю, вона перпендикулярна (нормальна) до повер­хонь лінзи у тих точках, через які проходить. Точку О, що лежить в лінзі на її оптичній осі і через яку промінь світла проходить, не змінюючи напряму, називають овтич-ннм центром лінзи. Будь-яка пряма, яка проходить через оптичний центр лінзи під кутом до головної оптичної осі, називається побічною оптичною віссю.

Точка F на головній оптичній осі збирної лінзи, в якій збираються промені, що падають на лінзу паралельно її головній оптичній осі, називається головним фокусом лінзи. Точка Fi на головній оптичній осі розсівної лінзи, в якій перетинаються продовження заломлених у лінзі розбіжних променів, що падають на неї паралельно голов­ній оптичній осі, називається уявним фокусом лінзи. У кожній лінзі є два фокуси, які лежать по обидва боки від неї.

Відстань від лінзи до фокуса називають фокусною від­станню лінзи. Умовилися фокусну відстань збирної лінзи вважати додатною, розсівної — від'ємною. Площини, які проходять через фокуси лінзи перпендикулярно до голов­ної оптичної осі, називають фокальними площинами.

Основна властивість лінз, яка використовується в оп­тичних приладах, полягає в тому, що всі промені, які виходять з однієї точки А перед лінзою, збираються в другій точці Лі за лінзою (мал. 157), або здається, що промені виходять з однієї точки А 2 перед лінзою (мал. 158).

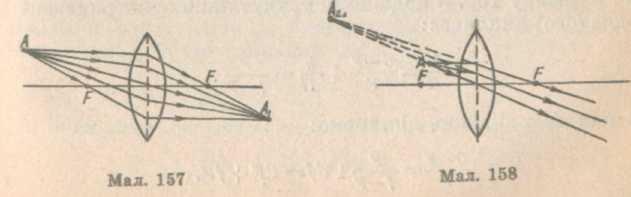
У першому випадку зображення точки А називають дійсним, у другому — уявним.

Чудовою властивістю світлових променів є їх оборот­ність: промінь, напрямлений протилежно до променя, який виходить з будь-якої оптичної системи, пройде через неї у зворотному напрямі точно тим самим шляхом, по якому пройшов у прямому напрямі перший промінь.

Зображення точки в лінзі графічно одержується як точка перетину всіх заломлених променів або їх про­довжень. У першому випадку зображення дійсне, в дру­гому — уявне. Як завжди, щоб знайти точку перетину всіх заломлених променів, досить побудувати будь-які два. Це можна зробити, скориставшись законом заломлення світла. Для цього треба виміряти кут падіння довільного

променя, за формулою закону заломленнязнайти

кут заломлення, побудувати заломлений промінь, який під певним кутом упаде на другу грань лінзи. Вимірявши цей кут падіння, треба за формулою знайти новий кут залом­лення і побудувати промінь, який виходить з лінзи. Це трудомістка робота, якої звичайно уникають. Пригадаємо з курсу фізики 8-го класу, що за відомими властивостями лінз можна побудувати три промені без всяких обчислень. Промінь, що падає паралельно будь-якій оптичній осі, після подвійного заломлення проходить через дійсний фокус або його продовження пройде через уявний фокус. За властивістю оборотності, промінь, який падає в напрямі на відповідний фокус, після подвійного заломлення вийде паралельно певній оптичній осі. Нарешті, через оптичний центр лінзи промінь пройде, не відхиляючись. Побудова зображення предмета в лінзі зводиться до побудови його крайніх точок.

Відстань / від збирної лінзи до зображення зв'язана з відстанню d від предмета до лінзи і фокусною відстанню F лінзи. Знайдемо цю залежність. Хід променів показано на малюнку 159. З подібності трикутників (заштриховані однаково) випливає:

З цих двох рівнянь дістанемо:

Поділивши обидві частини рівняння на добуток fdF_y ді­станемо:

(71.1)

Це рівняння називаєтьсяформулою лінзи. Вона засто­совується для знаходження відстані до зображення при будь-якому розташуванні предмета відносно лінзи.

Якщо значення відстані / буде від'ємним, це означає, що зображення предмета уявне і міститься по той самий бік від лінзи, що й предмет. Для розсівної лінзи значення фокусної відстані в розрахунках треба брати із знаком «мінус» і, оскільки зображення предмета дістаємо уяв­ним, відстань / до зображення завжди має бути зі знаком «мінус».

Пригадаємо з 8-го класу, що заломлююча здатність лінзи характеризується її оптичною силою — величиною, оберненою до фокусної відстані:

(71.2)

Виражається оптична силав діоптріях (дптр). Лінза з фокусною відстанню 1 м має оптичну силу в 1 дптр. Оптична сила збирної лінзи додатна, оптична сила роз­сівної лінзи від'ємна.

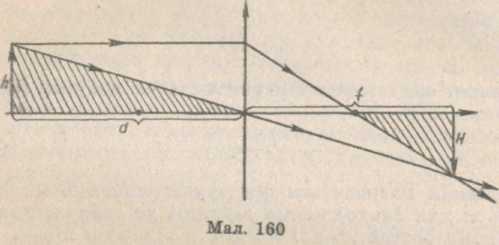
Залежно від положення предмета відносно лінзи ліній­ні розміри зображення змінюються. Відношення лінійних розмірів Я зображення до лінійних розмірів h предмета називається лінійним збільшенням Г:

(71.3) З подібності трикутників(мал. 160) випливає:

(71.4)

Із формул (71.1) і (71.4) або з побудови ходу променів видно, що для збирної лінзи при умовідійсне зобра-

ження буде зменшеним (Г< 1). При d=2F лінійні розмі­ри дійсного зображення дорівнюють розмірам предмета (^= !)• У випадкузображення дійсне, збіль-

шене (Г> 1). Якщо помістити предмет між фокусом і цент­ром лінзи, зображення буде збільшене, уявне.

Внвлва Ф