Лекции по математике. Теория вероятности

Неравенство Чебышева

Неравенство Чебышева, используемое для доказательства дальнейших теорем, справедливо как для непрерывных, так и для дискретных случайных величин.

Чебышѐв Пафнутий Львович - русский математик и механик.

Докажем неравенство Чебышева для дискретных случайных величин.

Теорема (первое неравенство Чебышеванеравенство

Маркова)

Для каждой неотрицательной случайной величины , имеющей математическое ожидание M [ ] , при любом 0 справедливо

P{ } М [ ] .

Пример Пусть - время опоздания студентов на лекцию. Известно, что M [ ] =1 мин. Оценить вероятность того,

что студент опоздает не менее чем на 5 минут.

Решение

Используя первое неравенство Чебышева

P{ } М [ ]

Имеем P{ 5} 15 .

151

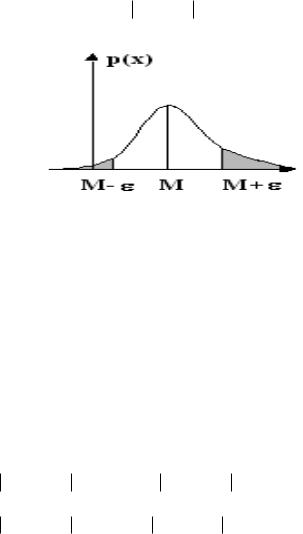
Теорема (второе неравенство Чебышева )

Для каждой СВ , имеющей дисперсию D[ ] 2 ,

при любом 0 справедливо

P{ M [ ] } 22

Неравенства Чебышева имеют не столь большое практическое значение, но огромное теоретическое для доказательства теорем из закона больших чисел.

противоположны, то:

p X M X ε p X M X ε 1,

следовательно,

p X M X ε 1 p X M X ε.

152

Найдем p X M X ε.

D X x1 M X 2 p1 x2 M X 2 p2 xn M X 2 pn

Исключим из этой суммы те слагаемые, для которых X M X ε. При этом сумма может только уменьшиться,

так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых.

Тогда

D X xk 1 M X 2 pk 1 xk 2 M X 2 pk 2

что и требовалось доказать.

Пример Средний расход воды на ферме составляет 1000 л в день, а среднее квадратичное =200 л. Оценить вероятность того, что расход воды в любой выбранный день не превысит 2000 л.

Решение

Т.к. границы интервала 0 2000 симметричны относительно M [ ] 1000 и

P{ 2000} P{0 2000} P{ 1000 1000},

153

Теоремы Чебышева и Бернулли

Обычно при измерении некоторой физической величины ее измеряют несколько раз и берут среднее арифметическое.

При каких условиях это правильно (частный случай теоремы Чебышева):

1)измерения попарно независимы;

2)имеют одно и тоже математическое ожидание;

3)дисперсии их ограничены.

Теорема Чебышева Если X 1 , X 2 , , X n – попарно

154

случайные величины с равномерно ограниченными дисперсиями, имеющие одинаковое математическое ожидание, равное а, то для любого сколь угодно малого ε 0 вероятность неравенства

X 1 X 2 X n a ε n

будет как угодно близка к 1, если число случайных величин достаточно велико. Иначе говоря,

Вывод: среднее арифметическое достаточно большого числа случайных величин принимает значения, близкие к сумме их математических ожиданий, то есть утрачивает характер случайной величины. Например, если проводится серия измерений какой-либо физической величины, причем:

а) результат каждого измерения не зависит от результатов остальных, то есть все результаты представляют собой попарно независимые случайные величины;

156

б) измерения производятся без систематических ошибок (их математические ожидания равны между собой и равны истинному значению a измеряемой величины);

в) обеспечена определенная точность измерений, следовательно, дисперсии рассматриваемых случайных величин равномерно ограничены; то при достаточно большом числе измерений их среднее арифметическое окажется сколь угодно близким к истинному значению измеряемой величины.

Практическое значение теоремы Чебышева

Если все измерения проводятся с одинаковой точностью2 , то дисперсия их средней

достаточно большом числе испытаний вероятность того, что модуль отклонения относительной частоты появлений A в n опытах от p будет сколь угодно малым, как угодно близка к 1:

157

Кроме того, рассматриваемые случайные величины попарно независимы и их дисперсии равномерно ограничены (так как

lim m p

n n

Речь идет лишь о вероятности того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой.

Разница заключается в следующем: при обычной сходимости, рассматриваемой в математическом анализе, для

всех n , начиная с некоторого значения, неравенство mn p ε

выполняется всегда; в нашем случае могут найтись такие значения n , при которых это неравенство неверно.

Этот вид сходимости называют сходимостью по вероятности.

Замечание Теорема Бернулли – следствие теоремы

m

Чебышева, т.к. статистическую вероятность события n

158

можно представить как среднее арифметическое n независимых случайных величин , имеющих одинаковый закон

распределения: 1n .

Предельные теоремы

Закон больших чисел не исследует вид предельного закона распределения суммы случайных величин. Этот вопрос рассмотрен в группе теорем, называемых центральной предельной теоремой. Они утверждают, что закон распределения суммы случайных величин, каждая из которых может иметь различные распределения, приближается к нормальному при достаточно большом числе слагаемых. Этим объясняется важность нормального закона для практических приложений.

Характеристические функции

Для доказательства центральной предельной теоремы используется метод характеристических функций.

Дадим определение характеристической функции.

 Определение Характеристической функцией случайной величины X называется функция

g t M eitX

Таким образом, g t представляет собой математическое ожидание некоторой комплексной случайной величины

UeitX , связанной с величиной X .

Вчастности, если X – дискретная случайная величина, заданная рядом распределения, то

itx

g t e k pk

k 1

159

Для непрерывной случайной величины с плотностью распределения f (x)

g t eitx f x dx

Пример Найдем характеристическую функцию для случайной величины X – число выпадений 6 очков при одном броске игральной кости.

Решение

Пример

Найдем характеристическую функцию для нормированной непрерывной случайной величины, распределенной по закону

160