Лекции по математике. Теория вероятности

Диаграммы Эйлера-Венна

Основные действия над событиями можно интерпретировать с помощью диаграмм Венна.

Леонард Эйлер (1707-1783) — российский и швейцарский математик, внѐсший значительный вклад в развитие теории вероятностей и ряда прикладных наук. Эйлер — автор более чем 800 работ. Почти полжизни провѐл в России, где внѐс существенный вклад в становление российской науки.

Диаграммы ВеннаЭйлера используется в математике, логике, менеджменте и других прикладных направлениях, обычно изображается в виде кругов одинакового радиуса.

Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют диаграммы Эйлера — Венна. На диаграмме ЭйлераВенна сумму событий можно изобразить в виде кругов (прямоугольник – изображение множества всех возможных исходов опыта). Диаграммы Венна нашли применение в современной логико-математической теории «формальных нейронных сетей».

Диаграмма, иллюстрирующая сумму совместных событий.

Диаграмма, иллюстрирующая сумму несовместных событий

41

Принцип практической невозможности

При решении многих практических задач приходится иметь дело с событиями, вероятность которых весьма мала, т. е. близка к нулю.

Можно ли считать, что маловероятное событие A в единичном испытании не произойдет? Такого заключения сделать нельзя, так как не исключено, хотя и мало вероятно, что событие A наступит.

Казалось бы, появление или не появление маловероятного события в единичном испытании предсказать невозможно. Однако длительный опыт показывает, что маловероятное событие в единичном испытании в подавляющем большинстве случаев не наступает.

На основании этого факта принимают следующий «принцип практической невозможности маловероятных событий»:

если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это событие не наступит.

Естественно возникает вопрос: насколько малой должна быть вероятность события, чтобы можно было считать невозможным его появление в одном испытании?

На этот вопрос нельзя ответить однозначно. Для задач, различных по существу, ответы будут разными.

Например, если вероятность того, что парашют при прыжке не раскроется, равна 0,01, то было бы недопустимым применять такие парашюты. Если же вероятность того, что поезд дальнего следования прибудет с опозданием, равна 0,01, то можно практически быть уверенным, что поезд прибудет вовремя.

 Определение Достаточно малую вероятность, при которой событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заключенные между 0,01 и 0,05.

Уровень значимости, равный 0,01, называют однопроцентным; уровень значимости, равный 0,02, называют

двухпроцентным и т. д.

43

Подчеркнем, что рассмотренный здесь принцип позволяет делать предсказания не только о событиях, имеющих малую вероятность, но и о событиях, вероятность которых близка к единице.

Действительно, если событие A имеет вероятность близкую к нулю, то вероятность противоположного события близка к единице. С другой стороны, не появление события A означает наступление противоположного события A .

Таким образом, из принципа невозможности маловероятных событии вытекает следующее важное для приложении следствие: если случайное событие имеет вероятность очень близкую к единице, то практически можно считать, что в единичном испытании это событие наступит.

Разумеется, и здесь ответ на вопрос о том, какую вероятность считать близкой к единице, зависит от существа задачи.

Контрольные вопросы

1.Что относится к основным понятиям теории вероятностей?

2.Назовите действия над событиями.

3.Виды случайных событий.

4.Дайте классическое определение вероятности.

5.Дайте статистическое определение вероятности.

6.Чему равна вероятность суммы двух несовместных событий?

7.Дайте определение произведения двух событий

8.Как определяется вероятность появления хотя бы одного события

9.Как определяется условная вероятность?

10.Сформулируйте теорему совместного появления двух событий.

11.Приведите формулу для вычисления вероятностей совместных событий.

44

Следствием двух основных теорем теории вероятностей – теоремы сложения и умножения – являются формула полной вероятности и формула Бейеса.

Формула Байеса, дает возможность оценить вероятность событий эмпирическим путѐм, играет важную роль в современной математической статистике и теории вероятностей.

Томас Байес (Бейес, Reverend Thomas Bayes]) (1702 —1761)

— английский математик. Математические интересы Байеса относились к теории вероятностей. Он сформулировал и решил одну из основных задач этого раздела математики (теорема Байеса). Работа, посвящѐнная этой задаче, была опубликована в 1763 году, уже после его смерти. Формула Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность того, что произошло какое-либо событие (гипотеза), имея на руках лишь косвенные тому подтверждения (данные), которые могут быть неточны. Названа в честь ее автора, преп. Томаса Байеса (посвященная ей работа впервые опубликована в 1763 году, уже после его смерти). Полученную по формуле вероятность можно далее уточнять, принимая во внимание данные новых наблюдений.

Изучение какого-либо объекта исследователь начинает с предположений ( версии, гипотезы).Например: экзаменатор, предлагающий студенту билет, выдвигает гипотезы, что студент учил материал и т.д.

 Определение Гипотезы Н1, Н2 , Нs - события, в

условиях которых только и может появиться событие A , обозначим Н1, Н2 , Нs

Вычисляя вероятность A выдвигаем различные предположения (гипотезы) относительно обстоятельств, которые могут привести к событию A .

 Определение Априорные гипотезы – гипотезы,

полученные до предстоящего опыта, апостериорные - после.

Формула Бейеса

45

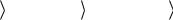
После выдвижения гипотезы исследователь ставит опыты, результат опыта фиксируют. На их основании надо высказать новое мнение о первоначальной гипотезе. Какая из них подтвердилась, какая нет. Стоит ли продолжать опыты? Как долго?

Томас Бейес изложил свой подход к решению таких задач. Томас Бейес (1702-1761) – английский математик, был священником.

Его формула позволяет эмпирически оценить вероятность события, работа была опубликована после его смерти. Она применяется, когда событие А , которое может появиться только

с одной из гипотез образующих полную группу

событий, произошло и необходимо произвести количественную переоценку априорных вероятностей этих гипотез, т.е. найти апостериорные условные вероятности .

46

Формула называется – формулой Бейеса Значение формулы Бейеса состоит в том, что при

наступлении события А , т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы.

Такой подход называемый бейесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе.

Замечание Формула Бейеса предназначена для вычисления апостериорных вероятностей гипотез после проведения опыта с учетом полученной информации (событие

Ауже произошло.

Замечание Психологические эксперименты показали, что люди при оценках вероятности игнорируют различие априорных вероятностей (ошибка базовой оценки), и потому правильные результаты, получаемые по теореме Бейеса, могут очень отличаться от ожидаемых.

Пример. После двух выстрелов двух стрелков, вероятности попаданий которых равны 0,6 и 0,7, в мишени оказалась одна пробоина. Найти вероятность того, что попал первый стрелок.

Решение

Пусть событие А – одно попадание при двух выстрелах, а гипотезы: H1 – первый попал, а второй промахнулся, H2 – первый промахнулся, а второй попал, H3 – оба попали, H4 – оба промахнулись. Вероятности гипотез:

47

Следовательно, полная вероятность

p A 0,18 1 0,28 1 0,42 0 0,12 0 0,46 .

Применяя формулу Бейеса, получим:

Пример Студент подготовил к экзамену 20 билетов из 25. В каком случае шансы взять известный билет больше - когда студент пришел на экзамен первым или вторым?

Решение

P 20 4 1 25 5

Найдем вероятность P2 взять известный билет, придя на экзамен

вторым, учитывая, что первый может взять как известный, так и неизвестный второму билет.

20 19 5 20 4

P2 25 24 25 24 5

Пример Студент приходит в медпункт и жалуется на плохое самочувствие. У медсестры две гипотезы H1 - он действительно болен, H2 - он здоров, но хочет получить справку. По внешнему виду она оценивает априорные

48

вероятности P H1 0,3 , P H2 0,7 и ставит ему градусник. Измеренная температура 37.5 (событие А ).

здоровых людей нормальная температура немного повышена или студент мог незаметно натереть градусник).

Теперь апостериорная вероятность того, что студент болен:

и у медсестры есть все основания направить студента к врачу.

Физический смысл и терминология формулы Бейеса

Формула Бейеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной.

События, отражающие действие «причин», в данном случае обычно называют гипотезами, так как они — предполагаемые

события, повлекшие данное.

Безусловную вероятность справедливости гипотезы называют априорной, а условную - с учетом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учетом данных о событии).

Можно также уточнять вероятность гипотезы, учитывая другие имеющиеся данные (другие произошедшие события). Для учета каждого следующего события нужно в качестве априорной вероятности гипотезы подставлять ее апостериорную вероятность с предыдущего шага.

Формулу Бейеса иногда называют формулой переоценки гипотез. Она позволяет дать оценку вероятности гипотез после

49

того, как произошло событие. Томас Бейес формулу не выводил, она названа в честь признания его работ по теории вероятностей.

Формула полной вероятности события

Важным следствием формулы Байеса является формула полной вероятности события, зависящего от нескольких несовместных гипотез (и только от них!).

Следствием двух основных теорем теории вероятностей – теоремы сложения и умножения – являются формула полной вероятности.

Теорема Полная вероятность события A равна сумме произведений вероятностей гипотез на условные вероятности события вычисленные соответственно при каждой из гипотез.

i s

P A P Hi P A Hi

i 1

Доказательство

Пусть А - событие, вероятность которого надо вычислить. Полагаем, что это события несовместимы, а их совокупность

охватывает всевозможные события, которые могут привести к

А, т.е. они образуют полную группу несовместимых событий. Вероятности их обозначим P H 1 , P H 2 , , P H s

На основании следствия из теоремы сложения

P H1 P H2 P Hs 1

Введем условные вероятности осуществления А при каждой из гипотез P A H1, P A H2 , , P A H s

Найдем полную вероятность события А

Событие А может наступить, если наступит событие H1 .

Вероятность наступления H1 и затем А на основании теоремы

умножения равна

P H1 и A P H1 P A H1

50