Лекции по математике. Теория вероятности

5. Верно ли, что математическое ожидание и среднее квадратическое отклонение показательно распределенной НСВ X совпадают.

7.Объясните почему распределение Гаусса называется нормальным?

8.Поясните на изменении кривой плотности распределения отказов влияние параметров распределения: математическое ожидания и дисперсии?

9.Почему нормальный закон распределения вынесен в отдельную тему теории вероятностей? К какому типу случайных величин он относится?

10.Что такое функция Лапласа, для чего она используется и какими свойствами обладает? Функция распределения нормально распределѐнной случайной величины.

11.Математическое ожидание и дисперсия нормально распределѐнной случайной величины, их влияние на график функции плотности вероятностей.

12.Свойства случайной величины, имеющей нормальный закон распределения. Правило трѐх сигм.

121

Задачи для самостоятельного решения

1.Математическое ожидание и стандартное отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (12, 14).

2.Математическое ожидание и стандартное отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (15, 25).

3.Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали больше 55 мм.

4.Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки

измерения Х подчинены нормальному закону со стандартным отклонением 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

5.Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная

величина Х распределена нормально со стандартным отклонением 0.4 мм. Найти, сколько в среднем будет годных шариков среди ста изготовленных.

6.Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 10 мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону со

122

ожиданием a 0 . Сколько процентов годных деталей изготавливает автомат?

7.Случайная величина Х распределена нормально с математическим ожиданием a 10 . Вероятность попадания Х в интервал (10, 20) равна 0,3. Чему равна вероятность попадания Х в интервал (0, 10)?

8.Случайная величина Х распределена нормально с

математическим ожиданием a 25 . Вероятность попадания Х в интервал (10, 15) равна 0,2. Чему равна вероятность попадания Х в интервал (35, 40)?

9. Случайная величина Х распределена нормально с математическим ожиданием a 10 и стандартным отклонением5 . Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 попадет величина Х в результате испытания.

10. Случайная величина Х распределена нормально со стандартным отклонением 5 мм. Найти длину интервала, симметричного относительно математического ожидания, в

123

значений X .

Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей Y yi .

Пример Дан закон распределения двумерной случайной величины:

Найти законы распределения составляющих.

Решение Складывая стоящие в таблице вероятности «по столбцам», получим ряд распределения для X :

125

Числовые характеристики двумерных случайных величин

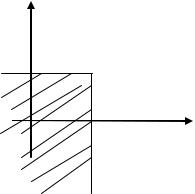
 Определение Функцией распределения F(x, y) двумерной случайной величины X ,Y называется вероятность того, что

X x , a Y y :

F x, y p X x, Y y .

1) 0 F x, y 1 (так как F x, y является вероятностью). 2) F x, y есть неубывающая функция по каждому

аргументу:

F x2 , y F x1, y ,если x2 x1 ; F x, y2 F x, y1 ,если y2 y1 .

Доказательство

F x2 y p X x2 ,Y y p X x1,Y y p x1 x x2 ,Y yp X x1,Y y F x1, y

Аналогично доказывается и второе утверждение.

126

невозможны ( так как невозможно событие x или y ),

то F x, p X x F1 x . Аналогично доказывается второе

утверждение.

 Определение Плотностью совместного распределения

вероятностей (двумерной плотностью вероятности) непрерывной двумерной случайной величины называется смешанная частная производная 2-го порядка от функции распределения:

представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами х и y к

площади этого прямоугольника при х 0, у 0.

127

Свойства двумерной плотности вероятности

1)f x, y 0

(вероятность попадания точки в прямоугольник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).

yx

2)F (x, y) f (x, y)dxdy

Найдем вероятность того, что точка, координаты которой

принадлежащей прямоугольнику.

Тогда вероятность попадания точки в область D есть предел

n

интегральной суммы f ( i , i ) x y , то есть

i 1

p(( X ,Y ) D) f (x, y)dxdy.

D

 Определение Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.

128

Определение Сумма случайных величин Х и Y -

случайная величина X Y , возможные значения которой равны суммам каждого возможного значения X с каждым возможным значением Y ; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго).

Определение Произведение независимых случайных величин Х и Y - случайная величина XY, возможные значения которой равны произведениям всех возможных значений X на все возможные значенияY , а соответствующие им вероятности равны произведениям вероятностей сомножителей.

Математическое ожидание двумерных случайных величин

 Теорема Математическое ожидание суммы двух случайных величин ( зависимых или независимых ) равно сумме

математических ожиданий слагаемых:

M X Y M X M Y .

Доказательство

Рассмотрим случайные величины, заданные рядами распределения, тогда возможными значениями X Y являются x1 y1 , x1 y2 , x2 y1 , x2 y2 .

примет значения x1 y1 или x1 y2 и вероятность которого равна p11 p22 , совпадает с событием, заключающемся в том, что X x1 (его вероятность – р1).

Аналогично доказывается, что

p21 p22 p2 , p11 p21 g1 , p12 p22 g2 .

M X Y x1 p1 x2 p2 y1 g2 M X M Y .

129

 Замечание сумма любого числа случайных величин равна сумме математических ожиданий слагаемых.

Пример Найти математическое ожидание суммы числа очков, выпавших при броске пяти игральных костей.

Решение

Найдем математическое ожидание числа очков, выпавших при броске одной кости:

M X1 = (1 + 2 + 3 + 4 + 5 + 6) 16 72 .

Тому же числу равно математическое ожидание числа очков, выпавших на любой кости. Следовательно, по свойству 4

M X = 5 16 56 .

 Теорема Математическое ожидание произведения двух независимых случайных величин равно произведению их

математических ожиданий:

M XY M X M Y .

Доказательство

Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:

Следовательно,

130