
Лекции по математике. Теория вероятности
.pdf
Здесь x , |
y - варианты (наблюдавшиеся значения) признаков X |
|||||||||||||||
и Y , |
nxy |
- частота пары вариант x, |
y , n |
- объем выборки, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x , y |
- выборочные средние. |
Найдем выборочные средние с |
|||||||||||||
помощью соотношения: |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
nx x |
, |
|
|
1 |
ny y , |
|
|
|
|
|
|
|
|
x |
y |
||||||||
|
|
|
|
|
|
|
|
n |
||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||
где |
nx , n y - |
частоты |
вариант |
x |
и y . Так как |
|||||||||||
n 20 10 30 10 20 10 100, получаем
1(20 0) 0 10 10 1 0 20 2 30 10
x 0,8 100
y 2 20 10 0 30 3 0 10 20 10 2,4 . 100
Тогда
xy 2 1 20 2 0 10 2 1 0 2 2 30 3 1 0 3 0 10 3 1 20 3 2 10 100
0,8 2,4 0,8.
Контрольные вопросы
1.Что такое ковариация?
2.Приведите примеры «положительной корреляции»
3.К каким изменениям коэффициента корреляции приводят ошибки измерений тех признаков для которых оценивается взаимосвязь.
4.Может ли коэффициент корреляции быть равным нулю , если между измеряемыми признаками существует функциональная зависимость?
5.Приведите пример случайных величин, у которых ковариация нулевая.
6.Какие характеристики составляют корреляционную матрицу?
141

Лекция 9
Функция одного случайного аргумента
При решении задач часто удобно бывает представить исследуемую случайную величину как функцию других случайных величин с известными законами распределения, что помогает установить и закон распределения заданной случайной величины.
|
Определение |
Если |
каждому возможному |
значению |
|||||||
случайной величины X соответствует одно возможное значение |
|||||||||||
случайной величины Y , то случайную величину Y |
называют |
||||||||||
функцией случайного аргумента X : |
|
|
|
||||||||
|
|
|
|
|
|
|
Y (X) . |
|
|||
Выясним, как найти закон распределения функции по |
|||||||||||
известному закону распределения аргумента. |
|
||||||||||
1) Пусть аргумент |
X |
– дискретная случайная величина, |
|||||||||
причем |
|
различным |
значениям X |
соответствуют |
различные |
||||||
значения Y . |
|
|
|
|
|
|
|
|
|||
Тогда вероятности |
соответствующих значений |
X и Y |
|||||||||
равны.. |
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Ряд распределения для X имеет вид: |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
p |
|
0,1 |
|
0,2 |
|
|
0,3 |
|
0,4 |
|
|
Найдем закон распределения функции Y 2 X 2 3 : |
|||||||||||
Решение |
|
|
|
|
|
|
|
|
|||
Закон распределения функции будет иметь вид: |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
47 |
|
69 |
|
|
95 |
|
125 |
|
|
p |
|
0,1 |
|
0,2 |
|
|
0,3 |
|
0,4 |
|
|
(при вычислении значений Y в формулу, задающую функцию, подставляются возможные значения X ).
2) Если разным значениям X могут соответствовать одинаковые значения Y , то вероятности значений аргумента,
142

при которых функция принимает одно и то же значение, складываются.
|
Пример Ряд распределения для X имеет вид: |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
0 |
|
|
1 |
|
2 |
|
3 |
|
|
|
p |
|
0,1 |
|
0,2 |
0,3 |
0,4 |
|
|
|
|||
Найдем закон распределения функции Y X 2 |
2 X : |
|||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|||
Закон распределения функции |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
-1 |
|
0 |
|
3 |
|
|
|
|
|
|
p |
|
0,2 |
|
0,4 |
|
0,4 |
|
|
|
|
(так |
|
как |
|
Y 0 |
при |
X 0 |
и |
X 2 , то |
||||
p(Y 0 ) p(X |
0 ) p(X 2 ) 0,1 0,3 0,4 ). |
|||||||||||
Математическое ожидание функции одного аргумента
Пусть Y (X)– функция случайного аргумента X , и требуется найти ее математическое ожидание, зная закон
распределения X . |
|
|
|
||||
1) |
Если X – дискретная случайная величина, то |
||||||
|
|
|
|
|
|
n |
|
|
|
|
M (Y ) M ( (x)) (xi ) pi . |
||||
|
|
|
|
|
|
i 1 |
|
|
Пример Найдем M(Y) , если случайная величина Y |
||||||
задана рядом распределения: |
|
|
|
||||
|
|
|
|
|
|
|
|
Y |
|
47 |
69 |
|
95 |
125 |
|
p |
|
0,1 |
0,2 |
|
0,3 |
0,4 |
|
Решение
M(Y) 47 0,1 69 0,2 95 0,3 125 0,4 97
143
Если X – непрерывная случайная величина, то математическое ожидание функции одного аргумента можно искать по-разному.
Если известна плотность распределения g(y) , то
M (Y ) yg( y)dy.
Если же g(y) найти сложно, то можно использовать известную плотность распределения f(x) :
M (Y ) (x) f (x)dx.
Вчастности, если все значения X принадлежат
промежутку (a, b) , то
b
M (Y ) (x) f (x)dx.
а
Функция двух случайных величин
Определение Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z , то Z называют функцией двух случайных аргументов X и Y :
Z ( X,Y ) .
Рассмотрим в качестве такой функции сумму X Y . В некоторых случаях можно найти ее закон распределения, зная законы распределения слагаемых.
1) Если |
X |
и |
Y |
– дискретные |
независимые случайные |
|
величины, |
то |
для |
определения |
закона |
распределения |
|
Z X Y |
нужно |
найти все возможные |
значения Z и |
|||
соответствующие им вероятности.
 Пример Рассмотрим дискретные случайные величины X и Y , законы распределения которых имеют вид:
Пример Рассмотрим дискретные случайные величины X и Y , законы распределения которых имеют вид:
144

|
|
|
X |
|
|
|
-2 |
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
p |
|
|
|
0,3 |
|
0,4 |
|
0,3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Y |
0 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
p |
0 |
|
0 |
0,3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
,2 |
|
,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем возможные значения Z : |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
-2 0 -2 ( p 0,3 0,2 0,06 ), |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
-2 1 -1 (p 0,3 0,5 0,15 ), |
|
|
|
||||||||||||
|
|
|
|
|
|
|
-2 2 0 (p 0,3 0,3 0,09 ), |
|
|
|
||||||||||||
|
|
|
|
|
1 0 1 (p 0,4 0,2 0,08 ), |
|
|
|
||||||||||||||
|
|
|
|
|
1 1 2 (p 0,4 0,5 0,2 ), |
|
|
|
||||||||||||||
|
|
|
|
|
1 2 3 (p 0,4 0,3 0,12 ), |
|
|
|
||||||||||||||
|
|
|
|
|
3 0 3 (p 0,3 0,2 0,06 ), |
|
|
|
||||||||||||||
|
|
|
|
|
3 1 4 (p 0,3 0,5 0,15 ), |
|
|
|
||||||||||||||
|
|
|
|
|
3 2 5 (p 0,3 0,3 0,09 ) |
|
|
|
||||||||||||||
|
|
Сложив |
вероятности |
повторившегося дважды |
значения |
|||||||||||||||||
|
Z 3, составим ряд распределения для Z : |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
-2 |
|
|
|
-1 |
|
|
0 |
|
1 |
|
|
2 |
|
3 |
|
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
p |
|
0,06 |
|
0,15 |
|
|
0,09 |
|
0,08 |
|
|
0,2 |
|
0,18 |
|
0,15 |
|
0,09 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2) |
Если |
X и |
|
Y – непрерывные независимые случайные |
||||||||||||||||
величины, то, если плотность вероятности хотя бы одного из аргументов задана на (- , ) одной формулой, то плотность
суммы g(z) можно найти по формулам
145
|
|
g(z) |
f1 (x) f2 (z x)dx f1 (z y) f2 ( y)dy, |
|
|
где f1 (x) , f2 ( y) |
– плотности распределения слагаемых. Если |
возможные значения аргументов неотрицательны, то |
|
z |
z |
g(z) |
f1 (x) f2 (z x)dx f1 (z y) f2 ( y)dy. |
0 |
0 |
Замечание Плотность распределения суммы двух независимых случайных величин называют композицией.
146
Лекция 10
Равномерный закон распределения на плоскости
Определение Система двух случайных величин называется равномерно распределенной на плоскости, если ее
плотность вероятности
f x, y = const
внутри некоторой области и равна 0 вне ее. |
|
||||
Пусть |
данная |
область |
– |
прямоугольник |
вида |
a x b, c y d.
Тогда из свойств функции плотности f x, y следует, что
|
1 |
|
|
1 |
|
|
внутри прямоугольника, |
||||
f (x, y) |
|
|
(b a)(d c) |
|
|||||||
|
|
|
|
||||||||
Snp |
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
вне его. |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
Найдем двумерную функцию распределения: |
|||||||||||
|
|
|
1 |
|
y |
x |
|
(x a)( y c) |
|
||
F (x, y) |
|
|
|
dxdy |
|
||||||
(b a)(d c) |
|
(b a)(d c) |
|||||||||
|
c |
a |
|
||||||||
|
|
|
|
|
|
|
|
||||
при a x b,c y d ,
F x, y 0 при x a, y c ,
F x.y 1при x b, y d .
Функции распределения составляющих, имеют вид:
F (x) |
x a |
, |
F ( y) |
y c |
. |
|
|
||||
1 |
b a |
|
2 |
d c |
|
|
|
|
|||
147

Нормальный закон распределения на плоскости
Из законов распределения системы двух случайных величин имеет смысл специально рассмотреть нормальный закон, как имеющий наибольшее распространение на практике. Так как система двух случайных величин изображается случайной точкой на плоскости, нормальный закон для системы двух величин часто называют «нормальным законом на плоскости». Многочисленные исследования, проведѐнные профессорами А.Б.Яхиным, А.А.Зыковым и другими, показали, что распределение действительных размеров деталей изготовленных, обработанных на настроенных станках, очень часто подчиняется закону нормального распределения (закону Гаусса).
Это объясняется тем, что результирующая погрешность обработки обычно формируется в результате одновременного воздействия большого числа погрешностей, зависящих от станка, приспособления, инструмента и заготовки, которые по существу представляют собой взаимно независимые случайные величины. Влияние каждой из них на результирующую погрешность имеет один порядок, поэтому распределение результирующей погрешности обработки, а значит, и распределение действительных размеров изготовленных деталей подчиняются закону нормального распределения
Определение Нормальный закон распределения на плоскости - распределение вероятностей двумерной случайной величины (X, Y), если плотность распределения
|
|
|
|
|
|
1 |
|
|
x a1 2 |
y a2 2 |
x a1 |
|
y a2 |
|
|
|
|
|
|
|
|
|
|
2 |
2 2 xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
2 |
|
|
x |
|
y |
|
|||
f x, y |
|
|
|
e |
2 1 xy |
|
x |
y |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
2 |
y |
1 r 2 |
|
|
|
|
|
|
|
|
|
||
|
x |
xy |
|
|
|
|
|
|
|
|
|
|||
Нормальный закон на плоскости определяется 5 параметрами: a1, a2 – математические ожидания,
x , y – средние квадратические отклонения, rxy – коэффициент корреляции Х и Y.
Ниже показан график плотности нормального распределения
148
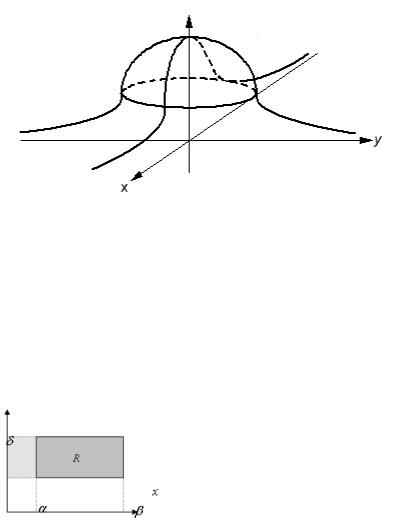
Вероятность попадания в прямоугольник |
|
|
|
|
|
||||||||||||||||||||
Пусть случайная точка на плоскости подчинена |
|
||||||||||||||||||||||||
нормальному закону |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ay 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x ax |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
f x, y |
|
|
|
|
x2 |
|
y2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вероятность |
|
попадания |
|
случайной |
|
точки |
X ,Y |
в |
|
||||||||||||||||
прямоугольник стороны которого |
|
параллельны координатным |
|
||||||||||||||||||||||
|
|
|
|
|
|
осям |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P X ,Y R f x, y dxdy |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P X ,Y R |
|
|
a |
x |
|
|
|
a |
x |
|
|
|
|
ay |
|
|
ay |
||||||||
Φ |
|
|
Φ |
|
|
|
|
|
|
|
Φ |
|
|
|
|
Φ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
x |
|
|
0 |
|
|
x |
|
|
|
0 |
|
y |
|
0 |
|
y |
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Φ0 x - нормальная функция распределения.
149
Лекция 11
Закон больших чисел
Изучение статистических закономерностей позволило установить, что при некоторых условиях суммарное поведение большого количества случайных величин почти утрачивает случайный характер и становится закономерным (иначе говоря, случайные отклонения от некоторого среднего поведения взаимно погашаются). В частности, если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному.
Математическая формулировка этого утверждения дается в группе теорем, которые принято называть законами больших чисел.
Сущность закона больших чисел состоит в том, что при большом числе независимых опытов частота появления какогото события близка к его вероятности.
Пример
|
|
P 100 |
Если из большого |
||||
|
|
мешка |
с |
орехами |
|||
|
|
|
|||||
|
|
|
достать |
любые |
10 |
||
|
|
|
штук и 5 из них |
||||
|
|
|
будут |
|
пустыми, |
||
|
|
|
можно |
|
делать |
||
|
|
|
выводы |
|
|
о |
|
45 |
50 |
55 |
содержимом всего |
||||
мешка. |
Вывод |
в |
|||||
|
|
|
|||||
количество полных орехов |
мешке |
|
―почти |
||||
|
|
|
половина‖ |
всех |
|||
орехов пустые имеет для этого определенное основание.
Имеется вероятность в две трети за то, что в мешке находится не меньше 45 процентов и не больше 55 процентов полных орехов.
150
