Лекции по математике. Теория вероятности

Лекция 13

Проверка статистических гипотез

Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид (назовем его A ), выдвигают гипотезу: генеральная совокупность распределена по закону A . Таким образом, в этой гипотезе речь идет о виде предполагаемого распределения.

Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предположить, что неизвестный параметр равен определенному значению 0 ,

выдвигают гипотезу: 0 . Таким образом, в этой гипотезе

речь идет о предполагаемой величине параметра одного известного распределения.

Возможны и другие гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок и многие другие.

 Определение Статистическая гипотеза – гипотеза о виде неизвестного распределения, или о параметрах известных распределений.

Например, статистическими будут гипотезы:

1)генеральная совокупность распределена по закону Пуассона;

2)дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, во второй - о параметрах двух известных распределений.

Гипотеза «в 2010г. не будет дождей» не является статистической, поскольку в ней не идет речь ни о виде, ни о параметрах распределения.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза.

192

По этой причине эти гипотезы целесообразно различать. Нулевой (основной) называют выдвинутую гипотезу H0 .

Конкурирующей (альтернативной) называют гипотезу H1 ,

которая противоречит нулевой.

Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может

Нулевая гипотеза представляет собой такое утверждение, которое принимается тогда, когда нет убедительных аргументов для его отклонения.

Альтернативную гипотезу принимают только тогда, когда есть убедительное статистическое доказательство, которое отвергает нулевую гипотезу.

Определяя, какая из двух гипотез будет альтернативной,

распределения, то гипотеза H 0 : 5 простая.

Пример Гипотеза H 0 : математическое ожидание

нормального распределения равно 3 ( известно) - простая. Сложной называют гипотезу, которая состоит из конечного

bi любое число, большее 5.

Гипотеза H 0 : математическое ожидание нормального распределения равно 3 ( неизвестно) - сложная.

193

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно.

Эту величину обозначают через U или Z, если она распределена нормально, F или v2 - по закону Фишера -

Снедекора, Т - по закону Стьюдента, 2 - по закону «хи квадрат» и т. д.

Признаем, что и принимая, и отвергая H0 , мы подвергаем

себя определѐнному риску.

В итоге статистической проверки могут быть допущены ошибки двух типов:

1.Ошибка 1 рода - будет отвергнута правильная гипотеза. Принимается H1 , тогда как верна H0 .

2.Ошибка 2 рода – будет принята неправильная гипотеза. Примем H0 , тогда как на самом деле верна H1 .

Пример H0 - подсудимый невиновен ( гипотеза либо

принимается, либо отвергается). Могут быть 2 ошибки: 1.осудить невиновного (1 рода)

2.оправдать виновного (2 рода) Последствия ошибок разны.

Пример Идет строительство дома. Однако выявлены ряд ошибок в проекте и самом строительстве. Продолжать ли стройку? H0 - продолжать.

Ошибка 1 рода – остановили стройку. Денежные потери. Ошибка 2 рода – продолжили строительство. Дом обвалился. Вероятность совершить ошибку 1 рода (отвергнуть

правильную H0 ) обычно обозначается и называется уровнем значимости.

194

Если 0.05 , то это означает, что имеется риск в 5 случаях

отличается от интервального оценивания, где рассматривалась только одна ошибка.

 Определение Статистический критерий (или просто

критерий)- случайная величина K , которая служит для проверки нулевой гипотезы.

Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия K принимают отношение исправленных выборочных дисперсий:

Эта величина случайная, потому что в различных опытах дисперсии будут принимать различные, наперед неизвестные значения.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин, и таким образом получают частное (наблюдаемое) значение критерия.

Наблюдаемым значением назначают значение

критерия, вычисленное по выборкам.

Например, если по двум выборкам, извлеченным из

195

Общий алгоритм

1.Сформулировать нулевую и альтернативную гипотезы.

2.Задать уровень значимости (допустимую вероятность ошибки 1 рода).

3.Выбрать подходящий критерий (меру расхождения) K

4.Определить критическую область.

5.По выборочным данным найти фактическое значение критерия..

6.Если наблюденное значение критерия принадлежит критической области, то нулевая гипотеза отклоняется, иначе – принимается.

Если H0 принята, она ещѐ не доказана. Говорят, что данные согласуются с H0

Если гипотеза отвергается, то этот вывод более категоричен. Пример Для проведения экзамена по курсу «Теория вероятностей» подготовлено 100 вопросов. Если студент знает не менее 60 вопросов, считается, что он усвоил курс и ему может быть поставлен экзамен. Каждому студенту предлагается 5 вопросов. Студент получает экзамен, если ответит не менее, чем на 3 вопроса.

Решение

Генеральная совокупность – 100 вопросов. Выборка –5 вопросов. Гипотеза H0 - «студент курса не усвоил». Критерием

для проверки служит число правильных ответов. Областью принятия гипотезы является совокупность чисел 0,1,2, а критической областью – 3,4,5.

Пусть «хороший» студент знает 70 из 100 вопросов и объективно должен получить экзамен. Тогда H0 неверна. Но

возможно, что из 5 вопросов студент будет знать меньше 3 и не получит экзамен. Произойдет ошибка 2 рода.

Наоборот, «плохой» студент, знающий 30 вопросов, может получить 3 и более известных вопросов. В этом случае будет отвергнута правильная гипотеза H0 и произойдет ошибка

1 рода.

196

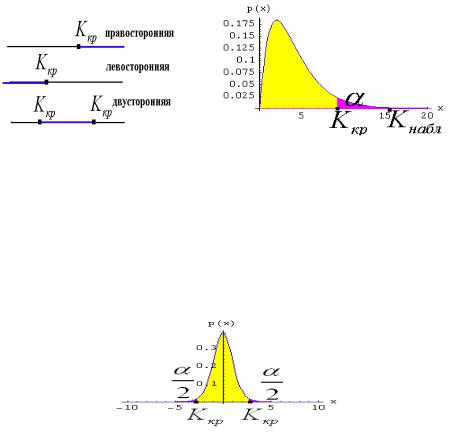
Как уменьшить вероятность ошибок 1 и 2 рода? Можно уменьшить вероятность ошибки 1 рода путем сужения критической области (ставить экзамен за 4 или 5 правильных ответов). Но при этом возрастет и вероятность ошибки 2 рода. Одновременное уменьшение вероятностей ошибок 1 и 2 рода возможно только за счет увеличения объема выборки, т.е. числа предлагаемых вопросов.

Критическая область

Как построить критическую область.

1.Задаем уровень значимости .

2.Зная закон распределения K ищем Kкр , исходя из

требования (для односторонней области)

K > Kкр или K Kкр .

отвергаем H0 .. В противном случае принимаем H0 с уровнем значимости .

197

Если критерий двусторонний, то критические точки

Распределение 2

Пусть X i i 1,2, , n — независимые случайные

величины, распределенные по гауссовскому закону, причем м.о. каждой из них равно нулю, а с.к.о. — единице.

Тогда сумма квадратов этих величин распределена по закону2 (''хи квадрат") с k n степенями свободы.

2 Xi2 i 1n

Плотность этого распределения

где Γ x = t x 1e t dt гамма-функция, в частности, Γ n 1 n!

Распределение 2 определяется одним параметром — числом степеней свободы k .

С увеличением числа k распределение медленно приближается к гауссовскому.

198

Критерий Пирсона

Одной из важнейших задач математической статистики является установление теоретического закона распределения случайной величины по эмпирическим данным.

Предположение о виде закона распределения может быть выдвинуто, исходя из теоретических предпосылок, опыта предшествующих исследований и на основании графического представления опытных данных. Параметры распределения заменяют их точечными оценками.

Между теоретическим и эмпирическим распределениями неизбежны расхождения. Возникает вопрос: объясняются ли эти расхождения случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что теоретический закон подобран неудачно. Для ответа на этот вопрос служат критерии согласия.

Определение Критерий согласия -критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Статистические критерии подразделяются на следующие категории:

Критерии значимости. Проверка на значимость предполагает проверку гипотезы о численных значениях

известного закона распределения: 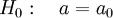— нулевая

гипотеза. или 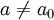— конкурирующая гипотеза.

Критерии согласия. Проверка на согласие подразумевает проверку предположения о том, что исследуемая случайная величина подчиняется предполагаемому закону. Критерии согласия можно также воспринимать, как критерии значимости.

Критерии на однородность. При проверке на однородность случайные величины исследуются на факт взаимного соответствия их законов распределения (подчиняются ли эти величины одному и тому же закону). Используются в факторном (дисперсионном) анализе для определения наличия зависимостей.

199

Это разделение условно, и зачастую один и тот же критерий может быть использован в разных качествах.

Критерий Пирсона, или критерий χ2 — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H0 о том, что эта случайная

величина подчиняется закону распределения F x . Для проверки гипотезы произведѐм выборку, состоящую из n независимых наблюдений над случайной величиной X . По

выборке можно построить эмпирическое распределение F x исследуемой случайной величины. Сравнение эмпирического

и теоретического распределений производится с помощью специально подобранной случайной величины — критерия согласия. Одним из таких критериев и является критерий Пирсона.

Пусть проведено n независимых опытов, в каждом из которых случайная величина приняла определенное значение. Все значения упорядочены в таблице

200