Лекции по математике. Теория вероятности

2) Если случайные величины X и Y связаны соотношением Y Ax , то их характеристические функции связаны

соотношением

gy t gx at .

3) Характеристическая функция суммы независимых случайных величин равна произведению характеристических

аналогично). Согласно условию теоремы, характеристические функции слагаемых одинаковы:

Найдѐм:

161

отличающуюся от Yn тем, что ее дисперсия при любом n равна

0.

Так как Yn и Zn связаны линейной зависимостью, достаточно доказать, что Zn распределена по нормальному закону, или, что

то же самое, что ее характеристическая функция приближается к характеристической функции нормального закона. По свойству характеристических функций

Прологарифмируем полученное выражение: ln gxn t n ln 1 k ,

162

характеристическая функция нормального распределения.

Итак, при неограниченном увеличении числа слагаемых характеристическая функция величины Zn неограниченно приближается к характеристической функции нормального закона; следовательно, закон распределения Zn ( и Yn )

неограниченно приближается к нормальному. Теорема доказана.

Ляпунов Александр Михайлович(1857-1918).Русский математик и механик. Исследовал проблемы устойчивости движения материальных систем. Методы, предложенные Ляпуновым, применяются во многих разделах теории дифференциальных уравнений. Дал простое и строгое доказательство центральной предельной теоремы в общем виде. Для доказательства разработал метод характеристических функций, который широко применяется в современной теории вероятностей.

 Замечание (практическое значение предельной теоремы) Пусть производится измерение некоторой физической величины. Каждое из измерений является приблизительным, на него влияют многие факторы – температура, колебания прибора, влажность и т.д. Каждый из факторов порождает ничтожно малую ошибку, но совокупность факторов – заметную

163

суммарную ошибку. Рассматривая суммарную ошибку как сумму очень большого числа взаимно независимых случайных величин, можно заключить, что ошибка имеет нормальное распределение. На этом строится статистическое оценивание погрешности.

А.М.Ляпунов доказал центральную предельную теорему для условий более общего вида:

Теорема (теорема Ляпунова) Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, для которых выполнено условие:

где bk – третий абсолютный центральный момент величины X k ,

аDk – ее дисперсия, то X имеет распределение, близкое к

нормальному ( условие Ляпунова означает, что влияние каждого слагаемого на сумму ничтожно мало).

Практически можно использовать центральную предельную теорему при достаточно небольшом количестве слагаемых, так как вероятностные расчеты требуют сравнительно малой точности.

Опыт показывает, что для суммы даже десяти и менее слагаемых закон их распределения можно заменить нормальным.

 Замечание Смысл условия теоремы состоит в том, чтобы в сумме не было слагаемых, влияние которых на разброс подавляюще велико по сравнению с остальными и не должно быть большого числа слагаемых, влияние которых очень мало. Т.о. удельный вес каждого отдельного слагаемого должен стремиться к нулю при увеличении числа слагаемых.

Частным случаем центральной предельной теоремы для дискретных случайных величин является теорема МуавраЛапласа.

164

Муавр Абрахам (1667-1754) - английский математик. Труды по теории рядов, теории вероятностей, теории комплексных чисел. В теории вероятностей доказал важную предельную теорему (1730). В теории комплексных чисел вывел правила возведения в степень и извлечения корней.

Лаплас Пьер Симон (1749-1827) -французский математик, физик и астроном. Фундаментальные работы по математике, экспериментальной и математической физике и небесной механике. Является одним из создателей теории вероятностей. Доказал важную предельную теорему, развил теорию ошибок. Ввел теоремы сложения и умножения вероятностей, понятия производящих функций и математического ожидания.

Теорема (теорема Муавра-Лапласа) Если производится n независимых опытов, в каждом из которых событие A появляется с вероятностью p , то справедливо соотношение:

распределенной по нормальному закону и нормированной, следовательно, вероятность ее попадания в интервал α,β

можно найти по формуле

p α Z β Φ β Φα.

Поскольку Y имеет биномиальное распределение, my np ,

Dy npq , y 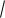npq .

165

Тогда Z Y np .

npq

Подставляя это выражение в предыдущую формулу, получим равенство

Следствие В условиях теоремы Муавра-Лапласа вероятность того, что событие A появится в n опытах ровно k раз, при большом количестве опытов можно найти по формуле:

приводятся в специальных таблицах).

Пример Найти вероятность того, что при 100 бросках монеты число выпадений герба окажется в пределах от 40 до 60.

Решение

Применим формулу

Пример

166

В условиях предыдущего примера найти вероятность того, что выпадет 45 гербов.

Решение

Найдем x 45 50 1, тогда

5

p100 15 1 15 1 15 0,2420 0,0484.

Контрольные вопросы

1.Что такое закон больших чисел в широком смысле и в узком смысле?

2.Что позволяет оценить неравенство Чебышева?

3.Сформулируйте теорему Чебышева и условия еѐ применения.

4.Сформулируйте теорему Бернулли и теорему Пуассона.

5.Что устанавливает центральная предельная теорема?

6.Сформулируйте теорему Ляпунова.

7.Сформулируйте условия, при которых нормальное распределение может служить аппроксимацией к биноминальному.

167

Лекция 12

Математическая статистика

Математическая статистика изучает различные методы сбора, обработки и осмысления результатов многократно повторяемых случайных событий. Понятие случайного события определяется в теории вероятностей, обработка результатов также производится при помощи теоретически разработанных вероятностных методов.

Для процесса построения и применения моделей характерно, чем больше данных, тем точнее, адекватнее модель. О современной математической статистике можно говорить как о науке о принятии решений в условиях неопределенности.

 Определение Математическая статистика – раздел математики, занимающейся установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений.

Двумя основными задачами математической статистики являются:

- определение способов сбора и группировки этих статистических данных;

- разработка методов анализа полученных данных в

зависимости от целей исследования, к которым относятся:

а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.;

б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения.

Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов.

168

Пример Имеется партия деталей, качественным признаком может служить стандартность детали, а количественным — контролируемый размер детали.

Иногда проводят сплошное обследование, т. е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяется сравнительно редко.

Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.

Обычно совокупность исследуется относительно некоторого качественного или количественного признака, характеризующего эти объекты. Определим основные понятия математической статистики.

Определение Генеральная совокупность –- полное множество некоторых единиц, которые обладают теми или иными общими свойствами, существенными для их характеристики.

В математической статистике понятие генеральной совокупности трактуется как совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данном реальном комплексе условий и аналогично понятию случайной величины.

Определение Выборочной совокупностью, или просто

выборкой, называют совокупность случайно отобранных объектов.

Определение Объем генеральной совокупности N и объем выборки n – число объектов в рассматриваемой совокупности.

Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности выносить суждение

освойствах в целом.

169

Пример Из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N 1000 , а объем выборки n 100 .

Исследуемый признак генеральной совокупности является дискретным, если он принимает отдельные, изолированные возможные значения с определѐнными вероятностями.

Исследуемый признак генеральной совокупности является непрерывным, если он может принимать все значения из некоторого конечного или бесконечного промежутка.

По всякой ли выборке можно достаточно уверенно судить об генеральной совокупности?

Случайная выборка строится таким образом, что

каждый объект генеральной совокупности имеет одинаковую вероятность быть отобранным;

объекты выбирают независимо друг от друга.

случайность гарантирует надежность.

показывающие, сколько раз встречается то или иное значение признака

 Определение Относительные частоты - отношение частот к объему

wi nni

170