Лекции по математике. Теория вероятности

1,3 1 0,37 0,819 и 1,3 1 0,37 1,781 .

Итак, 0,819 1,781 с вероятностью 0,95 .

Контрольные вопросы

1.Запишите доверительный интервал для оценки математического ожидания .

2.От каких величин зависит точность оценки математического ожидания?

3.Напишите доверительный интервал для оценки среднее квадратическое отклонение нормально распределенного количественного признака Х.

241

Лекция 17

Случайные процессы и их характеристики

Сигналы, способные передать получателю какие-либо сведения, заранее не могут быть известными и представляют собой случайный процесс (последовательность импульсов в системе телеграфной связи или некоторую непрерывную функцию при передаче телефонных сообщений).

Определение Теория случайных процессов-

математическая наука, изучающая случайные явления в динамике их развития.

Определение Случайные сигналы (процессы)- сигналы,

математическим описанием которых являются случайные функции времени.

Пример Случайный процесс - флуктуационные шумы в радиотехнических устройствах. При наблюдении теплового напряжения на выходах идентичных устройств обнаруживается, что функции времени, описывающие эти напряжения, различны. Объясняется же это тем, что в любой момент времени ток в цепи обусловлен большим, но случайным числом вылетающих электронов.

Реальные информационные сигналы носят случайный характер, т.к. ряд их параметров меняется во времени случайным образом. Поэтому случайные сигналы (или случайные процессы) описываются статистическими (вероятностными) законами.

С практической точки зрения решение о случайности или детерминированности процесса основывается на способности воспроизвести процесс в ходе контролируемого эксперимента. Если это приводит к одним и тем же результатам – то процесс считается детерминированным.

Марков Андрей Андреевич (1856-1922) русский математик,

является основоположником теории случайных процессов. Существенно расширил сферу применения закона больших чисел и центральной предельной теоремы.

242

Классификация случайных процессов

Различают следующие случайные процессы:

 Определение Детерминированные процессы – процессы,

которые можно описать математическими формулами (т.е. мы можем определить положение системы в любой момент времени).

Пример Движение спутника на околоземной орбите, измерение температуры воды при нагревании - детерминированные процессы.

Апроцессы, такие как высота волн при шторме, напряжение

внашей электросети, изменение численности жителей в Самаре с течением времени не являются детерминированными – точное положение системы в таких процессах точно определить невозможно.

243

Для описания этих процессов требуются вероятностные понятия и статистические характеристики.

Есть еще один вид процессов - хаотические.

 Определение Хаотические случайные процессы –

детерминированные, нелинейные, с сильной зависимостью от начальных условий.

В реальности начальные условия точно повторить нельзя, и поведение системы через некоторое время становится непредсказуемым. На выходе такие системы имеют случайные характеристики и к ним требуются вероятностные подходы.

Случайные процессы являются математическими моделями для описания случайных явлений, развивающихся во времени. При этом предполагается, что состояние в текущий момент времени есть случайная величина (t, w) .

На пространстве элементарных событий определена - алгебра его подмножеств F и для любого события A F определена его вероятность P( A) . Таким образом задано

вероятностное пространство , F, P .

 Определение Случайный процесс - семейство случайных величин { (t, w)} , определѐнных на , F, P , где под

параметром t понимается время.

Пусть t0 - фиксированный момент.

 Определение Сечение случайного процесса в точке t0 -

244

превращается процесс в результате испытания) называется реализацией (траекторией, выборочной функцией) случайного процесса.

С реализациями мы чаще всего имеем дело на практике. Таким образом, случайный процесс можно рассматривать как совокупность всех возможных его реализаций.

Случайные процессы классифицируют в

зависимости от непрерывности или дискретности и t :

Определение Случайный процесс называется процессом

сдискретным временем (или случайной последовательностью) если система, в которой он протекает, может менять своѐ состояние в дискретные моменты времени.

Пример Студент накупил лотерейных билетов. Выигрыши происходят в определѐнные дни. Случайный процесс

t - число билетов, выигравших до момента времени t .

Определение Случайный процесс называется процессом

снепрерывным временем, если переходы системы могут происходить в любой момент t .

Определение Случайный процесс называется процессом

сдискретными состояниями, если в любой момент времени множество его состояний конечно или счѐтно (если любое его сечение – дискретная случайная величина).

245

устройства в момент времени t .

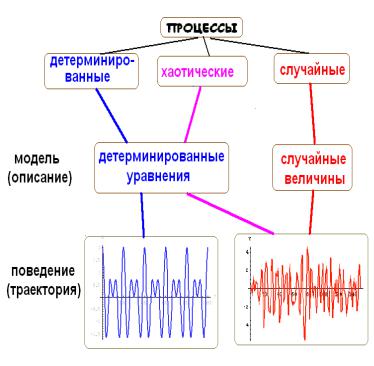
Определение Случайный процесс называется процессом

снепрерывными состояниями, если множество его состояний несчѐтно (если любое его сечение – непрерывная случайная величина).

Законы распределения случайного процесса

Универсальной, исчерпывающей характеристикой случайная величины является еѐ функция распределения

F (x) P( x) .

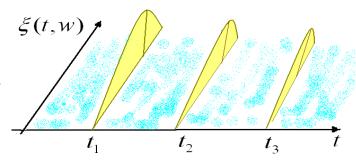
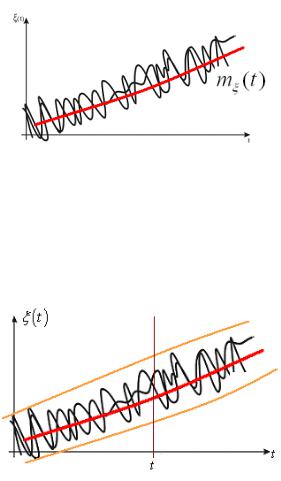
При любом фиксированном t получим сечение случайного процесса. Это случайная величина, которая имеет закон распределения.

F (x, t) P( (t) x) - одномерный закон распределения. Функция зависит от двух аргументов t, x .

Является ли F (t, x) исчерпывающей характеристикой? Нет,

так как характеризует свойства одного отдельного сечения. Двумерный закон распределения

F (x1 , t1 , x2 , t2 ) P( (t1 ) x1 , (t2 ) x2 )

- функция 4-х аргументов.

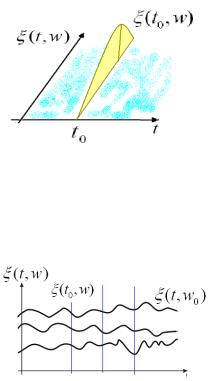
Теоретически число сечений можно увеличивать неограниченно. Однако на практике очень часто вполне можно ограничиться двумерным законом. В общем случае мы имеем n

сечений. Пусть t - случайный процесс и задано некоторое

произвольное множество моментов времени.

Соответствующая совокупность случайных величин(t1 ), ..., (tn ) имеет n – мерную функцию распределения:

F (x1 , ..., xn , t1 , ..., tn ) P{ (t1 ) x1 , ..., (tn ) xn }

246

Семейство конечномерных распределений случайного процесса – это совокупность n -мерных функций распределения для различных n и моментов t .

Семейство конечномерных распределений является основной характеристикой случайного процесса, полностью определяющей его свойства. Говорят, что случайный процесс, задан, если задано его семейство конечномерных распределений.

Моментные характеристики случайного процесса

Функции распределения достаточно полно характеризуют случайный процесс. Однако часто она оказывается довольно сложная или требует для своего определения обработки большого числа экспериментальных данных. Кроме того, часто подробного описания процесса не требуется.

Потому в этих случаях ограничиваются при описании процессов лишь некоторыми числовыми характеристиками.

К ним относятся средние значения, дисперсии и корреляционные функции. Числовые характеристики случайных процессов аналогичны числовым характеристикам случайных величин, которые используются в теории вероятностей, но имеют ту особенность, что представляют собой в общем случае не числа, а функции времени.

Для характеристики случайной величины определяют неслучайные числовые характеристики – математическое ожидание M [ ] - среднее значение случайной величины;

корреляционный момент COV[ , ] M ( M )( M ) , который характеризует степень линейной зависимости между случайными величинами и .

 Определение Неслучайная функция m t , которая t

равна математическому ожиданию соответствующего сечения случайного процесса, называется математическим ожиданием случайного процесса.

mt M t

247

Его можно найти через одномерный закон распределения.

m (t) xp (x, t)dx .

 Определение Дисперсия случайного процесса – это неслучайная функция, которая t равна дисперсии соответствующего сечения.

D (t) D[ (t)] M [( (t) M (t))2 ]

- можно найти через одномерный закон распределения.

D (t) x2 p (x, t)dx m2 (t) .

Математическое ожидание M [ (t)] и дисперсия D[ (t)] важны, но не характеризуют внутреннюю структуру процессов.

248

ожидание и дисперсию.

Решение

Реализации процесса:

mx t M a t am t , Dx t D a t D a D t a2 2 .

Замечание дисперсия определяет степень разброса значений случайного процесса около среднего значения.

Замечание Математическое ожидание и дисперсия характеризуют поведение случайного процесса в отдельные моменты времени.

Корреляционная функция

В качестве характеристики, учитывающей статистическую зависимость между значениями случайного процесса в различные моменты времени, используется корреляционная функция случайного процесса определяемая как

 Определение Корреляционная функция случайного процесса - неслучайная функция равная математическому ожиданию от произведения значений процесса в два различных момента времени.

K (t1 , t2 ) M[( (t1 ) m (t1 ))( (t2 ) m (t2 )] M [( (t1 ) (t2 )] m (t1 )m (t2 )

249

Корреляционная функция – функция двух аргументов - для каждой пары чисел t1 и t2 равна

корреляционному

моменту соответствующих сечений и характеризует степень их линейной зависимости.

Для расчѐта корреляционной функции необходимо знать двумерное распределение.

K (t1 , t2 ) (x1 m (t1 ))(x2 m (t2 )) p (x1 , x2 , t1 , t2 )dx1 , dx2

Корреляционная функция определяет степень линейной зависимости между значениями случайного процесса в различные моменты времени.

Основные свойства корреляционной функции

1.При равенстве аргументов t1 t2 t

K (t, t) D (t)

2. Корреляционная функция симметрична относительно своих аргументов

K (t1 , t2 ) K (t2 , t1 )

т.е. она является симметричной относительно начала отсчета времени.

3. Модуль корреляционной функции не превосходит произведение среднеквадратичных отклонений соответствующих сечений

K (t1 , t2 ) 2 D (t1 )D (t2 )

функцию

250