
Лекции по математике. Теория вероятности
.pdf7.Равномерно распределенная случайная величина Х задана плотностью распределения f(x)= 1/(2l) в интервале (а-1, а+l); вне этого интервала f(x)=0. Найти математическое ожидание и дисперсию X.
8.Диаметр круга х измерен приближенно, причем а<x<b. Рассматривая диаметр как случайную величину X, распределенную равномерно в интервале {а, b), найти математическое ожидание и дисперсию площади круга.
9.Ребро куба х измерено приближѐнно, причѐм a<x<b. Рассматривая ребро куба как случайную величину Х, распределѐнную равномерно в интервале (a,b), найти математическое ожидание и дисперсию объѐма куба.
10.Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая
0,02А.
101
Лекция 7
Основные законы непрерывных случайных величин
В теории и практике надежности чаще всего используются следующие законы распределения:
равномерный закон распределения
нормальный (Гаусса),
логарифмически нормальный,
Вейбулла,
экспоненциальный (показательный) и др.
Равномерный закон распределения
Часто на практике мы имеем дело со случайными величинами, распределенными определенным типовым образом, то есть такими, закон распределения которых имеет некоторую стандартную форму. В лекции 8 были рассмотрены примеры таких законов распределения для дискретных случайных величин (биномиальный и Пуассона).
Для непрерывных случайных величин тоже существуют часто встречающиеся виды закона распределения, и в качестве первого из них рассмотрим равномерный закон.
Определение Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение
const, при a x b |
|
|
f x |
при x a, x b |
,. |
0, |
|
|
Для того чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри
102
этого интервала значения этой случайной величины были бы |
|||||
равновероятны. |
|
|
|
|
|
Найдем значение, которое принимает f x при x a,b |
|||||
Из условия нормировки следует, что |
|||||
b |
|
b |
|
|
|
f x dx cdx c b a 1 |
|||||
a |
|
a |
|
|
|
Откуда f x c |
1 |
. |
|
|
|
|
|
|
|
||
b a |
|
|
|||
|
|
|
|
|
|
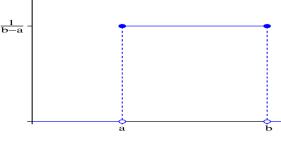
Плотность равномерного распределения имеет вид: |
|||||
|
|
|
1 |
, x a, b |
|
|
f x |
|
|
|
|
|
|
a |
|||
|
b |
|
|||
|
|
0, x a, b |
|||
|
|
|
|
|
|
Непрерывное равномерное распределение характеризуется тем, что вероятность любого интервала зависит только от его длины.
График плотности распределения |
|
|
||||||||
Вероятность попадания |
равномерно |
распределенной |
||||||||
|
|
|
|
|
, |
|
( |
b |
) |
|
случайной величины на интервал |
|
|
a Ј a < b Ј |
|
||||||
|
|
|
|
|
|
|
||||
равна при этом |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
dx |
|
|
|
|
|||||
|
|
. |
|
|
|
|
||||
b a |
b a |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
P x b a
103
Замечание Равномерное распределение непрерывный аналог дискретного распределения вероятностей для опытов с равновероятными исходами.
Вид функции распределения для нормального закона:
0, x a |
|||
|
a |
|
|
x |
|
||
F x |
|
|
, a x b |
|
a |
||
b |
|
||
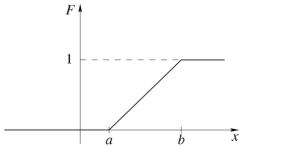
1, x b
График функции распределения равномерной случайной величины
 Пример Автобусы некоторого маршрута идут с интервалом 5 минут. Найти вероятность того, что пришедшему на остановку пассажиру придется ожидать автобуса не более 2 минут.
Пример Автобусы некоторого маршрута идут с интервалом 5 минут. Найти вероятность того, что пришедшему на остановку пассажиру придется ожидать автобуса не более 2 минут.
Решение
Время ожидания является случайной величиной, равномерно распределенной в интервале [0, 5].
Тогда |
1 |
|
2 |
|
|||
|
|
|
|
|
|
||
f x 5 |
, p 0 |
x 2 5 |
0.4 . |
||||
|
|||||||
Замечание Случайная величина имеет непрерывную строго возрастающую функцию распределения.
Замечание Случайная величина, распределенная по равномерному распределению имеет практическое применение в имитационном моделировании, выступая основой генерирования любых случайных величин, потоков и случайных процессов.
104
Математическое ожидание и дисперсия случайной величины, распределенной по равномерному закону
По определению вычислим математическое ожидание:
M X v |
xf x dx b |
|
x |
|
|
dx |
b2 a2 |
|
a b |
||||||||||||
|
|
|
|
2 b a |
|
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
b a |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
M X |
a b |
|
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 f x dx |
1 |
|
|
b |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M ( X 2 ) v |
b a |
x2dx |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b3 a3 |
|
|
|
b2 ba a2 |
|
|
|
|
|
|
|
|
|
|
||||||
3 b a |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
D( X ) |
2 |
M ( X 2 ) M 2 ( X ) |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
b2 ba a2 |
|
|
a2 2ba b2 |
b a 2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
12 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
или
D( X ) b a 2
12
Замечание Мода равномерного распределения – любое число из отрезка a,b
Замечание Коэффициент ассиметрии равен нулю
Замечание Коэффициент эксцесса равен -6/5.
Замечание Медиана совпадает с математическим ожиданием.
105
Экспоненциальное распределение
Экспоненциальное распределение является одним из основных распределений, используемых в теории надежности.
Например, продолжительность безотказной работы многих технических устройств, а также время задержки вылета самолѐта по вине технических служб аэропорта удовлетворительно описываются соответствующими экспоненциальными распределениями.
Экспоненциальное распределение описывает наработку до отказа объектов, у которых в результате сдаточных испытаний отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации.
Экспоненциальный закон характерен для распределения случайных величин, изменение которых обусловлено влиянием доминирующего фактора. Он используется при рассмотрении внезапных отказов деталей в тех случаях, когда явления изнашивания и усталости выражены настолько слабо, что ими можно пренебречь.
Определение Случайная величина x имеет экспоненциальное (показательное) распределение с параметром
0 , если плотность распределения . |
|
|
|
f x |
e x , x 0 |
||
|
|
x 0 |
|
|
0, |
|
|
Функция распределения |
|
|
|
0, |
при |
x 0 |
|
F (x) 1 e x при |
x 0 |
||
|
|
|
|
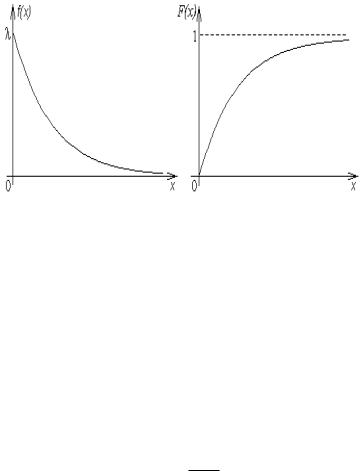
Графически функция плотности и функция распределения экспоненциального распределения имеет вид представленный ниже.
106
Математическое ожидание и дисперсия |
|
|
|
|
|||
|
|
u x; |
e xdx dv; |
|
|||
|
|
|
|
|
|
||
M (X ) |
|
|
|
|
|
||
xf (x)dx x e xd |
|
|
e x |
|
|
||
|
0 |
du dx; |
|
|
v; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
xe |
x |
|
e |
x |
|
|
|
|
|
e |
x |
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
e xdx |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
0 |
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|||||||||
Следовательно, окончательно имеем |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
M ( X ) |
1 |
; |
D( X ) |
1 |
; x |
|
1 |
. |
|||||||||
|
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Замечание Коэффициент ассиметрии равен 2. Замечание Коэффициент эксцесса равен 6.
Замечание Медиана равна ln 2 .
Замечание Экспоненциального распределения имеет одинаковое математическое ожидание и среднее квадратичное отклонение.
Вероятность попадания случайной величины в заданный интервал.
P(a x b) F (b) F (a) e a e b .
107
Задачи для самостоятельного решения
1.Непрерывная случайная величина Х распределена по
показательному закону, заданному плотностью вероятности
f ( x ) 3e 3x при |
x 0 ; |
f ( x ) 0 при |
x 0 . Найти |
вероятность того, что в результате испытания Х попадает в интервал (0.13, 0.7).
2. Непрерывная случайная величина Х распределена по показательному закону, заданному при x 0 плотностью
распределения f ( x ) 0.04e 0.04 x ; при |
x 0 функцией |
f ( x ) 0 . Найти вероятность того, что в результате испытания Х попадает в интервал (1, 2).
3.Непрерывная случайная величина Х распределена по
показательному |
закону, |
заданному |
функцией распределения |
|
F( x ) 1 e 0.6 x |
при |
x 0 ; при |
x 0 |
F( x ) 0 . Найти |
вероятность того, что в результате испытания Х попадет в интервал (2, 5).
4.Найти математическое ожидание показательного
распределения f ( x ) e x при x 0 ; f ( x ) 0 при x 0 .
5.Найти математическое ожидание показательного
распределения, |
заданного |
при |
x 0 : а) |
плотностью |
|
f ( x ) 5e 5x ; б) функцией распределения F( x ) 1 e 0.1x . |
|||||
6. |
Найти: |
а) дисперсию; б) |
стандартное |
отклонение |
|
показательного |
распределения, |
заданного |
плотностью |
||
вероятности: f ( x ) e x при x 0 ; f ( x ) 0 при x 0 . |
|||||
7. |
Найти |
дисперсию |
и |
стандартное |
отклонение |
показательного |
распределения, |
заданного |
плотностью |
||
вероятности f ( x ) 10e 10 x при x 0 . |
|
||||
8.Найти дисперсию и стандартное отклонение
показательного закона, заданного функцией распределения
F( x ) 1 e 0.4 x при x 0 .
108
Закон Вейбулла
Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для них характерны три вида зависимостей интенсивности отказов от времени, соответствующих трем периодам жизни этих устройств
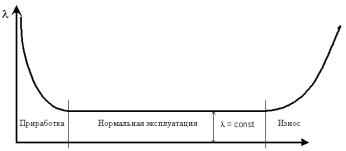 Интен сивность отказов монотонно убывает (период приработки),
Интен сивность отказов монотонно убывает (период приработки),
монотонно возрастает (период износа). Распределение Вейбулла - двухпараметрическое семейство
абсолютно непрерывных распределений.
Распределение Вейбулла достаточно близко подходит для ряда механических объектов (к примеру, шарикоподшипников), оно может быть использовано при ускоренных испытаниях объектов в форсированном режиме
Определение Случайная величина X имеет
распределение Вейбулла с параметрами m и a , если плотность распределения
|
|
|
|
|
|
|
|
|
|
|
x m |
|
|
|
|
f x |
m |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
xm 1e |
|
|
a |
|
|
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
Функция распределения имеет вид: |
|
|
|
|
|
|||||||||
F x |
x |
|
|
t dt |
|
|
|
x |
|
|
||||
|
f |
x |
1 |
e |
|
|
|
|
, x 0 |
|||||
x |
|
|
|
|
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
0, x |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
109
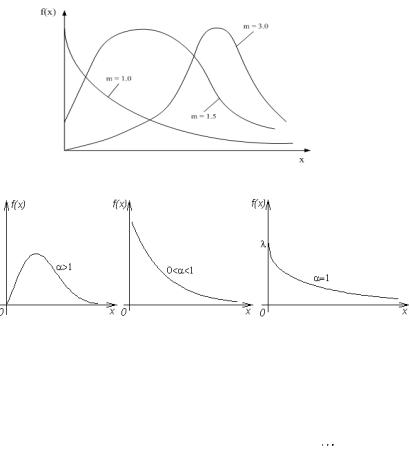
Плотность с различными значениями m имеет вид:
Плотность с различными значениями a имеет вид:
Замечание Значение параметра m зависит от коэффициента вариации и определяется по таблицам, расчетом или графоаналитическим путем. Величина его влияет на форму дифференциальной кривой.
При m 1 распределение |
Вейбулла |
преобразуется |
в |
|||
экспоненциальное, |
при |
m 2,5 3,5 и |
a 0,3 |
0,4 |
— |
|
приближается к нормальному. |
|
|
|
|
||
Замечание |
Если |
a 1, |
то распределение |
Вейбулла |
||
превращается в показательное распределение.
110
