
Лекции по математике. Теория вероятности
.pdf
Пример
За лето на Черноморском побережье было 67 солнечных дней. Какова частота солнечных дней на побережье за лето? Частота пасмурных дней?
Решение
1. |
W A |
|
67 |
0.728 |
частота солнечных |
дней на |
||
92 |
||||||||
|
|
|
|
|||||
побережье за |
лето, W B |
25 |
0.272 - частота |
пасмурных |
||||
92 |
||||||||
|
|
|
|
|
|
|
||
дней.
Условная вероятность
Пусть имеем два последовательных случайных событий, то какова вероятность наступления второго события, если первое событие уже произошло.
Пример
Пусть в урне было 5 шаров, (2 белых+ 3 черных).
Найти вероятность извлечь белый шар во втором испытании.
Решение
После извлечения первого шара в ней останется 4 шара
и один белый в их числе (если извлекли белый)
или 2 белых ( если в первый раз извлечен не белый шар).
Впервом случае вероятность извлечь белый шар во второй
раз будет 14 , во втором 12 .
Таким образом вероятность извлечь белый шар во втором испытании зависит от результата первого испытания.
Понятия условной вероятности и независимости введены
А.Муавром в 1718 г. Абрахам де Муавр (1667 -1754) —
английский математик французского происхождения. Провѐл вероятностное исследование азартных игр.
Определение Условная вероятность- вероятность одного события, вычисленная в предположении, что другое событие произошло.
31

Вероятность события A1 в предположении, что произошло событие A2 обозначаем P A1 / A2
Определение Два события называются независимыми, если вероятность появления каждого из них не зависит от того, имели ли место другие.
Определение Два события называются зависимыми, если появление одного из них влияет на вероятность наступления другого
A1 / A2 P A1 , то говорят, что A1 независимо от
A2 , т.к. его вероятность не зависит от того, произошло ли событие A2 или нет.
Аналогично, если P A2 / A1 P A2 , то говорят, что A2
независимо от A1
Независимость двух событий – свойство симметричное.
Пример
A – извлечение из колоды туза, B – то, что и вторая вынутая из колоды карта туз. Тогда, если после первого раза карта была возвращена в колоду, то вероятность вынуть вторично туз не меняется:
P B P A 324 18 0.125
Если же первая карта в колоду не возвращается, то осуществление события A приводит к тому, что в колоде осталась 31 карта, из которых только 3 туза.
Поэтому
|
B |
|
3 |
|
0.097 . |
|
P |
|
|
|
|
||
|
|
|
||||
|
A |
|
31 |
|
||
 Пример К экзамену надо подготовить 25 вопросов. Студент пришел на экзамен, зная 20. Какова вероятность того, что студент ответит на все три вопроса билета?
Пример К экзамену надо подготовить 25 вопросов. Студент пришел на экзамен, зная 20. Какова вероятность того, что студент ответит на все три вопроса билета?
Решение
Пусть события: A – студент знает первый вопрос;
32
B– студент знает второй вопрос;
C– студент знает третий вопрос. Тогда нужная вероятность будет
P ABC P A P |
B |
P C.AB |
20 |
|
19 |
|
18 |
|
57 |
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
25 24 23 |
115 |
|
||||||
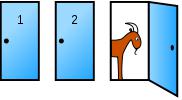
Парадокс Монти Холла
Задача формулируется как описание гипотетической игры, основанной на американском телешоу «Let’s Make a Deal», и
названа в честь ведущего этой передачи.
Вы стали участником игры, в которой нужно выбрать одну из трех дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы.
Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза.
Вопрос: не желаете ли вы изменить свой выбор и выбрать дверь номер 2.
Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Решение
Построим дерево принятия решений.
33
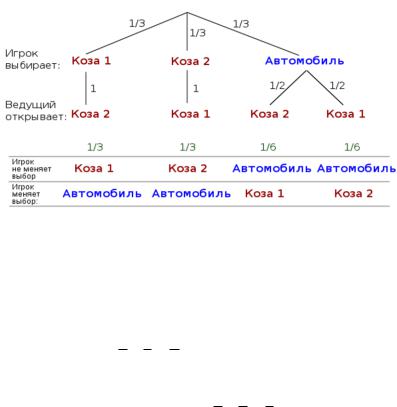
Когда игрок сначала выбрал дверь, за которой находится коза, изменение выбора приводит к выигрышу.
В двух последних случаях, когда игрок сначала выбрал дверь
савтомобилем, изменение выбора приводит к проигрышу. Суммарная вероятность того, что изменение выбора
приведѐт к выигрышу, эквивалентна сумме вероятностей первых двух исходов, то есть 13 13 23 .
Соответственно, вероятность того, что отказ от изменения выбора приведѐт к выигрышу, равна 16 16 13
Вывод Изменение первоначального выбора приводит к выигрышу в двух случаях из трѐх в среднем!!!!
Контрольные вопросы
2.Дайте статическое определение вероятности.
3.В чем отличие от классического определения вероятности В чем разница абсолютной и относительной частоты?
34

Задачи для самостоятельно решения
1. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.
Отв. p 0.1.
2.Брошена игральная кость. Найти вероятность того, что выйдет четное число очков. Отв. p 0.5 .
3.Участники жеребьевки тянут из ящика жетоны с номерами
от 1 до 100. Найти вероятность того, что номер первого, наудачу извлеченного жетона, не "содержит цифры 5. Отв. p 0.81.
4.В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному из расположенных «в одну линию» кубиках можно будет прочесть
слово «спорт». Отв. p 1201 .
5.На каждой из шести одинаковых карточек напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны, Найти вероятность того, что на четырех, вынутых по одной и расположенных «в одну линию» карточках, можно будет прочесть слово «трос» Отв. `p = 1/А_6^4=1/360.
6.Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней: а) одну; б) две; в) три.
Отв. а) 0,384; б) 0,096; в) 0,008.
7.Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если первая кость: а) оказалась дублем, б) не есть дубль. Отв. (а)
92 (б) 94
8. В замке на общей оси пять дисков, каждый из которых разделен на шесть секторов с различными написанными на них
35
буквами. Замок открывается, только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть Отв. `р =1/6^5`.
9.Восемь различных книг расставляются наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом. Отв. 0.25
10.Библиотечка состоит из десяти различных книг, причем пять книг стоят по 4 рубля каждая, три книги — по одному рублю и две книги — по 3 рубля Найти вероятность того, что
взятые наудачу две книги стоят 5 рублей. Отв. 5 /12 ` 11. В партии из 100 детален отдел технического контроля
обнаружил 6 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей?Отв. w 0.06 .
12. При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85 Найти число попаданий, если всего было произведено 120 выстрелов. Отв. 102 попадания.
36
Лекция 3
Алгебра событий - сумма двух событий
Определение Суммой двух событий A1 и A2 -
называется событие, состоящее в появлении хотя бы одного из этих событий.
A A1 A2
Теорема Вероятность суммы двух несовместных событий равняется сумме их вероятностей.
P A1 A2 P A1 P A2
Если события A1 и A2 взаимно не исключают друг друга, то
теорема будет другая.
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
|
n |
|
n |
|
|
|
P Ai |
P |
Ai |
||
i 1 |
|
i 1 |
|
Следствие теоремы сложения Сумма вероятностей полной группы несовместимых событий равна единице.
Доказательство
Пусть несовместимые события A, B, C, , N - образуют
полную группу событий, следовательно они единственно возможные и несовместные.
При испытании хотя бы одно их этих событий появится, т.к. оно достоверно
P A 1 или Р B 1 или Р N 1
но события по условию являются несовместимыми и следовательно, на основании теоремы сложения что и т.д.
Алгебра событий – произведение двух событий
Определение Произведением нескольких событий называется событие, состоящие в совместном наступлении всех этих событий в результате испытания. Обозначают
A B, A B, A и B
37
Замечание Произведение означает союз «и» (АВС, это означает, что наступило событие A и B и C ).
 Пример A – «из колоды карт вынута дама», B – «из колоды карт вынута карта пиковой масти». A B означает «вынута дама пик».
Пример A – «из колоды карт вынута дама», B – «из колоды карт вынута карта пиковой масти». A B означает «вынута дама пик».
 Пример A – « число выпавших очков < 5», B – «число выпавших очков > 2», C – «число выпавших очков четное». Тогда A B C – «выпало 4 очка».
Пример A – « число выпавших очков < 5», B – «число выпавших очков > 2», C – «число выпавших очков четное». Тогда A B C – «выпало 4 очка».
Теорема Вероятность суммы двух совместных событий равняется сумме их вероятностей, уменьшенная на вероятность произведения этих событий.
P A1 A2 P A1 P A2 P A1 A2
Теорема Вероятность произведения взаимно независимых событий равна произведению их вероятностей.
P A1 A2 P A1 P A2 .
Теорема Вероятность произведения зависимых событий равна произведению вероятности одного события на условную вероятность другого события, вычисленную в предположении, что первое случайное событие уже произошло
P A 1 A 2 P A 1 P A 2 P A 1 A 2
Свойства операций сложения и умножения
1.A B B A коммутативность сложения.
2.A B C A B C - ассоциативность сложения.
3.A B B A коммутативность умножения.
4.A B C A B C ассоциативность умножения
5.A B C A B A C закон дистрибутивности.
38

Вероятность появления хотя бы одного из событий
Теорема Вероятность появления хотя бы одного из событий A1, A2 , , An , независимых в совокупности, равна
разности между единицей и произведением вероятностей противоположных событий
P A 1 P A1 P A2 P An 1 q1 q2 qn
Следствие. При производимых n одинаковых
независимых испытаниях, в каждом из которых события A появляется с вероятностью p , вероятность появления
события A хотя бы один раз равна
P A 1 1 p n
 Пример В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Пример В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Решение
Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие A )
P A 1030 13
Вероятность появления синего шара (событие B )
P B 305 16
События A и B несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность
P A B P A P B 13 16 12
 Пример На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.
Пример На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.
Решение
39

Первый способ. Пусть события A – хотя бы один учебник в
переплете; |
B – один из взятых учебников в переплете, два – без |
||||||||||||||||||
переплета; |
C – два в переплете, один без переплета; D – все |
||||||||||||||||||
три учебника в переплете. |
|
|
|
|
|
|
|
|
|
|
|||||||||
Очевидно, |
A B C D . |
|
|
|
|
|
|
|
|
|
|||||||||
Найдем вероятности событий B , C , и D . |
|
|
|
|
|
|
|||||||||||||
|
|
|
C51C102 |
|
|
45 |
, |
|
|
|
C52 C101 |
20 |
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P(B) |
|
|
C 3 |
|
91 |
P(C) |
|
C 3 |
91 |
||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
C53 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
||
P(D) C 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
91 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
67 |
. |
|
|
|
|
|
|
|
|
P( A) P(B) P(C) P(D) 91 |
|
|
|
|
|
|
|||||||||||
Второй |
|
способ. |
Вновь A |
– хотя бы один |
учебник в |
||||||||||||||
переплете; A - ни один из взятых учебников не имеет переплета.
Так как события A и A противоположные, то
|
|
|
C103 |
|
24 |
|
67 |
|
|
P( A) 1 P( A) 1 |
1 |
|
. |
||||||
C 3 |
91 |
91 |
|||||||
15 |
|
|
|
|
|||||
|
|
|
|
|
|||||
 Пример Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках;
Пример Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках;
Решение
A – формула содержится в одномсправочнике;
B – формула содержится в двух справочниках; Воспользуемся теоремами сложения и умножения
вероятностей.
P ABC ABC ABC P ABC P ABC P ABC0,6 0,3 0,2 0,4 0,7 0,2 0,4 0,3 0,8 0,188
P ABC ABC ABC 0,6 0,7 0,2 0,6 0,3 0,8 0,4 0,7 0,8 0,452
40
