Лекции по математике. Теория вероятности

Нормальное распределение (закон Гаусса)

Нормальное распределение играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это—наиболее часто встречающийся на практике закон распределения.

Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Нормальное распределение имеет очень широкое распространение в прикладных задачах. Это связано с тем, что в реальной жизни многие исследуемые случайные величины являются следствием различных случайных событий.

Рост людей на нашей планете хорошо описывается нормальным распределением. Это, по-видимому, связано с тем, что на рост влияют разнообразные независимые случайные факторы: климат, экология окружающей среды, экономические условия, болезни и т.д. Хотя, конечно, "бесконечно" большие люди (великаны) и "бесконечно" маленькие люди (гномы) бывают только в сказках. Это говорит о том, что "хвосты" истинного распределения роста людей отличаются от нормального распределения.

В частности, при достаточно общих предположениях сумма большого числа независимых СВ имеет распределение близкое к нормальному.

Часто нормальное распределение называют распределением Гаусса (Карл Фридрих Гаусс (1777-1855), или Муавра, в честь тех, кто, как считается, открыл его и, веком ранее, что не так достоверно, Авраам де Муавр (1667-1754). Термин был впервые использован Гальтоном в 1889 г.

CВ подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Такая ситуация распространена, поэтому в природе чаще всего

111

встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Нормальный закон наблюдается, когда на измеряемую случайную величину действуют разнообразные факторы, не связанные между собой и равнозначно действующие на случайную величину.

Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым

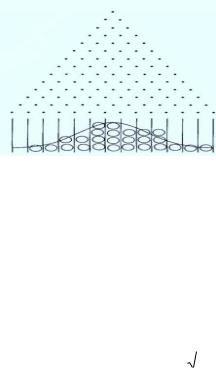
Доска Гальтона

Доска Гальтона -вертикально установленная доска в форме равнобедренного треугольника.

В доске расположены колышки, один в верхнем ряду, два во втором, и так далее. Каждый последующий ряд имеет на один колышек больше. Колышки в сечении треугольные, так что, когда падает шарик, у него есть вероятность 50/50 пойти вправо или влево.

В основании доски находится серия желобов для подсчета попаданий каждого броска.

Шарики, падающие через доску Гальтона и достигающие желобов, начинают формировать нормальное распределение.

Чем «глубже» доска (то есть чем больше рядов она имеет) и чем больше шариков бросается, тем больше конечный результат будет напоминать нормальное распределение.

 Определение Нормальное распределение (гауссовское)

определяется функцией плотности следующим образом

где a – математическое ожидание.

112

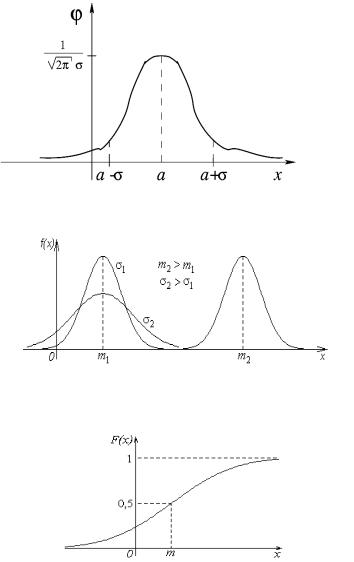
Нормальный закон - это двухпараметрический закон, для записи которого нужно знать математическое ожидание и среднее квадратичное отклонение. Нормальное распределение зависит от двух параметров — смещения и масштаба

График плотности нормального распределения называется

нормальной кривой или кривой Гаусса

Функция плотности при различных значениях параметров

 Замечание Графики плотности нормального распределения, имеют единственный максимум в точке x m .

Функция распределения имеет вид:

113

y x m , dy 1 dx

x m

Нормальная кривая обладает следующими свойствами:

1)Функция определена на всей числовой оси.

2)При всех x функция распределения принимает только положительные значения.

3)Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по

абсолютной величине аргумента x , значение функции стремится

кнулю.

4)Найдем экстремум функции.

5)Функция является симметричной относительно прямой

xa , т.к. разность x a входит в функцию плотности

распределения в квадрате.

6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.

114

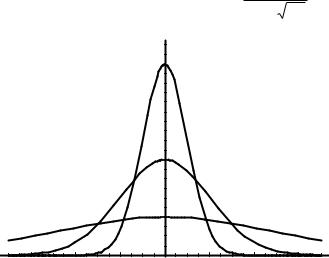
Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения 1, 2 и 7 .

Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное

распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1 -

N0,1 .

Замечание Нормальное распределение формируется под влиянием большого числа случайных факторов, служит хорошим приближением для построения математических моделей.

115

Функция Лапласа.

Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

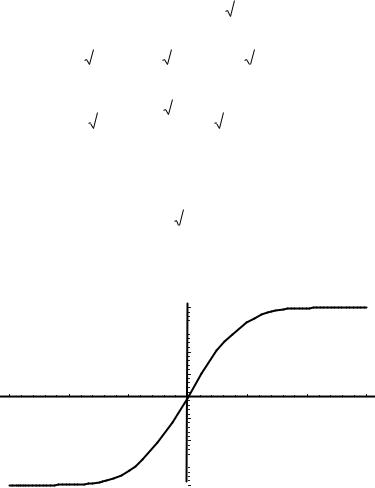
которая называется функцией Лапласа или интегралом вероятностей.

Ниже показан график функции Лапласа.

1

0.75 0.5 0.25

-0.25 -0.5 -0.75

-1

116

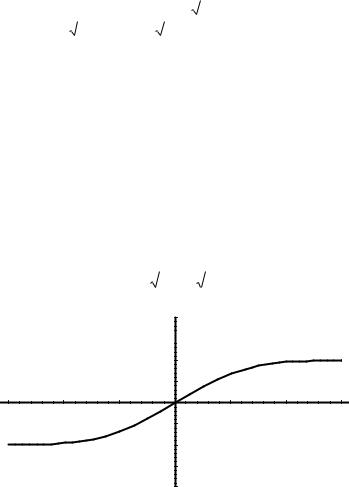
Свойства функции Лапласа

1.Ф x определена при всех значениях х.

2.Ф(0)=0.

6.Ф x – функция нечетная: Ф x = –Ф x .

Значения этой функции при различных значениях x посчитаны и приводятся в специальных таблицах, приведены в приложении. Функцию Лапласа также называют функцией ошибок и обозначают erf x .

Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:

Ниже показан график нормированной функции Лапласа.

1

0.75 0.5 0.25

-0.25 -0.5 -0.75

-1

 Замечание Математическое ожидание, мода и медиана совпадают и равны математическому ожиданию.

117

 Замечание Коэффициент ассиметрии и коэффициент эксцесса равны 0.

Правило трех сигм

Нормально распределенная случайная величина с большой вероятностью принимает значения, близкие к своему математическому ожиданию.

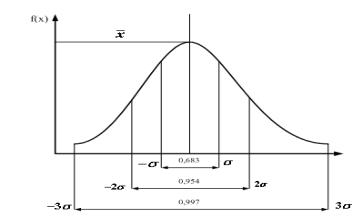
Величина X (среднее арифметическое) показывает смещение кривой f x вдоль оси абсцисс без изменения ее

формы, т. е. расстояние от начала координат до абсциссы с максимальной ординатой. Величина (среднее квадратичное отклонение) показывает разброс отдельных значений случайной величины x относительно среднего арифметического.

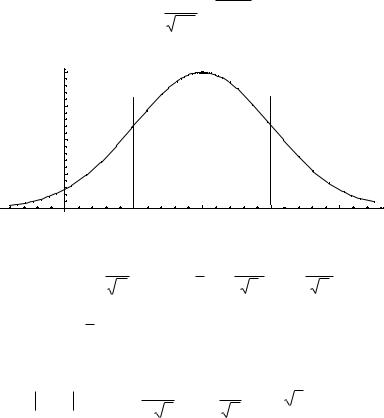
На участке кривой, ограниченной ординатами и расположено 68,3% значений случайной величины; на участке, ограниченном ординатами 2 -95,4%; на участке с ординатами

3 - 99,7%.

Правило трех сигм: вероятность того, что случайная величина x лежит в пределах 3 , близка к единице или к 100%. Следовательно, значения случайной величины, лежащие за пределами 3 - сигм, можно отбросить как промахи.

118

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Правило k :

0.6827, k 1,

P X m k Φ k Φ k 0.9545, k 2,

0.9973, k 3.

Пример Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожидание а = 65 т и средним квадратичным отклонением = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.

Решение

Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100 65 = 6500) не превосходит 6600 – 6500 = 100 т. Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.

Получаем:

Пример. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.

Решение

Плотность распределения имеет вид:

119

1.Верно ли, что математическое ожидание, медиана и мода нормально распределенной НСВ X совпадают.

2.Верно ли, что кривая Гаусса симметрична относительно своего математического ожидания.

3.Верно ли, что кривая Гаусса имеет максимум в точке равной значению M(X).

4.Верно ли, что кривая Гаусса тем круче, чем больше

сигма?

120