
Лекции по математике. Теория вероятности
.pdf
|
Согласно |
гипотезе |
H0 |
отклонение эмпирических частот |
||
|
|
|||||
p* |
ni |
|
|
|
|
|
|
|
теоретических вероятности pi P( Xi ) |
||||
i |
|
n |
от |
|||
|
|
|||||
объясняется случайными причинами. Чтобы проверить правдоподобие этой гипотезы для уровня значимости в качестве меры расхождения между гипотетическим и статистическим распределениями рассчитывается величина
|
k |
(n np )2 |
||
набл2 |
|
i |
i |
. |
|
|
|||
|
i 1 |
|
npi |
|
Эта величина – случайна, т.к. |
в различных опытах она |
|||
принимает различные, заранее неизвестные значения. Чем меньше отличаются теоретические и эмпирические частоты, тем
меньше |
величина критерия, следовательно, |
критерий |
||
2 характеризует |
степень близости |
теоретического и |
||
эмпирического распределений. |
|
|
||
При |
n |
закон распределения |
критерия |
Пирсона |
независимо от того, какому закону подчинена генеральная
совокупность, стремится к закону распределения |
2 с k |
||
степенями свободы. |
|
|
|
Число |
степеней свободы k m r 1 где |
m - |
число |
значений, |
которые принимает случайная величина, |
r – число |
|
параметров предполагаемого теоретического распределения, вычисленных по экспериментальным данным.
Критерий 2 – правосторонний.
Потребуем, чтобы вероятность попадания в критическую область, в предположении справедливости H0 , была равна принятому уровню значимости .
P{ 2 кр2 ( , k)}
По таблице находим кр2 ( , k) и если набл2 кр2 – нет оснований отвергать H0 , если набл2 кр2 – отвергаем гипотезу.
201
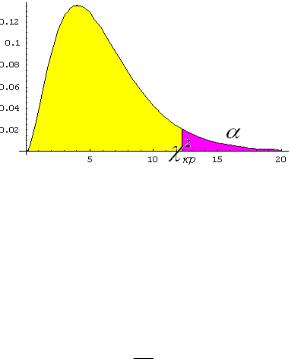
Необходимо, чтобы каждое ni 5 . Если некоторые значения меньше 5, имеет смысл объединить их с соседними.
Замечание |
2 - критерий Пирсона в качестве меры |
расхождения U |
берется 2 , равная сумме квадратов |
отклонений частоты
m
U 2 ci i pi 2
i 1
в качестве весов берут ci n
pi
Схема применения критерия
1.Определяется мера расхождения эмпирических и теоретических частот 2
2.Для выбранного уровня значимости по таблице 2
распределения находят критическое значение ,k 2
3.Если фактически наблюдаемое 2 больше
критического, т.е. |
2 2 |
,k |
, то гипотеза отвергается, |
|
|
|
|
|
|
если 2 |
2 |
то принимается. |
||
|
,k |
|
|
|
202 |
|
|
|
|

Случайная величина
2 |
r |
n |
|
|
|
i |
i 1
характеризует согласованность
n pi 2 n pi
гипотезы Н 0 с опытными
данными.
Схема применения критерия 2 для непрерывных
случайных величин
Пусть проведено n ( n 50 ) независимых опытов, в каждом из которых случайная величина приняла определенное
значение. Все значения упорядочены в виде вариационного ряда. Весь интервал значений делим на S частичных одинаковых интервалов [ai , ai 1 ] и считаем число значений выборки,
попавших в i - тый интервал
Выдвигаем гипотезу H0 , состоящую в том, что случайная величина имеет закон распределения F :
В качестве меры расхождения между гипотетическим и статистическим распределениями рассчитывается величина
|
|
|
k |
(n np )2 |
|
||
|
|
набл2 |
|
i |
i |
, |
|
|
|
|
npi |
|
|||
|
|
|
i 1 |
|
|
|
|
где pi |
P(ai ai 1 ) . |
|
|
|
|
|
|
Число степеней |
свободы |
k m r 1 |
где m - число |
||||
частичных интервалов, на которые |
разбивается выборка, r – |
||||||
число |
параметров |
предполагаемого |
теоретического |
||||
распределения, вычисленных по экспериментальным данным. Задаваясь уровнем значимости, по таблице находим
кр2 ( , k) и |
если набл2 |
кр2 – нет оснований отвергать H0 , если |
|
набл2 |
кр2 |
– отвергаем гипотезу. |
|
Число выборочных значений ni , i 1 r в каждом разряде должно быть не менее 5-10.Если это не выполняется, то разряды
203
надо объединять. В этом случае и соответствующие частоты надо сложить.
 Пример При 4040 бросаниях монеты французский естествоиспытатель Бюффон получил 2048 выпадений герба и 1992 выпадения цифры. На уровне значимости = 0,05 проверим гипотезу о том, что монета была правильной.
Пример При 4040 бросаниях монеты французский естествоиспытатель Бюффон получил 2048 выпадений герба и 1992 выпадения цифры. На уровне значимости = 0,05 проверим гипотезу о том, что монета была правильной.
Решение
Здесь в результате испытания может произойти одно из двух событий — выпадение герба либо выпадение цифры. Поэтому имеем:
A1 = {выпадение герба}, A2 = {выпадение цифры},
n = 4040, m1 = 2048, m2 = 1992. |
|
|
|
|
|
|||||||||
Нулевая гипотеза - H |
|
: p A |
p A |
|
|
|
1 |
, |
||||||
0 |
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т. е. p1 p2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим величину 2 . Имеем: |
|
|
|
|
|
|||||||||
|
2 |
|
m1 np1 2 |
|
m2 np2 |
2 |
|
|
||||||
|
|
np1 |
|
|
np2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2048 2020 2 |
|
1992 2020 2 |
0.776 |
||||||||||
|
|
2020 |
|
|
2020 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
Число степеней свободы k в данном случае равно r 1 2 1 1.
По известным значениям = 0.05, k = 1 находим в таблице
2kp 3.8
Так как 2 2kp , то нулевая гипотеза принимается -
монета была правильной.
 Пример Фирма владеет тремя магазинами. Руководство фирмы решило выяснить, посещают ли покупатели все три магазина одинаково охотно либо имеется некоторое различие. Для проверки была собрана информация о количестве покупателей, сделавших покупки в течение недели. Оказалось,
Пример Фирма владеет тремя магазинами. Руководство фирмы решило выяснить, посещают ли покупатели все три магазина одинаково охотно либо имеется некоторое различие. Для проверки была собрана информация о количестве покупателей, сделавших покупки в течение недели. Оказалось,
204

что в первом магазине это число составляет 160 человек, во втором — 225. в третьем —215.
Решение
Нулевой гипотезой будет равенство вероятностей посещения покупателем первого ( p1 ), второго ( p2 ) и третьего ( p3 )
магазинов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
: |
|
p |
p |
|
p |
|
|
1 |
. |
|
|
0 |
2 |
3 |
|
|
||||||||||
|
|
|
|
1 |
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
В результате испытания получаем |
|
|
|
|
|
|
||||||||
m1 =160, m2 =225, |
m3 =215, |
n =160+225+215=600 |
||||||||||||
Вычислим величину |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
160 200 2 |
|
225 200 2 |
|
215 200 2 |
12.25 |
||||||||
|
|
|
|
|
||||||||||
200 |
|
|
|
200 |
|
|
|
|
200 |
|
||||
Обратимся теперь |
|
к |
таблице |
критических |
значений |
|||||||||
(при k 2 ). Даже на уровне значимости = 0.01 имеем 2kp =
9.2. Таким образом, 2 2kp .
Поэтому, видимо, разницу в посещаемости магазинов в течение недели нельзя объяснить случайными колебаниями.
Пример По выборке из 24 |
вариант выдвинута гипотеза о |
|||
нормальном |
распределении |
генеральной |
совокупности. |
|
Используя |
критерий Пирсона |
при |
уровне |
значимости |
0,025 |
среди заданных значений 2 |
= {34, 35, 36, 37, 38} |
||
указать:
а) наибольшее, для которого нет оснований отвергать гипотезу; б) наименьшее, начиная с которого гипотеза должна быть отвергнута.
Решение
Найдем число степеней свободы k с помощью формулы: k S r 1,
где S - число групп выборки (вариант), r - число параметров распределения.
Так как нормальное распределение имеет 2 параметра ( m и), получаем
205
k 24 2 1 21 .
По таблице критических точек распределения 2 , по заданному уровню значимости 0,025 и числу степеней
свободы k 21 определяем критическую точку кр2 35,5. В случае
|
а) для значений |
2 , равных |
34 и 35, нет оснований |
|
отвергать |
гипотезу о |
нормальном |
распределении, так как |
|
2 |
кр2 |
. А наибольшее среди этих значений 2 35 . |
||
В случае б) для значений 36, 37, 38 гипотезу отвергают, так как
2 кр2 . Наименьшее среди них 2 36 .
Контрольные вопросы
1.Что произойдет со стандартной ошибкой среднего, если размер выборки увеличить в 2 раза?
2.Приведите пример нулевой, конкурирующей
гипотезы.
3.Что представляют собой ошибки 1-го и 2-го рода?
4.Дайте определения свойствам эффективности, состоятельности и несмещенности оценок.
Задачи для самостоятельного решения
1.Ваш друг утверждает, что он умеет различать на вкус два близких сорта вина если и не всегда, то хотя бы в четырех случаях из пяти. Вы же склонны считать, что он просто угадывает.
2.Сформулируйте оба этих мнения в виде статистических гипотез и предложите какую-либо процедуру проверки. В чем состоят ошибки первого и второго рода?
3.Урна содержит большое количество белых и черных шаров, 100 раз производится следующее действие: из урны
206
наугад достается шар, фиксируется его цвет, затем шар опускается обратно в урну, после чего шары перемешиваются. Оказалось, что 67 раз достали белый шар. 33 раза - черный. Можно ли на 5%-м уровне значимости принять гипотезу о том, что доля белых шаров в урне составляет 0,6?
4. Обычно применяемое лекарство снимает послеоперационные боли у 80% пациентов. Новое лекарство, применяемое для тех же целей, помогло 90 пациентам из первых 100 оперированных. Можно ли на уровне значимости = 0,05 считать, что новое лекарство лучше? А на уровне = 0,01?
5.Игральный кубик бросили 60 раз, при этом числа 1, 2, 3, 4,5, 6 выпали соответственно 12, 9, 13, 11, 8, 7 раз. Можно ли на 5%- м уровне значимости отвергнуть гипотезу о симметричности кубика?
6.Трое рабочих работают на трех одинаковых станках. В
конце смены первый рабочий изготовил 60 деталей, второй - 80, третий -100 деталей. Можно ли на уровне значимости = 0,01 принять гипотезу о том, что производительности труда первых
двух |
рабочих равны между собой и в 2 раза меньше |
производительности третьего рабочего? |
|
7. |
Используя критерий Пирсона, при уровне значимости |
0.05 установить, случайно или значимо расхождение между эмпирическими частотами ni и теоретическими частотами ni' ,
которые вычислены, исходя из гипотезы о нормальном распределении генеральной совокупности Х:
ni |
5 |
10 |
20 |
8 |
7 |
ni' |
6 |
14 |
18 |
7 |
5 |
207
Лекция 14
Регрессивный анализ
В практике экономических исследований очень часто имеющие данные нельзя считать выборкой из многомерной нормальной совокупности. В этих случаях пытаются определить поверхность, которая дает наилучшее приближение к исходным данным. Соответствующие методы приближения получили название регрессивного анализа. В регрессивном анализе рассматривается односторонняя зависимость случайной зависимой переменной Y от одной (или нескольких) неслучайной независимой переменной X . Две случайные величины X и Y могут быть связаны либо функциональной зависимостью, либо статистической, либо быть независимыми.
При функциональной зависимости каждому значению переменной X соответствует вполне определенное значение переменной Y . Строгая функциональная зависимость реализуется редко, т.к. обычно величины подвержены еще действию различных случайных факторов. Тогда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Это статистическая (вероятностная, стохастическая) зависимость.
Корреляционной зависимостью между двумя случайными величинами, называется функциональная зависимость между значениями одной из них условным математическим ожиданием другой.
Рассмотрим двумерную случайную величину ( X ,Y ) , где X и Y - зависимые случайные величины. Представим величину Y - в виде линейной функции X :
Y g( X ) aX b ,
где a и b - параметры, подлежащие определению.
Это можно сделать различными методами, наиболее употребительный из них – метод наименьших квадратов.
208

Функцию |
g( X ) aX b |
называют |
наилучшим |
приближением Y в смысле метода наименьших квадратов, если математическое ожидание M [Y g( X )]2 принимает
наименьшее возможное значение.
Функцию g(x) называют линейной среднеквадратической регрессией Y на X .
|
Теорема Линейная среднеквадратическая регрессия Y на |
|||||||||||||
X имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g( X ) my |
y |
( X mx ) , |
|||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
||
|
M [ X ] , my M [Y ] , x |
|
|
|
|
|
||||||||
где mx |
|
D[ X ] , y D[Y ] , |
||||||||||||
-коэффициент корреляции величин Y и X . |
||||||||||||||
Коэффициент |
y |
|
- коэффициент регрессии Y на X , а |
|||||||||||
|
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|||
прямая называется прямой среднеквадратической регрессии Y |
||||||||||||||
на X . |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y m |
|
|
(x m |
) |
|
|
|
||||||
|
y |
|
|
|
|
|||||||||
|
|
|
|
|
x |
|
x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично можно получить прямую среднеквадратической регрессией X на Y :
x mx x ( y my ) .
y
Если коэффициент корреляции 1, то обе прямые
регрессии совпадают.
Для отыскания уравнений регрессии необходимо знать закон распределения двумерной случайной величины ( X ,Y ) .
На практике обычно располагают выборкой пар значений (xi , yi ) ограниченного объема. В этом случае речь может идти об оценке функции регрессии по выборке.
209

В качестве оценок условных математических ожиданий, принимают условные средние, которые находят по выборочным данным.
Условным средним Yx называют среднее арифметическое
наблюдавшихся |
значений |
Y , соответствующих |
X x . |
|||||||||||
Например, если |
при |
x1 2 |
величина |
Y приняла |
значения |
|||||||||
|
|
|
|
|
|
|
|
5 6 10 |
7 . |
|||||
y1 5, y2 6, y3 |
10 |
, то условное среднее Yx |
||||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|||
Уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* ( y) |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
Y |
g* (x) или X |
y |
|
|
|
||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|||
называются выборочными уравнениями регрессии, |
g* (x) и |
|||||||||||||
* ( y) - выборочными функциями регрессии, а их графики - выборочными линиями регрессии.
Метод наименьших квадратов для получения уравнения выборочной линии регрессии
Обычно для получения уравнения выборочной линии
регрессии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
b x b x2 |
... b xm |
||
|
Y |
|
|||||||
|
|
|
x |
0 |
1 |
2 |
|
m |
|
|
|
|
|
c |
c y c y2 |
... c ym |
|||
или |
X |
y |
|||||||
|
|
|
|
0 |
1 |
2 |
|
m |
|
используется метод наименьших квадратов.
Мы рассмотрим линейную регрессию, уравнение которой
Y b0 b1x.
Неизвестные параметры b0 и b1 выбираются таким образом,
чтобы
.
S( yi (b0 b1xi ))2 min
i 1n
210
