
Лекции по математике. Теория вероятности
.pdf
Показан полигон частот для ряда, представленного
ранее в примере.
Частота mx
50 |
|
|
|
40 |
|
|
|
30 |
|
|
|
20 |
|
|
|
10 |
|
|
|
0 |
|
|
|
2 |
3 |
4 |
5 |
|
|
Оценка х |
|
Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные
интервалы длиной h , а высотами – отрезки длиной ni 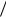 h (гистограмма частот) или wi
h (гистограмма частот) или wi 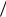 h (гистограмма относительных
h (гистограмма относительных
частот).
В первом случае площадь гистограммы равна объему выборки, во втором – единице
Определение Гистограмма – прямоугольники, с основаниями, равными интервалам значений признака и высотами, равными частотам.
Полигон (гистограмма) аналогичны кривой распределения, эмпирическая функция распределения – функции распределения случайной величины.
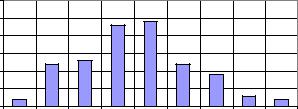
Гистограмма — это диаграмма, используемая, как правило, для представления интервального вариационного ряда.
Наиболее существенное отличие от полигона в том, что частота и относительная частота отображаются не точкой, а прямой, параллельной оси абсцисс на всем интервале.
Это объясняется тем, что данная частота (относительная частота) относится не к дискретному значению признака, а ко всему интервалу.
181
mh
30 |
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
30 |
42 |
54 |
66 |
78 |
90 |
102 |
114 |
126 |
|
|
|
|
aj |
|
|
|
|
Любой вариационный ряд можно изобразить графически в виде кривой накопленных частот — кумуляты. На оси абсцисс откладываются либо варианты, либо границы интервалов. На оси ординат — накопленная частота. Получают точки при пересечении каждой пары абсциссы и ординаты, которые соединяют плавной кривой.
Определение Кумулятивная кривая (кривая сумм) —
ломаная, составленная по последовательно суммированным, т.е. накопленным частотам или относительным частотам.
При построении кумулятивной кривой дискретного признака на ось абсцисс наносятся значения признака, а ординатами служат нарастающие итоги частот. Соединением вершин ординат прямыми линиями получают кумуляту.
При построении кумуляты интервального признака на ось абсцисс откладываются границы интервалов и верхним значениям присваивают накопленные частоты. Кумулятивную кривую называют полигоном накопленных частот.
Кумулятивная кривая строится для накопленных частот или накопленных относительных частот, причем по оси ординат откладывают верхнюю границу интервала соответствующего интервального ряда, так что последняя точка кумулятивной кривой всегда отвечает либо количеству наблюдений в выборке, либо единице.
182
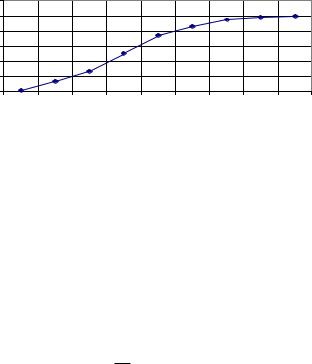
mhнак
120 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
30 |
42 |
54 |
66 |
78 |
90 |
102 |
114 |
126 |
|
|
|
|
aj |
|
|
|
|
По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X x . Кумулятивная кривая, то же, что график функции распределения.
Выборочная функция распределения
Определение Выборочной (эмпирической) функцией распределения называют функцию F x , определяющую для
каждого значения x относительную частоту события X x .
F * x nx n
,
где nx – число вариант, меньших x , n – объем выборки.
Замечание. В отличие от эмпирической функции распределения, найденной опытным путем, функцию
распределения F x генеральной совокупности называют
теоретической функцией распределения. F x определяет
вероятность события X x , а F x – его относительную
частоту.
Замечание При достаточно больших n , как следует из теоремы Бернулли, F x стремится по вероятности к F x .
183
Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F x , а именно:
1)0 F x 1.
2)F x – неубывающая функция.
3)Если х1 – наименьшая варианта, то F x 0 при x x1 ;
если xk – наибольшая варианта, то F x 1 при x xk .
Числовые характеристики вариационного ряда
К числовым характеристикам обычно относят так называемые средние (центральные) величины и меры, характеризующие разброс данных вокруг средних величин, а также некоторые другие дополнительные параметры, описывающие характер распределения опытных данных.
Средние величины — это характеристики, обобщенно представляющие одним числом всю выборку.
Существует несколько видов средних величин:
средняя арифметическая,
средняя геометрическая,
средняя гармоническая
Какой из них пользоваться в каждом конкретном случае определяется тем, какое свойство ряда желательно описать данной величиной.
Наиболее распространенной является средняя арифметическая или, как часто говорят, просто средняя.
Определение Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот.
m
xi ni
|
|
i 1 |
|
|
x |
|
, |
||
|
|
|||
|
|
|
n |
|
184
где xi - варианты дискретного ряда или середины интервалов вариационного ряда, ni - соответствующие им частоты,
m
n ni .
i 1
Это наиболее общая формула для вычисления средней арифметической.
Однако при большом числе наблюдений пользоваться ей не очень удобно, поэтому существуют некоторые другие более удобные формулы. В частности, если уже построены вариационные ряды, то среднюю арифметическую можно найти
с помощью частот по формулам: |
|
|
|
|
||||
x |
1 |
xmx |
и |
x |
1 |
xh mh |
||
n |
n |
|||||||
|
x |
|
|
h |
, |
|||
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
x x x |
и |
x xh h |
||||||
|
|
x |
|
|
|
|
h |
|
где x |
и xh |
— соответственно |
значение |
признака для |
||||
дискретного и интервального (центр интервала) ряда.
Для дискретного ряда эти формулы дают точные значения величин x , а для интервального ряда — приближенные, поскольку предполагают, что все значения наблюдаемой величины совпадают с центром интервала или равномерно распределены вокруг него.
Однако чем больше объем выборки, тем ближе приближенное значение к среднему.
Средняя арифметическая обладает рядом свойств, основными из которых являются следующие.
Свойства средней арифметической
1. Средняя арифметическая - это такая величина, которая обеспечивает неизменность суммы значений результатов наблюдений, если каждое из них заменить средней арифметической:
185

n |
n |
xi x nx |
|
i 1 |
i 1 |
2. Сумма отклонений результатов наблюдений от средней арифметической равна нулю:
n
( xi x) 0
i1
3.Средняя арифметическая сумм (разностей) двух рядов
наблюдении с одинаковым объемом выборок равна сумме (разности) средних арифметических этих рядов, если исследуемые признаки взаимно соответствуют друг другу:
( x y ) x y
Последнее свойство обобщается на любое количество рядов. Средняя арифметическая является важной характеристикой ряда наблюдений. Она показывает наиболее часто встречающееся, наиболее вероятное значение анализируемой величины и подобна математическому ожиданию в теории
вероятностей.
Но это не единственная средняя характеристика выборки. Часто в практике приходится прибегать к средней
геометрической, которая |
определяется |
как корень n - ой |
||||||
степени из произведения |
всех полученных измерений |
|||||||
(наблюдений): |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
x геом n |
x1 |
x2 xn |
|
xi |
|||
|
|
|
|
|
|
|
i 1 |
|
Часто употребляемыми характеристиками являются также мода и медиана.
Определение Медианой называется значение признака,
приходящееся на середину ранжированного ряда наблюдений. |
|
Медиана (Me или |
~ |
x ) - значение признака, для которого |
|
половина всех наблюдений меньше (соответственно половина больше) этого значения или, иначе говоря, срединное значение признака.
Наиболее просто медиану можно найти по графику кумулятивной кривой накопленных относительных частот,
186

определяя значение |
~ |
, отвечающее величине |
h = 0,5, или |
x |
ближайшего к нему целому для дискретного целочисленного ряда.
К вычислению медианы прибегают в том случае, когда надо определять значение признака, которое лежит в середине распределения.
Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов.
Пример |
|
|
|
|
|
|
||
n 50 |
|
- четное, |
серединных интервалов два |
|||||
x25 5, |
x26 |
5 |
x25 |
|
|
|
5 5 |
|
|
|
M |
x26 |
|
5 |
|||
|
|
|
2 |
|
2 |
|||
|
|
|
|
|
|
|
||
Для интервального вариационного ряда находится медианный интервал, на который приходится середина ряда, а значения медианы на этом интервале находят с помощью линейного интерполирования.
Определение Мода –вариант, которому соответствует наибольшая частота.
Мода (Мо) — это такое значение признака, которому отвечает максимум частоты или относительной частоты вариационного ряда. Для дискретного вариационного ряда значение моды определяется непосредственно из таблицы или по полигону частот (относительных частот).
Пример
Mo 5 , так как этому варианту соответствует наибольшая частота ni 22 .
Для интервального ряда сначала определяют модальный интервал, т. е. интервал, отвечающий наибольшей частоте признака. Обозначим через a0 начало модального интервала.
Через m |
( |
),m |
( |
) |
и m ( ) обозначим частоту |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
(относительная частота) модального, предшествующего и последующего интервалов. Тогда
187

Mo a0 |
h |
m m |
|||
|
0 |
0 |
|||
2m |
m |
m |
|||
|
|
||||
|
|
0 |
0 |
0 |
|
или |
|
|
|
|
|
Mo a0 |
h |
|
|||
|
0 |
0 |
|||
2 |
|
|
|||
|
|
||||
|
|
0 |
0 |
0 |
|
Обычно модой пользуются, чтобы установить, например, какая производительность труда, себестоимость продукции, объем ее выпуска и т. п. преобладают в данном ряду наблюдении, на данной группе предприятии, в данном районе, в данном году и т. п.
Определение Коэффициент ассиметрии – числовая характеристика вариационного ряда
|
|
|
m |
xi |
|
3 ni |
|
m3 |
|
|
x |
||
A |
|
i 1 |
|
|
|
|
s 3 |
|
n s 3 |
||||
|
|
|
||||
если A 0 , то распределение имеет симметричную форму,
т.е. варианты равноудалены от x , имеют одинаковую частоту. Ассиметрия характеризует симметричность распределения
относительно средней арифметической.
Определение Эксцесс - числовая характеристика вариационного ряда
|
|
|
m |
xi |
|
4 ni |
|
|
m4 |
|
|
x |
|
||
E |
3 |
i 1 |
|
|
|
3 |
|
s 4 |
|
n s 4 |
|||||
|
|
|
|
||||
Эксцесс или коэффициент эксцесса характеризуют остроту вершины полигона или гистограммы. Чем больше значение этих величин, тем острее вершина.
Эксцесс является показателем крутости вариационного ряда по сравнению с нормальным распределением. Если E 0 - то нормальное распределение.
188
Меры разброса опытных данных
Средние величины характеризуют всю выборку, при этом такие характеристики даются единственным числом. Степень изменчивости наблюдаемых значений или, как принято говорить, вариация признака такими характеристиками никак не учитывается. Однако на практике небезразлично, как разбросаны значения измеряемых величин.
Средняя арифметическая характеризует только центр рассеивания опытных данных. Нужны еще какие-то меры, которые характеризовали бы рассеяние этих данных вокруг центра. Таких мер существует несколько.
Простейшей из них является вариационный размах. Эта величина легко вычисляется, поэтому ею часто пользуются на практике. Однако эта характеристика, опираясь только на два крайних значения из всего ряда наблюдений, не учитывает, как расположены внутри этого интервала остальные значения.
Поэтому чаще используются более эффективные меры для оценки рассеивания.
Определение Дисперсия – средняя арифметическая квадратов отклонений вариантов от их средней арифметической
|
m |
xi |
|
2 ni |
|
|
|
x |
|||
s 2 |
i 1 |
|
, |
||
|
|
||||
|
|
n |
|||
где s - средне квадратическое отклонение.
Выборочная дисперсия является наиболее важной из них и равна
|
|
1 |
n |
|
в2 |
|
(xi x )2 - для неранжированного ряда |
||
|
||||
|
|
n i 1 |
||
Или |
|
|
|
|
в2 |
(xi x )2 h - для ранжированного ряда. |
|||
|
|
h |
||
Дисперсия полно характеризует меру рассеивания измеренных значений вокруг средней арифметической.
189

Чем меньше дисперсия, тем теснее группируются данные около центра рассеивания.
Дисперсия и средняя арифметическая имеют разные размерности, что создает затруднения при практических оценках. Поэтому часто прибегают к выборочному стандартному отклонению:
|
|
|
1 |
n |
|
в |
|
|
(xi x )2 |
- для неранжированного ряда или |
|
|
|
||||
|
|
|
n i 1 |
|
|
|
|
|
|
||
в |
|
(xi x )2 h |
- для ранжированного ряда. |
||
|
|
|
h |
|
|
Достаточно удобной величиной, дающей возможность оценить меру рассеивания, является выборочный коэффициент вариации, определяемый либо в относительных значениях, либо
в процентах: x |
x |
|
x |
||
|
Формулами, которыми значительно удобнее пользоваться на практике:
n
2 x2 x 2
в n i 1 i
2в xh h x 2
h1
Для подсчета истинных характеристик вводят поправки к группировке (поправки Шеппарда), при этом истинные моменты связываются
|
s |
2 s 2 |
|
1 |
|
h 2 , |
m3 m3 , |
|||||||
12 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
m |
|
m |
|
|
1 |
|
s 2 h 2 |
7 |
h 4 |
||||
4 |
4 |
2 |
240 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
A |
m3 |
, E E |
|
h k - ширина интервала |
||||||||||
s 3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
190
