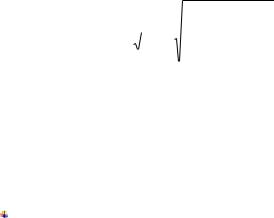
Замечание Т.е чем больше объем выборки, тем больше вероятность того, что ошибка оценки будет очень мала.
Убедимся, что среднее арифметическое значение x B представляет собой несмещенную оценку математического ожидания M x .
Будем рассматривать xB как случайную величину, а x1 , x2 , , xn , то есть значения исследуемой случайной
величины, составляющие выборку, |
– как |
независимые, |
одинаково распределенные случайные величины |
X1 , X 2 , , X n , |
имеющие математическое ожидание a . Из свойств математического ожидания следует, что:
|
|
|
|
|
|
|
|
|
|
X1 X X n |
|
|
|
|
|
|
M X B M |
|
|
|
a |
|
|
n |
|
|
|
|
|
|
|
Но, поскольку каждая из величин |
X1 , X 2 , , X n |
имеет такое |
же распределение, что и генеральная совокупность, |
a M X , |
то есть M X B M X , что и требовалось доказать.
Выборочное среднее является не только несмещенной, но и состоятельной оценкой математического ожидания.
Если предположить, что X1 , X 2 , , X n имеют ограниченные дисперсии, то из теоремы Чебышева следует, что их среднее
арифметическое, то есть X B , при увеличении n стремится по вероятности к математическому ожиданию каждой их величин,
то есть к M X .
Следовательно, выборочное среднее есть состоятельная оценка математического ожидания.
В отличие от выборочного среднего, выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности. Можно доказать, что
M DB n 1 Dr , n
где Dr – истинное значение дисперсии генеральной совокупности.


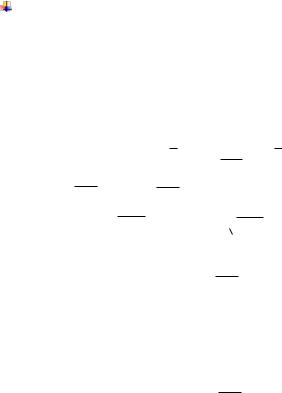





 0,25 0,5 ,
0,25 0,5 ,