Лекции по математике. Теория вероятности
.pdfM XY x1 y1 |
p1 g1 x2 y1 p2 g1 |
x1 y2 p1 g2 x2 y2 p2 g |
2 |
y1g1 |
x1 p1 x2 p2 y2 g2 |
x1 p1 x2 p2 |
|
y1 g1 y2 g2 x1 p1 x2 p2 M X M Y .
Замечание Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.
Дисперсия двумерных случайных величин
1) Дисперсия постоянной величины C равна нулю:
D C 0 .
Доказательство
D C M C M C 2 M C C 2 M 0 0 .
2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
D CX C 2 D X .
Доказательство
D CX M CX M CX 2
M CX CM CM X 2 .
M C 2 X M X 2 C 2 D X
3)Дисперсия суммы двух независимых случайных величин
равна сумме их дисперсий:
D X Y D X D Y .
Доказательство
D X Y M X 2 2XY Y 2 M X M Y 2
M X 2 2M X M Y M Y 2 M 2 X
.
2M X M Y M 2Y
M X 2 M 2 X M Y 2 M 2 Y D X D Y
131
Следствие Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.
Следствие Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.
4) Дисперсия разности двух независимых случайных
величин равна сумме их дисперсий: |
|
|
|
|
|
|||||||
|
|
|
|
D X Y |
D X D Y . |
|
|
|
||||
|
|
|
|
|
Доказательство |
|
|
|
||||
D X Y D X D Y D X 1 2 D Y D X D X |
||||||||||||
Плотности вероятности составляющих двумерной |
||||||||||||
случайной величины |
|
|
|
|
|
|
|
|||||
По определению плотности распределения |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dF(x, ) |
|
d |
|
f (x, y) |
|
|
|
f1 (x) |
dF1 |
(x) |
|
|
|
|
|
|
|
|
f (x, y)dy. |
|
dx |
|
dx |
|
dx |
|
|||||||
Аналогично находится
f 2 ( y) f (x, y)dx.
Условные законы распределения составляющих двумерной случайной величины
Рассмотрим дискретную двумерную случайную величину и найдем закон распределения составляющей X при условии, что
Y примет определенное значение (например,Y y1 .
Для этого воспользуемся формулой Бейеса, считая гипотезами события X x1, X x2 ,…, X xn , а событием А –
событиеY y1 .
При такой постановке задачи нам требуется найти условные вероятности гипотез при условии, что А произошло. Следовательно,
132
р(x |
|
/ y ) |
p(xi , y1 ) |
. |
i |
|
|||
|
1 |
p( y1 ) |
||
|
|
|
||
Таким же образом можно найти вероятности возможных значений Х при условии, что Y принимает любое другое свое возможное значение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р(xi / y j ) |
p(xi , y j ) |
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p( y j ) |
|
|
|
|
|
|
|
|
|
|
||||
Аналогично находят условные законы распределения |
|||||||||||||||||||||||||||||||||
составляющей Y: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p( y j / xi ) |
|
p(xi , y j ) |
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(xi ) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
Пример Найдем закон распределения Х при условии Y = |
|||||||||||||||||||||||||||||||
-0,8 и закон распределения Y при условии Х = 3 для случайной |
|||||||||||||||||||||||||||||||||
величины, рассмотренной в примере 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
р(x |
/ y ) |
0,1 |
|
1 |
|
0,2; |
|
|
|
|
р(x |
|
|
/ y ) |
0,3 |
|
3 |
0,6; |
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||
|
|
1 |
1 |
|
|
0,5 |
|
|
5 |
|
|
|
|
|
|
|
|
1 |
0,5 |
5 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
р(x |
|
/ y ) |
0,1 |
|
|
|
1 |
|
0,2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
0,5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
р( у |
/ х |
|
) |
|
0,3 |
|
|
6 |
; р( у |
|
|
/ х |
|
) |
0,25 |
|
5 |
. |
|
|
|
|||||||||||
|
|
1 |
|
2 |
|
|
0,55 |
|
|
11 |
2 |
|
|
2 |
|
0,55 |
11 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Определение |
|
|
Условной |
|
плотностью |
|
|
φ(х/у) |
||||||||||||||||||||||||
распределения |
|
составляющих |
|
|
X при |
|
|
|
|
данном |
значении |
||||||||||||||||||||||
Y y называется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(х / у) |
|
f (x, y) |
|
|
|
f (x, y) |
. |
|
|
|
|
|
|||||
|
|
f 2 ( y) |
|
|
||||
|
|
|
f (x, y)dx |
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
Аналогично определяется условная плотность вероятностиY |
||||||||
при X x : |
|
|
|
|
||||
( у / х) |
f (x, y) |
|
|
f (x, y) |
|
|||
|
|
|
||||||
f1 |
(х) |
f (x, y)dу |
|
|
133
Определение Начальным моментом порядка k , s
двумерной случайной величины ( X ,Y ) называется математическое ожидание произведения X k на Y s :
k ,s M ( X kY s )
Для дискретных случайных величин
k ,s xik ysj pij, i j
для непрерывных случайных величин
k ,s xk ys f (x, y)dxdy.
Определение Центральный момент порядка k, s
двумерной случайной величины ( X ,Y ) математическое ожидание произведения ( X M ( X ))k на (Y M (Y ))s :
k ,s M ((X M ( X ))k (Y M (Y ))s ).
Для дискретных случайных величин
k ,s (xi M ( X ))k ( y j M (Y ))s pij, i j
для непрерывных случайных величин
k ,s (x M ( X ))k ( y M (Y ))s f (x, y)dxdy.
При этом M ( X ) 1,0 ,
M (Y ) 0,1 , D( X ) 2,0 , D(Y ) 0,2 .
Корреляционный момент системы двух случайных величин
Определение Ковариация или корреляционный момент
K xy случайных величин ( X ,Y ) называется математическое ожидание произведения отклонений этих величин от своих
математических ожиданий.
K xy M X M x Y M y
134
Для дискретных случайных величин корреляционный момент находим
n |
m |
y j a j |
pij |
K xy xi ax |
|||
i 1 |
j 1 |
|
|
для непрерывных случайных величин
Кху (x M ( X ))(y M (Y )) f (x, y)dxdy.
Корреляционный момент описывает связь между составляющими двумерной случайной величины.
Действительно, |
убедимся, что для независимых X и Y |
||
K xy 0. |
|
|
|
В этом случае f (x, y) f1 (x) f2 ( y), |
тогда |
||
|
|
|
|
K xy (x M ( X )) f1 (x)dx ( y M (Y )) f2 ( y)dy 1 (x) 2 ( y) 0. |
|||
|
|
|
|
Итак, две независимые случайные величины являются и |
|||
некоррелированными. |
|
||
|
Замечание |
Корреляционный |
момент системы двух |
случайных величин - второй смешанный центральный момент: Ковариация (от англ. covariation - "совместная вариация") -
мера линейной зависимости двух величин. Ковариация показывает, есть ли линейная взаимосвязь между двумя
случайными величинами, |
|
|
|
Определение |
Коэффициент |
корреляции |
- |
безразмерный коэффициент коррелированности двух случайных величин
q |
Kxy |
. |
|
x y |
|||
|
|
Коэффициент корреляции показывает характер изменения двух случайных величин.
Однако, понятия коррелированности и зависимости не эквивалентны, а именно, величины могут быть зависимыми, но при этом некоррелированными.
135
Дело в том, что коэффициент корреляции характеризует не всякую зависимость, а только линейную.
В частности, если Y aX b, то q 1 .
Формула для коэффициента корреляции была введена Фрэнсисом Гальтоном
Фрэнсис Гальтон (1822-1911) — английский исследователь, внес вклад во многих областях науки:
метеорология (антициклон и первые общедоступные погодные карты),
статистику (регресс и корреляция)
криминологию (отпечатки пальцев). Математически обосновал практическую невозможность совпадения отпечатков пальцев у людей
Найдем возможные значения коэффициента корреляции.
Теорема |
Коэффициент корреляции |
| q | 1. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
Доказательство |
|
|
|||||||
Докажем сначала, что | K xy | x y . |
|
|
||||||||||||||||
Действительно, |
|
если рассмотреть случайную величину |
||||||||||||||||
Z1 y X xY |
|
|
|
и |
|
|
|
|
|
найти |
|
ее |
дисперсию, |
то |
||||
получим: D(Z ) 2 |
2 2 |
2 |
K |
xy |
. |
|
|
|||||||||||
|
1 |
|
|
|
x y |
|
|
|
|
x y |
|
|
|
|
||||
Так как дисперсия всегда неотрицательна, то |
|
|||||||||||||||||
2 2 2 |
2 |
y |
K |
xy |
0, |
|
|
|
|
|
||||||||
x y |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда |
|
| K xy | x y . |
|
|
|
|
|
|||||||||||
Отсюда |
|
|
Kxy |
|
|
|
|
|
q |
|
0, что и требовалось доказать. |
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
x y |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение Случайные величины называются некоррелироваными, если их коэффициент корреляции равен
нулю
q 0
Таким образом из независимости случайных величин следует их некоррелированность. Обратно не верно
136
Свойства ковариации и коэффициента корреляции
1.Ковариация двух случайных величин характеризует степень зависимости случайных величин.
2.Ковариация двух независимых случайных величин равна
нулю.
3.Корреляционный момент
K xy M ( XY ) M ( X ) M (Y )
4.Ковариация по абсолютной величине не превосходит их средних квадратических отклонений.
5.Коэффициент корреляции отношение их ковариации к произведению средних квадратических отклонений
6.Коэффициент корреляции 1 q 1
7. Коэффициент корреляции q 0 равен нулю, если сл.величины независимы.
8. Если q 1 , то между сл.величинами существует
линейная функциональная зависимость.
Замечание Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод о их независимости.
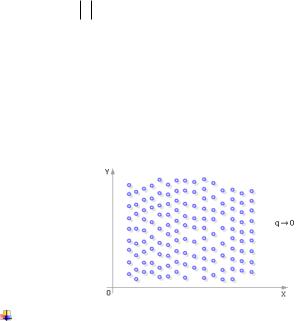
Пример Коэффициент корреляции стремится к нулю, любому значению X может соответствовать любое значение Y , то есть события X и Y не зависят или почти не зависят друг от друга, не коррелируют друг с другом
Пример При q близких к единице одному значению X
могут соответствовать уже несколько значений Y , события X и Y менее коррелированы, менее зависимы друг от друга
137
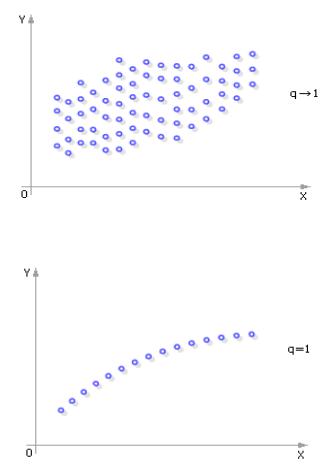
Пример Если q 1 коэффициент корреляции, то зависимость событий X и Y взаимно однозначная.
Пример Вид зависимости двух случайных величин при отрицательном коэффициенте корреляции
a) q 1 ; б) 1 q 0 ; в) q 0
138
Определение Корреляционная матрица системы двух
случайных величин X и Y - матрица вида
D |
q |
K |
|
q |
D |
Пример Распределение |
вероятностей случайной |
величины задано таблицей |
|
Определить математические ожидания случайных величин
X ,Y .
Решение
3 |
3 |
|
|
|
M X xi |
pij |
1(0,1 0,2 |
0) 0(0,3 0 0,1) 1(0,1 0 0,2) 0 |
|
i 1 |
j 1 |
|
|
|
3 |
3 |
|
|
|
M Y yi |
pij |
0(0,1 0,3 |
0,1) 1(0,2 0 0) 2(0 0,1 0,2) 0,8 |
|
i 1 |
j 1 |
|
|
|
Пример Задана плотность распределения системы случайных величин X и Y .
139
f (x, y) |
|
1 |
|
|
|
||
2 (x2 |
y2 x2 y2 1) |
||
|
Выяснить являются ли независимыми случайные величины
X и Y . |
|
|
|
|
|
|
|
|
|
Для |
решения этой задачи преобразуем плотность |
||||||||
распределения: |
|
|
|
|
|
|
|
||
|
1 |
|
1 |
|
1 |
1 |
|
||
f (x, y) |
|
|
|
|
|
|
|
|
|
2 (1 x2 y2 (1 x2 )) |
2 (1 x2 )(1 y2 ) |
(1 x2 ) (1 y2 ) |
|||||||
Плотность распределения - произведение двух функций, Т.е. случайные величины X и Y независимы, они также будут и некоррелированы
В отличие от коэффициента корреляции, который меняется от -1 до 1, ковариация не инвариантна относительно масштаба, т.е. зависит единицы измерения и масштаба случайных величин.
Случайные величины могут быть зависимыми в то время как их ковариация нулевая!
Замечание Знак ковариации указывает на вид линейной связи между рассматриваемыми величинами: если ковариация0 - это означает прямую связь (при росте одной величины растет и другая), ковариация 0 указывает на обратную связь. При ковариации 0 линейная связь между переменными отсутствует.
Пример По данным корреляционной таблицы найти выборочный корреляционный момент (ковариацию):
|
X |
-1 |
0 |
1 |
2 |
Y |
|
||||
|
|
|
|
|
|
2 |
|
20 |
10 |
0 |
30 |
|
|
|
|
|
|
3 |
|
0 |
10 |
20 |
10 |
|
|
|
|
|
|
Решение
Выборочный корреляционный момент xy определяется равенством:
xy 1n nxy xy x y .
140