Лекции по математике. Теория вероятности

Линейный регрессионный анализ

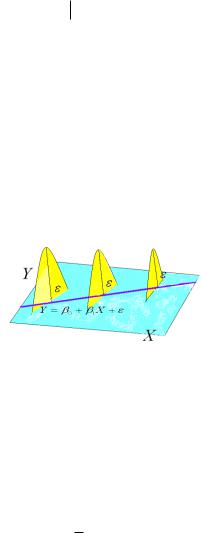
Термином линейный регрессионный анализ обозначают прогнозирование одной переменной на основании другой, когда между этими переменными существует линейная взаимосвязь

Y b0 b1 X .

Разности между фактически полученными значениями Y и вычисленными по уравнению регрессии соответствующими

значениями прогнозов Y называются отклонениями e Y Y . Величины прогноза являются моделируемыми значениями данных, а отклонения показывают отличия от модели.

Пример Анализ зависимости между ценами и объемам продаж молока фермера. Значение выборочного коэффициента корреляции r 0.86 . Уравнение регрессии

Задачами регрессионного анализа являются:

установление формы зависимости между переменными;

оценка функции регрессии;

оценка неизвестных значений (прогноз значений) зависимой переменной.

В регрессионном анализе рассматривается односторонняя зависимость случайной зависимой переменной Y от одной (или

нескольких) независимой переменной X .

также называется функцией отклика, выходной, результирующей, эндогенной переменной; X - входной, объясняющей, предсказывающей, предикторной, экзогенной переменной, фактором, регрессором.

212

Линейная зависимость может быть представлена в виде модельного уравнения регрессии

M [Y X ] 0 1 x .

В силу воздействия неучтенных случайных факторов отдельные наблюдения y будут в большей или меньшей

степени отклоняться от функции регрессии

g(x) 0 1x.

В этом случае уравнение взаимосвязи двух переменных (парная регрессионная модель) может быть представлено в виде

Неизвестными параметрами являются 0 , 1 и 2.

определяется с помощью остаточной дисперсии 2 .

Оценкой дисперсии является выборочная остаточная дисперсия s 2 :

213

оценки и демонстрирует величину отклонения точек исходных данных от прямой регрессии.

Поскольку, как правило, требуется, чтобы прогноз был как можно более точным, значение s должно быть как можно меньшим.

Пример Для данных продажи молока s 2.72. Для величины Y , принимающей значения от 3 до18, значение s довольно велико.

Чтобы получить точечный прогноз, или предсказание для данного значения X , надо просто вычислить значение функции регрессии в точке X .

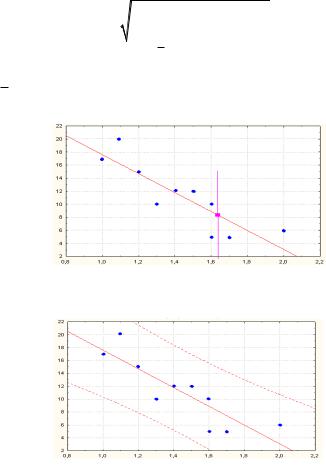
Пример Фермер хочет получить прогноз количества молока, которое будет продано при цене 1.63 рублей за литр:

Y 32.14 14.54X

Y 32.14 14.54 1.63 8.44

Конечно, реальные значения величины Y не лежат в

точности на регрессионной прямой. Есть два источника неопределенности в точечном прогнозе, использующем уравнение регрессии.

214

1.Неопределенность, обусловленная отклонением точек данных от выборочной прямой регрессии.

2.Неопределенность, обусловленная отклонением выборочной прямой регрессии от регрессионной прямой генеральной совокупности.

Интервальный прогноз значений переменной можно построить так, что при этом будут учтены оба источника неопределенности.

Суммарная дисперсия

sY s2 sY2 ,

где sY - стандартная ошибка прогноза, s - стандартная ошибка оценки, sY - стандартная ошибка функции регрессии.

Величина sY2 измеряет отклонение выборочной прямой

регрессии от регрессионной прямой генеральной совокупности и вычисляется для каждого значения X как.

распределение Стьюдента с k n 2 степенями свободы.

215

Пример Найдем стандартную ошибку прогноза в точке X 1.63 с надежностью 0.95 .

При X 1.63 значение Y 8.44 . Находим интервал прогноза

Y t sY 8.44 2.306 2.91 8.44 6.71

или 1.73 Y 15.5

Построенные аналогичным образом интервалы значений прогноза по всем значениям X имеют вид:

Интервал прогноза очень велик, это связано с тем, что исходная выборка мала, а значение s сравнительно велико.

216

Прогноз значений зависимой переменной по уравнению регрессии оправдан, если значение объясняющей переменной не выходит за диапазон ее значений по выборке (причем тем более точный, чем ближе X к X ).

Экстраполяция кривой регрессии, т.е. использование вне пределов обследованного диапазона значений объясняющей переменной может привести к значительным погрешностям.

Проблемы применения метода линейной регрессии

1. Если истинная взаимосвязь не линейная, нельзя использовать для прогноза прямую линию. Большинство компьютерных программ не предупреждают об этом.

2. Экстраполяция за пределы имеющихся данных потенциально опасна. Вы не располагаете информацией, чтобы отбросить другие возможности.

217

3.Резко отклоняющееся значение может серьезно повлиять на результаты регрессионного анализа.

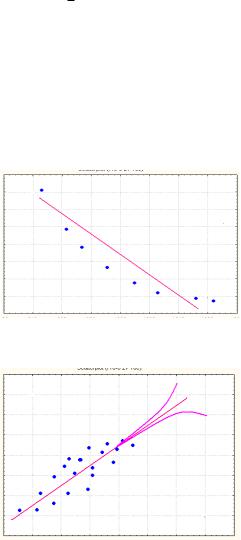
4. Большое значение имеет то, какая из двух переменных прогнозируется, а какая служит основанием для прогноза. Каждому из этих подходов соответствует своя линия регрессии. Две линии регрессии сближаются, когда уменьшается фактор случайности точки данных приближаются к прямой линии.

Основные предпосылки статистической модели линейной регрессии

Y 0 1 X

относительно регрессионной прямой совокупности.

218

На практике приемлемые результаты получаются и тогда, когда значения Y имеют нормальное распределение лишь приблизительно.

3. Разброс генеральной совокупности данных относительно регрессионной прямой совокупности остается постоянным всюду вдоль этой прямой (дисперсия зависимой переменной Y остается постоянной: D[Y ] 2 ).

4 Возмущения , а, следовательно? и значения Y независимы между собой.

Уравнение взаимосвязи двух переменных (парная регрессивная модель) может быть представлена

y x

где - случайная переменная, характеризующая отклонение от функции регрессии. - называют возмущением.

Рассмотрим линейный регрессивный анализ, для которого

функция x линейна M (Y ) 0 1 X

Если для оценки параметров линейной функции взята выборка, то парная линейная регрессионная модель имеет вид

Yi 0 1 X

Задачи регрессионного анализа

Цель регрессионного анализа состоит в определении общего вида уравнения регрессии, построении статистических оценок неизвестных параметров, входящих в уравнение регрессии и проверке статистических гипотез о регрессии.

Корреляционный анализ позволяет устанавливать неслучайность (значимость) изменения наблюдений Yi и

степень их зависимости от случайных величин X . Регрессионный анализ представляет собой следующий этап

статистического анализа.

219

Определяются точные количественные характеристики изменения Y . Статистическая связь Y и X сводится к строгим (неслучайным) соотношениям.

( 1 ,..... n )

анализ точности полученного уравнения регрессии, связанный с построением доверительных интервалов для

X( X 1 ,.......X n ) .

1.Возмущения есть случайная величина, а объясняющая переменная – неслучайная величина.

2. Математическое ожидание возмущения равно нулю

M ( i ) 0

3. Дисперсия возмущения постоянна для любого i :

D( i ) 2

4. Возмущения не коррелированны (независимы)

M ( i j ) 0 ; i j

5. Возмущения есть нормально распределенная случайная величина.

Для получения уравнений регрессий достаточно 1-4 условий, 5 условие для оценки точности уравнений регрессии и его параметров

Пусть требуется исследовать зависимость Y ( X ) , величины

Xи Y измеряются в одном эксперименте.

Восстановим Y ( X ) по результатам измерений. Точное

представление Y ( X ) невозможно. Будем искать приближенную зависимость по методу наименьших квадратов. Y ( X ) g(x) ,

220