§14.3. Связь между векторным полем напряжённости и скалярным полем потенциала

Очевидно, что распределение в пространстве потенциала данного электростатического поля с точки зрения математики представляет скалярное поле . Оказывается, последняя формула предыдущего параграфа указывает на то, чтовекторное поле напряжённости однозначно определяется заданием скалярного поля потенциала. Значит, данное электростатическое поле одинаково успешно может быть представлено как векторным полем , так и скалярным полем. Покажем это.

Используя координатное представление скалярного произведения в декартовых координатах, перепишем выражение элементарного изменения потенциала:

.

С другой стороны, поскольку , то дифференциал в соответствие с правилами дифференцирования функции многих переменных

.

Сравнивая эти два равенства, приходим к выводу, что

Значит, действительно, задание скалярного поля определяет все его частные производные, а это, оказывается, определяет проекции векторана координатные оси, что, очевидно, однозначно определяет вектор. Таким образом,поле напряжённости получается в результате процедуры трехмерного дифференцирования поля потенциала. Эта математическая процедура называется градиентом.

В математике процедуру или совокупность действий по преобразованию функции называют оператором. Градиент является многомерным дифференциальным оператором. В трёхмерном случае (случай функции 3-х переменных) градиент обозначается и выражается так:

.

Есть ещё одно более краткое обозначение, подчёркивающее векторный характер оператора. Это символ , называемый вектором набла. С его помощью операция взятия градиента скалярного поля обозначается как произведение вектора набла на скаляр: .

Итак, мы можем записать:

.

Из собственного опыта мы знем, что физический смысл градиента достаточно труден для понимания. Поэтому нелишне будет воспроизвести здесь страницу из учебника математики и обсудить её.

Выберем в пространстве, натянутом на декартовы координаты, произвольное направление, задаваемое ортом , и введём координату по этому направлениюL (рис.14.3).

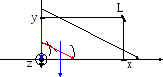Рис.14.3

Если мы не будем сходить с оси L, то скалярная функция положения будет зависеть только от координаты L:

Из рисунка легко сообразить, что

Аналогично:

; .

Теперь найдем производную трёхмерной скалярной функции по направлению, то есть. По правилу дифференцирования сложной функции

.

Но проекция орта на направлениеопределяется так:, то есть

Тогда производная по направлению принимает вид:

Итак, пространственная быстрота изменения скалярной функции от положения в направленииравна скалярному произведению градиента на орт направления. Значит, есть такие направления, вдоль по которым  в данной точке пространства не меняется, то есть =0, следовательно,

.

Совокупность таких направлений в данной точке пространства образует поверхность

Рис.14.4

С другой стороны, направление (рис.14.4) будет параллельно градиенту, следовательно, вдоль по этому направлению быстрота пространственного изменения функции  будет максимальна и её абсолютная величина будет, как раз, равна модулю градиента. Отсюда «понятное» определение: градиент функции от пространства  в данной точке − это вектор максимальной пространственной быстроты изменения функции в этой точке. Тогда для напряжённости электростатического поля можно дать такое утверждение: вектор в данной точке пространства есть вектор максимальной пространственной скорости убывания потенциала в этой точке. Отсюда, кстати, проистекает наиболее часто применяемая размерность напряжённости: .

Как следует из сказанного, поверхность в данной точке пространства - это поверхность, вдоль по которой потенциал не изменяется. Такая поверхность называетсяэквипотенциальной. Картина силовых линий − не единственный способ представления потенциального поля. Его можно представить совокупностью эквипотенциальных поверхностей, соответствующих значениям потенциала, отстоящих друг от друга на одинаковый (произвольно выбранный) сдвиг :

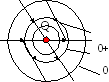Рис.14.5

₀+2

Левый рисунок соответствует однородному полю, а правый − центральному полю точечного источника.