Глава 13. Электростатика. Теорема остроградского-гаусса для напряжённости электростатического поля в вакууме

§13.1. Вектор площади

В механике обсуждалась векторная природа площади, и вводился вектор площади плоской поверхности

,

где − орт нормали к поверхности.

Рис.13.1

В случае, если поверхность не плоская, речь всегда идёт о векторе элементарной поверхности

.

Тогда орт − нормаль к касательной плоскости в точке нахождения элементарной поверхности.

Понятно, что нормаль к плоскости можно провести в двух противоположных направлениях. Выбор правильного направления может быть связан с разными критериями. В механике использовался критерий направления обхода площади по периметру. В данной теме мы будем иметь дело только с замкнутыми поверхностями. Правильный выбор орта нормали такой, чтобы он был обращён вовне замкнутой поверхности:

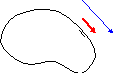Рис.13.2

С векторами площадей можно производить все векторные операции, в том числе их можно скалярно умножать друг на друга и проецировать на определённое направление. Рассмотрим большую поверхность, направление которой определяется нормалью , и поверхность поменьше, вектор которой обозначим. По правилам векторной алгебры проекция векторана направлениеравно скалярному произведению

.

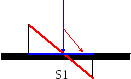Рис.13.3

Геометрический смысл этой операции показан на рисунке 13.3. Площадь S₁ является участком исходной большой поверхности, каждая точка которого представляет собой пересечение этой поверхности с перпендикуляром, опущенным на неё из соответствующей точки S₂.

§13.2. Телесный угол

Рассмотрим элементарную поверхность dS_сф, принадлежащую сфере с центром в точке О радиуса r. По определению телесным углом d, под которым видна часть поверхности сферы dS_сф из центра сферы, называется отношение площади dS_сф к квадрату радиуса сферы:

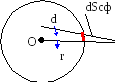Рис.13.4

Это безразмерная величина, которая является характеристикой совокупности направлений, выходящих из точки О и пересекающих элемент поверхности dS_сф и его периметр.

d численно равен элементу поверхности сферы единичного радиуса, пересекаемого теми же направлениями. Полный телесный угол  равен полной поверхности сферы единичного радиуса, то есть 4.

Рассмотрим (рис.13.5) элементарную поверхность , находящуюся в той же точке пространства, что и поверхность сферырадиусаr, и видимую под тем же телесным углом d из точки О:

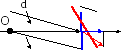Рис.13.5

Очевидно, что орт нормали к поверхности dS_сф (обозначим его ) можно определить так:

.

Из-за малости угла d все радиальные линии, пересекающие dS_сф и dS считаются параллельными вектору и, следовательно, перпендикулярнымиdS_сф. Это означает, что величина dS_сф представляет собой проекцию вектора на направление радиального орта, то есть

,

следовательно,

§13.3. Поток вектора через поверхность

Пусть точке пространства, в которой находится элементарная поверхность , соответствует вектор поля. Тогда по определению можно ввести понятиеэлементарного потока векторного поля через поверхность:

Интеграл элементарных потоков по поверхности S, погружённой в векторное поле , по определению называется потоком вектора через поверхностьS: