§13.4. Теорема ог

Если − напряжённость поля точечного зарядаQ, то в точке пространства, отстоящей от источника на вектор ,

,

где . Тогда элементарный поток через поверхность, находящуюся в этой точке и направленнуюот заряда, имеет вид:

.

Понятно, что d − телесный угол, под которым видна поверхность из точки расположения источника. Отметим, что выражение потока напряжённости через телесный угол оказалось возможнымисключительно благодаря обратной квадратичной зависимости напряжённости поля точечного источника от расстояния.

Подсчёт потока напряжённости поля точечного заряда через замкнутую поверхность S рассмотрим в двух случаях.

а) Заряд находится внутри поверхности S

Рис.13.6

Из рисунка 13.6 видно, что интегрирование в этом случае производится по полному телесному углу.

б) Заряд находится вне поверхности S

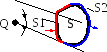Рис.13.7

Под телесным углом  (рис.13.7) из точки Q видны две поверхности, образующие замкнутую поверхность S: S₁, нормали которой обращены к заряду, и S₂, нормали которой обращены от него.

.

Теперь в первом интеграле интегрирование производится по поверхности, нормали которой тоже обращены от источника, следовательно, теперь оба слагаемых могут быть выражены через телесный угол :

;

Тогда понятно, что полный поток через поверхность S равен 0.

Если имеется совокупность точечных зарядов, то в соответствии с принципом суперпозиции полей

,

где N − количество точечных источников. Следовательно, поток напряжённости их общего поля через произвольную замкнутую поверхность S:

,

где _i=1, если Q_i находится внутри замкнутой поверхности и _i=0, если Q_i находится за пределами замкнутой поверхности, следовательно, − заряд, охваченный замкнутой поверхностью. Тогда окончательно:

Поток напряжённости электрического поля через произвольную замкнутую поверхность в вакууме равен заряду, охватываемому этой поверхностью, делённому на электрическую постоянную вакуума.

§13.5. Применение теоремы ог

Теорема даёт возможность рассчитать электрическую напряжённость поля распределённого заряда в случаях простых, но важных пространственных конфигураций.

13.5.1. Напряжённость поля равномерно заряженной сферы

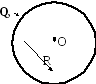Рис.13.8

Равномерность заряда сферы означает, что её поверхностная плотность заряда одинакова во всех точках сферы:

,

где R − радиус сферы, а Q − её заряд (для простоты будем считать, что он положителен).

Сначала рассмотрим произвольную точку А внутри сферы заряда.

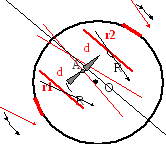Рис.13.9

Рассмотрим два вертикальных малых телесных угла d, под которыми из точки А видно два участка поверхности сферы заряда dS₁ и dS₂ (рис.13.9). Из рассмотренной выше связи площади и телесного угла, под которым она видна, следует:

С каждой из этих элементарных поверхностей связан элементарный заряд

соответственно. Силы, действующие со стороны этих зарядов на пробный заряд q>0, помещённый в точку А (рис.13.10), в соответствие с законом Кулона равны по модулю:

и противоположны по направлению.

Рис.13.10

Следовательно, полная сила, действующая со стороны поверхности сферы заряда на пробный заряд q и связанная с интегрированием по полному телесному углу, будет равна 0. А поскольку, , то из равенства 0 силы следует равенство 0 напряжённости в любой точке внутри сферы.

Теперь рассмотрим сферическую поверхность S, концентрическую сфере заряда, радиус которой .

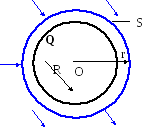Рис.13.11

Очевидно, что система (заряд и его поле) обладает сферической симметрией относительно точки О . Отсюда можно сделать два вывода: во-первых, любой физический вектор, характеризующий данную систему, должен быть направлен по радиальной относительно точки О линии; во-вторых, все точки любой сферы, концентрической сфере заряда должны быть физически эквивалентны друг другу. Следовательно, векторы на поверхностиS будут направлены радиально, то есть перпендикулярно поверхности, а модули их будут одинаковы.

Поток напряжённости через S по определению:

,

Последнее равенство выполняется, так как векторы оба направлены радиально от центра, то есть параллельны друг другу. Поскольку модульЕ одинаков на сфере S, его можно вынести за знак интеграла:

.

Поверхность, поток вектора поля через которую равен произведению постоянного модуля на площадь поверхности, называется гауссовой по отношению к данному векторному полю. Как видно, в рассматриваемом случае все сферы, концентрические сфере заряда, являются гауссовыми. Возможность найти гауссову поверхность объединяет все системы, которые будут рассматриваться в этом параграфе.

По теореме ОГ

.

Тогда мы имеем равенство:

,

следовательно,

.

Теперь сформулируем вывод:

на поверхности и за пределами равномерно заряженной сферы электростатическое поле ничем не отличается от поля точечного заряда, помещённого в центр сферы и равного заряду сферы; внутри сферы напряжённость равна 0.

13.5.2. Напряжённость поля равномерно заряженной бесконечной плоскости

Очевидно, что система обладает плоской зеркальной симметрией относительно плоскости заряда. Полупространства слева и справа от этой плоскости являются зеркальным отражением друг друга в ней (поверхность на рис.13.12 изображена «в ребро»).

Рис.13.12

А любые полупространства «верх-низ» физически эквивалентны друг другу. Значит, не существует ни одного вектора, характеризующего систему, который мог быть направлен снизу вверх или сверху вниз. Это же относится к направлениям «на нас − от нас». Следовательно, напряжённость поля плоскости должна быть направлена перпендикулярно плоскости, кроме этого, она не должна изменяться в направлениях вдоль плоскости. Она также не имеет права изменяться в направлении перпендикулярно плоскости в пределах одного (левого или правого полупространства). Это следует из бесконечности плоскости заряда, поскольку как бы далеко мы от неё не отошли, мы по-прежнему находимся рядом с ней.

Гауссовой поверхностью S для этой системы является «консервная баночка», боковая поверхность которой перпендикулярна плоскости заряда, а основания ей параллельны.

Поток напряженности через S по определению

.

Последний интеграл равен 0, поскольку на боковой поверхности и их скалярное произведение равно 0. В силу зеркальной симметрии, параллельности векторовна основаниях и неизменности векторавдоль по основаниям

.

Значит,

.

По теореме ОГ

.

Легко сообразить, что заряд, охваченный «консервной баночкой» гауссовой поверхности S, сосредоточен на площади S_осн, вырезаемой ею на плоскости заряда. Следовательно, . Значит, по теореме ОГ имеем:

.

Тогда можно составить равенство:

.

Проведя сокращение, получаем:

13.5.3. Напряжённость поля равномерно заряженной бесконечной прямой нити

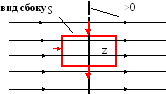
Рис.13.13

вид сверху

Рисунки 13.13 отражают цилиндрическую симметрию системы. Гауссовой поверхностью S для этой системы является также «консервная баночка» в виде цилиндра, коаксиального заряженной нити. Её боковая поверхность параллельна оси заряда, а основания ей перпендикулярны.

Из рисунка видно, что на основаниях поток равен 0, а на боковой поверхности

.

Поток напряжённости по тереме ОГ:

.

Тогда получаем равенство:

.

После сокращения получаем:

Контрольные вопросы к главе 13

1. Чему равна сила взаимодействия двух скрещивающихся под прямым углом равномерно заряженных нитей с линейными плотностями соответственно равными 1 нКл/м и -0,5 нКл/м? (Ответ: 2,8 нН)

2. Две одинаковые квадратные тонкие плоские равномерно заряженные пластины расположены против друг друга параллельно друг другу. Площади пластин равны 100 см². Расстояние между пластинами равно 1,5 мм. Заряд одной пластины равен 50 нКл, другой  (150) нКл. Чему равна сила взаимодействия между пластинами? (Ответ: 424 мкН)

3. При значении напряжённости электрического поля, равном 310⁶ В/м воздух ионизуется и перестаёт быть изолятором. В результате, с заряженных тел, которые он окружает, может стекать заряд. Какой диаметр должен иметь равномерно заряженный провод с линейной плотностью заряда 2 мкКл/м, чтобы удержать заряд? (Ответ: 1,2 см)

4. В равномерно заряженном шаре с объёмной плотностью заряда, равной 5 нКл/м³ вырезали сферическую полость, центр которой находится на расстоянии 2 см от центра шара. Чему равна напряжённость поля внутри полости? (Ответ: 3,8 В/м)