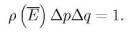
115 |
Молекулярная физика |
Можно показать: Плотность вероятности остается постоянной при движении системы по своей фазовой траектории.
Это очень важный результат. Можно сказать, что макроскопическая система совершает столь сложное движение, что "забывает"о своем начальном состоянии и "помнит"только о своей полной энергии. Все огромное количество переменных, от которых зависит функция распределения макроскопической подсистемы, свелось к ее зависимости от одной единственной величины – энергии:
ln ρ n { q, p} = α + β En { q, p} |
(2.2) |
Очень важно, что для всех подсистем, из которых состоит рассматриваемая система, параметры α и β одинаковы.
Ведем объем фазового пространства, где находится наша подсистема все время наблюдения.
Фазовый объем Dp q характеризует размеры той области фазового пространства, в которой равновесная подсистема может находиться с заметной вероятностью.
Рассмотрим, как связаны число состояний Γ в заданном интервале энергий |
и элемент |
||
фазового объема |
Ω . Или другими словами, сколько состояний |
Γ содержится в элементе |
|
фазового объема |
Ω . Для этого необходимо вспомнить один |
из главных |
принципов |
квантовой механики – принцип неопределенности. Принцип неопределенности утверждает, что координата и импульс любой частицы не могут быть определены одновременно со сколь угодно большой точностью. Неопределенности этих величин удовлетворяют неравенству:
pi qi ≥2 π h
где h - постоянная Планка.
Это выражение должно выполняться для всех N степеней свободы рассматриваемой системы.
Соответственно, D W ³ (2π h) N
Можно сказать, что величина (2π h) N равна минимальному объему ячейки в фазовом
пространстве. Тогда число состояний |
Γ |
в элементе фазового объема |
Ω равно (число |
|||||
«элементарных» ячеек в объеме |
Ω ): |
|
|
|
|
|
|
|
|
D |
G |
= |
|
Ω |
(3) |
||
|
( 2π h)3N |
|
||||||
Это и есть искомая связь между |
Ω и |
Γ . |
|
|
|
|
|
|
Т.е энтропия системы в классическом случае |
|
p q |
|
|||||
|
S |
= |
k ln |
(4) |
||||
|
(2π h)N |
|
||||||
116 |
Молекулярная физика |
7.3.Связь энтропии с функцией распределения. Классический случай
Ранее мы ввели объем фазового пространства, где находится наша подсистема все время наблюдения.
p |
q =1/ ρ(`E) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S = |
k ln |
p q |
= ln |
|
1 |
|
|
= |
− k ln((2π h)N ρ ( |
|
)) |
|||||
|
|
|
E |
|||||||||||||
|
|
|
|
|
|
|
||||||||||
(2π h)N |
(2π h)N ρ (E ) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
С учетом того, что ln ρ |
|
|
} = α |
+ |
|
|
|
|||||||||
{ E |
β E = < ln ρ { E} > , получаем, |
|||||||||||||||
S =−k <(2 π h)3 N lnρ(E )>=−k∫ρ( E( p ,q))[lnρ(E ( p ,q))]d Ω
В последней формуле мы воспользовались определением средних для любых физических величин:
Термодинамически неравновесные состояния
При термодинамическом определении энтропии мы встретились с трудностью распространения этого понятия на случай термодинамически неравновесных состояний. Формула Больцмана ((5) на стр.102) дает принципиальный способ преодоления указанной на трудности. Надо смотреть на нее как на определение энтропии.
Правда, Для того чтобы это определение получило конкретное содержание, надо дополнить его способами вычисления вероятностей состояний во всех требуемых случаях. Но и без этого видно, что при таком понимании энтропии закон ее возрастания коренным образом меняет свой характер. Он утрачивает свою абсолютность и превращается в статистический закон. Энтропия замкнутой системы может не только возрастать, но и убывать. И она действительно будет убывать, если только подождать достаточно долго.
Однако процесс убывания снова сменится в дальнейшем процессом возрастания. Что же остается в таком случае от второго начала термодинамики? В чем состоит его физическое содержание?
А в том, что за каким-либо заданным состоянием системы будут следовать состояния еще более вероятные, если и не с необходимостью, то в подавляющем большинстве случаев. Если система большая, а исходное состояние ее не очень близко к состоянию равновесия, то переходы системы в менее вероятные состояния будут настолько маловероятны, что на практике они совершенно не имеют никакого значения. Тогда закон возрастания энтропии оправдывается практически с абсолютной достоверностью.
Ранее обсуждалась концепция тепловой смерти Вселенной, выдвинутой Клаузиусом. Здесь следует заметить, что в противоположность этой концепции Больцманом была высказана так называемая флуктуационная гипотеза. Больцман не отрицал применимость второго закона термодинамики к Вселенной в целом.
Однако второе начало термодинамики есть статистический закон, согласно которому отступления от термодинамического равновесия — флуктуации — не только возможны, но и неизбежны.
Больцман считал, что неравновесное состояние Вселенной, в котором она находится сейчас,
117 |
Молекулярная физика |
есть гигантская флуктуация. Эта флуктуация должна исчезнуть. Тогда наступит состояние тепловой смерти Вселенной. Однако это состояние временное. Спустя некоторое время снова возникнет аналогичная гигантская флуктуация, и Вселенная выйдет из состояния тепловой смерти. Затем опять наступит тепловая смерть и так без конца. Если согласно концепции Клаузиуса тепловая смерть есть окончательное состояние Вселенной, из которого она никогда не может выйти, то по гипотезе Больцмана Вселенная периодически приходит в состояние тепловой смерти и самопроизвольно выходит из него. Однако времена между двумя последовательными гигантскими флуктуациями невообразимо велики по сравнению с временем существования каждой из них.
Поэтому можно сказать, что по флуктуационной гипотезе Вселенная должна находиться в состоянии тепловой смерти «почти всегда».
Мы видим, что флуктуационная гипотеза, радикально отличаясь от концепции Клаузиуса в принципиальном отношении, приводит практически почти к тому же окончательному результату.
Однако нельзя экстраполировать на Вселенную в целом второе начало термодинамики, если даже смотреть на него как на статистический закон.