Обозначим его первое перемещение радиус-вектором r1, второе r2 и так далее. После N перемещений матрос окажется в точке, задаваемой вектором R=r1+r2+..rN. Так как эти все векторы не связаны друг с другом никоим образом, то совсем непонятно, где окажется матрос. Однако, возведя это выражение в квадрат, и усредняя получим:

R2≈N r2

где r – перемещение до падения. Это мы уже проделывали выше.

Таким образом, после N шагов (то бишь, и падений) матрос окажется от кабачка на расстоянии R=√N r . Если r~1 м, то чтобы отойти от кабачка на 10 м, ему придется упасть 100 раз, а упав 10 тысяч раз, ему удастся удалиться только на 100 м!

3. «Ежик в тумане». Говорят, что в отсутствие ориентиров (солнце, звезды, шум шоссе или железной дороги и т.п.) человек бродит в лесу или по полю, в буране или в густом тумане кругами, всё время возвращаясь на прежнее место. На самом деле он ходит не кругами, а примерно так, как движутся молекулы или броуновские частицы. На прежнее место он вернуться может, но только случайно. А вот свой путь он пересекает много раз. Рассказывают также, что замерзших в пургу людей находили «в каком-нибудь километре» от ближайшего жилья или дороги, однако на самом деле у человека не было никаких шансов пройти этот километр, и вот почему.

Чтобы рассчитать, насколько сместится человек в результате случайных блужданий, надо знать величину l, т.е. расстояние, которое человек может пройти по прямой, не имея никаких ориентиров. Оказалось, что в среднем студент с завязанными глазами проходил по прямой всего лишь около 20 метров (отклонение от идеальной прямой не превышало 5°), а потом начинал все более отклоняться от первоначального направления. Пусть теперь человек идет (вернее, блуждает) в лесу со скоростью 2 километра в час (для дороги это очень медленно, но для густого леса – очень быстро), тогда, если ве-личина l равна 20 метрам, то за час он пройдет 2 км, но сместится всего лишь на 200 м, за два часа – примерно на 280 м, за три часа – 350 м, за 4 часа – 400 м и т. д. А двигаясь по прямой с такой скоростью, человек за 4 часа прошел бы 8 километров, поэтому в инструкциях по технике безопасности полевых работ есть такое правило: если ориентиры потеряны, надо оставаться на месте, обустраивать убежище и ждать окончания ненастья (может выглянуть солнце) или помощи.

6.5. Барометрическая формула. Закон Больцмана

Хаотические молекулярные движения приводят к тому, что частицы газа равномерно распределяются по объему сосуда, так что в каждой единице объема содержится в среднем одинаковое число частиц. В равновесном состоянии давление и температура газа также одинаковы во всем объеме. Но так обстоит дело только в том случае, когда на молекулы не действуют внешние силы. При наличии же таких сил молекулярные движения приводят к своеобразному поведению газов.

Рассмотрим, например, газ (воздух), находящийся под действием силы тяжести. Если бы отсутствовало тепловое движение молекул, то все они под действием силы тяжести «упали» бы на Землю, и весь воздух собрался бы тончайшим слоем у поверхности Земли.

Если бы отсутствовала сила тяжести, но существовали бы молекулярные движения, молекулы разлетелись бы по всему мировому пространству. Атмосфера, воздушная оболочка Земли, обязана своим существованием в ее теперешнем виде наличию

одновременно и теплового движения молекул, и силы притяжения к Земле. При этом в атмосфере устанавливается вполне определенное распределение молекул по высоте. Соответственно этому распределению молекул устанавливается и определенный закон изменения давления газа с высотой.

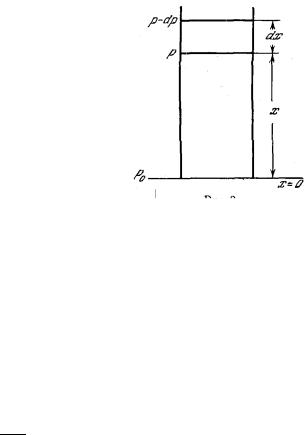
Рассмотрим вертикальный столб воздуха (рис.). Пусть у поверхности Земли, где х = 0, давление равно р0, а на высоте х равно р. При изменении , высоты на dx давление изменяется на

dp.

Давление воздуха на некоторой высоте равно весу вертикального столба воздуха, находящегося на этой высоте над площадью, равной единице. Поэтому dp равно разности весов столбов воздуха над площадью, равной единице, нр высотах х и х + dx,

т. е. равно весу столба воздуха высотой dx с площадью основания в одну единицу:

dp=−ρ gdx ,'

где ρ — плотность воздуха (масса единицы объема) и g — ускорение

силы тяжести. Плотность ρ газа равна произведению массы m молекулы на их число n в единице объема:

ρ=m n .

Из кинетической теории известно, что

p=nkT

Следовательно,

ρ= mk Tp

Тогда

dp=− mgkT p dx

или

dpp =− mgkT dx

Если считать, что температура на всех высотах одна и та же (что, вообще говоря, неверно), то, интегрируя это уравнение, получим:

ln p=− mgkT x+lnC p=C exp(− mgkT x)

где С — постоянная интегрирования.

Постоянная С определяется из условия, что при х=0 давление р = р0. Подставив в уравнение эти значения х и р, получим:

C=p0

Это уравнение, устанавливающее закон убывания давления с высотой, называется барометрической формулой. Из этого уравнения видно, что давление газа убывает с высотой по экспоненциальному закону. Этим законом пользуются для определения высоты над Землей путем измерения давления на данной высоте и на уровне моря

Приборы, служащие для измерения высоты горных вершин, полета самолета и т. д., представляют собой специальные барометры, шкала которых проградуирована непосредственно в метрах.

Так как давление газа, как мы видели раньше, пропорционально числу молекул п в единице объема (р = nkT), то барометрическая формула выражает также закон убывания плотности молекул с высотой:

n=n0 exp(− RμTg x)

где n и n0 — число молекул в единице объема в точках, между которыми разность высот равна х. Эта формула показывает, что атмосфера Земли должна простираться до бесконечности.

Однако мы не учли два обстоятельства:

1)температура с высотой меняется

2)атмосфера — неравновесная система.

Тем не менее этой формулой можно пользоваться до высот 60-70 км, учитывая оправки на то, что температура меняется с высотой.

Закон Больцмана

Полученная выше барометрическая формула относится к случаю, когда газ находится под действием силы тяжести. Величина mgx в формуле

(− m gx )

n=n0 e k T

представляет собой потенциальную энергию молекулы на высоте х. Можно поэтому сказать, что эта формула дает нам число частиц n, энергия которых

U = mgx,

если число частиц с энергией, равной нулю, равно n0 (высота х отсчитывается от нуля). Нет никаких оснований считать, что поведение газа существенно изменится, если вместо силы тяжести на него будет действовать какая-либо другая сила, а выражение для энергии будет иметь другой вид. Если газ находится в каком-нибудь силовом поле, так что его частицы обладают некоторой потенциальной энергией, то число частиц, обладающих заданной энергией U, определяется формулой

Эта формула называется формулой Больцмана, Она позволяет определить долю частиц, которые в условиях теплового равновесия обладают энергией U:

Из формулы (1) видно, что доля n/n0 частиц с данной энергией U, кроме величины этой энергии, зависит только от температуры.

Это позволяет трактовать и самую температуру несколько иначе, а именно как величину, от которой зависит, как распределяются частицы по энергиям.

При данной температуре доля молекул, обладающих той или иной энергией U, зависит от значения U и быстро уменьшается с ростом U. Это значит, что доля молекул с очень большой энергией всегда очень мала. И чем ниже температура, тем быстрее n/n0 убывает с ростом U.

6.6. Понятие о вероятности

Закон Больцмана, как и барометрическую формулу, удобно трактовать с несколько иной точки зрения, пользуясь понятием вероятности.

К этому термину, мы прибегаем в тех случаях, когда идет речь о случайных событиях, т. е. таких, условия наступления которых по тем или иным причинам неизвестны и которые поэтому нельзя заранее с уверенностью предсказать.

Бросая много раз монету, мы можем быть уверены, что приблизительно в половине случаев она упадет обращенной вверх стороной с гербом. И это будет тем вероятнее, чем больше будет число бросаний. Тогда мы можем сказать, что вероятность выпадания герба равна ½.

Эти и другие подобные им опыты позволяют нам дать следующее определение вероятности: вероятностью события называется предел, к которому стремится отношение числа опытов, приводящих к его осуществлению, к общему числу опытов при беспредельном увеличении последнего.

Вероятность W этого события выражается формулой:

W= lim N ' .

N

Где N – общее число опытов, а N' – когда выпадает герб. Аналогичная вероятность того, что выпадет решка. Сумма этих двух вероятностей равна единице. Вероятность, равная единице, означает достоверность события. Наоборот, если какое-то событие невозможно (например, монета не упала на землю), то его вероятность равна нулю.

Но так бывает не всегда. Например, из того факта, что при выстреле в цель возможно лишь два исхода — попадание или промах, не следует, что вероятность попадания равна 1/2, так как попадание и промах не являются равновозможными результатами. Однако, хотя вероятности каждого из двух возможных исходов выстрела и не равны, их сумма (для данного стрелка) и в этом случае равна единице: о том, что выстрел приведет к какому-то исходу — попаданию или промаху, можно утверждать с полной определенностью!

Теорема сложения вероятностей. Рассмотрим теперь еще один пример, который позволит нам сформулировать одно из важных положений теории вероятностей и,

кроме того, дать еще одно определение самой величины вероятности. Оно будет нам полезно в дальнейшем.

Пусть в ящике лежат 20 вполне одинаковых по своим размерам и весу гладких шаров и пусть 5 из них выкрашены в белый цвет, а остальные — в черный.

Вероятность вытянуть шар любого цвета равна, очевидно, 1/20. Какова вероятность того, что будет вынут белый шар?

Так как для каждого шара (все равно, белого или черного) вероятность быть вынутым равна 1/20, а всего белых шаров пять (и нам все равно, какой из них будет вынут), то искомая вероятность равна сумме вероятностей для всех белых шаров:

W= 201 + 201 + 201 +201 + 201 = 205

Этот результат выражает одно из положений теории вероятностей — теорему сложения вероятностей, которая гласит:

если W1, W2, W3 и т. д. — вероятности нескольких исключающих друг друга событий, то вероятность того, что осуществится какое-нибудь одно из них, равна сумме вероятностей всех этих событий.

Значит, сумма вероятностей нескольких событий дает нам вероятность того, что наступит или одно событие, или другое, или третье и т. д. При этом предполагается, что эти события, или хотя бы два из них, не могут произойти одновременно. Так, в нашем примере 5/20 -— это вероятность того, что будет вынут один из белых шаров, а так как операция извлечения шара производится только один раз, то если вынут один какой-нибудь белый шар, то не может быть вынут никакой другой.

Приведенный пример позволяет дать новое определение вероятности, несколько отличающееся от прежнего:

как отношение числа случаев, благоприятствующих его наступлению, к общему числу возможных случаев, если все случаи равновозможны.

Это определение вероятности принадлежит Лапласу. Оно не противоречит прежнему определению. Для приведенного только что определения вероятности существенно, чтобы все случаи были равновозможны, равновероятны.

При физических применениях теории вероятностей обычно тоже приходится иметь дело с равновероятными событиями. Вернемся теперь к формуле закона Больцмана

(1). Из того, что здесь было сказано о вероятности, ясно, что величина n/n0 в этой формуле как раз и имеет смысл вероятности. Ведь любая из n0 молекул может обладать потенциальной энергией U. Значит, n0 — это общее число возможных случаев. В действительности же энергией U обладают n молекул. Следовательно, n — это число, которое мы раньше назвали числом «благоприятствующих» случаев. Поэтому отношение n/n0, которое мы называли (и с полным основанием) долей молекул, обладающих энергией U, есть в то же время и вероятность

того, что любая из n0 молекул обладает такой энергией.

Теорема умножения вероятностей.

Она относится к случаю, когда определяется вероятность сложного события, состоящего в совмещении двух или больше независимых событий. События

называются независимыми, если вероятность любого из них не зависит от того, наступит или не наступит любое другое.

Например, поставим такую задачу: какова вероятность того, что стрелок, отправляясь к стрельбищу на трамвае, приобретет билет с четным номером, а вслед затем его первый выстрел увенчается попаданием? Ясно, что эти два события являются независимыми.

Допустим, что для нашего стрелка вероятность W1 попадания равна 0,8. Это значит, что в среднем из 10 посещений стрельбища он в восьми случаях первым выстрелом попадает в цель. Но при этом только в половине из них он приобретет в то же время билет с четным номером, так как вероятность W2 получить четный билет равна 1/2. Значит, искомая вероятность Wn сложного события — совпадения четного номера и успешного выстрела — равна произведению вероятностей каждого из них:

W12=W1 W2=0,8 0,5=0,4

Вероятность совмещения двух или нескольких независимых событий равна произведению вероятностей каждого из них в отдельности.

Вероятность и средние значения величин.

Cредние значения физических величин тоже тесно связаны с понятием вероятности. Пусть требуется определить некоторую величину а, относящуюся к системе или к любой ее части.

Пусть произведено N однотипных измерений одной и той же величины а при неизменных условиях. Пусть в N1 случаях измеренное значение величины а оказалось равным а1, в N2 случаях — а2 , в пт случаях — ат (N1+N2+..Nm = N). Среднее значение измеряемой величины определяется выражением

a= a1 N1 +a2 N2 +...+am Nm =ν1 a1 +νa2+...+νm am

N

если неограниченно увеличивать число измерений N, то частоты vx, перейдут в свои предельные значения W — вероятности появления при измерениях значений а1, а2 ат. Выражение при этом переходит в

M {a}=a=W1 a1 +W2 a2 +...+Wm am

Сумма называется математическим ожиданием величины а.

Случайные непрерывные величины. Функция распределения

Непрерывной называют случайную величину, которая может принимать значения из некоторого конечного или бесконечного интервала.

Для случайной непрерывной величины введем функцию распределения:

Функцией распределения называют функцию F(x) определяющую вероятность того, что случайная величина X в результате испытания примет значение меньшее х

F(x)=W ( X <x)

Свойства функции F(x)

1)0 F (x)1

2)Из теоремы сложения вероятностей следует

F(x1 )−F (x2 )=P(x1≤X ≤x2)