66 |
Молекулярная физика |
Найдем дифференциальное уравнение, которому удовлетворяет вектор j в одномерных задачах.
Пусть имеется неограниченная среда, в которой происходит поток тепла в направлении, параллельном оси X. В общем случае свойства среды могут меняться в том же направлении. Кроме того, они могут меняться во времени. Поэтому плотность потока тепла J следует рассматривать как функцию координаты х и времени t:
.
J =J (x ,t)
Для одномерного случая J- скалярная величина
S — площадь поперечного сечения цилиндра Через боковые стенки тепло не передается
Выделим мысленно в среде бесконечно длинный цилиндр с образующими, параллельными оси X, и рассмотрим бесконечно малый участок такого цилиндра АВ с
длиной dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Через сечение A поступает тепло |
J (x ,t) S dt - по определению |
|
||||||||||||||
Через сечение B выходит тепло |
J (x+dx ,t )S dt |
|
|
|
||||||||||||
Поглощенное тепло в объеме |
(J (x ,t )−J (x+dx ,t ))S dt |
|
||||||||||||||
Тогда |
|
|
|
|
|
|
∂ J |
|
|
|
|
|
|
|
|
|
(J (x ,t )−J (x +dx ,t ))S dt=− |
S dx dt |
|
|
|
|
|
|
|||||||||
∂ x |
|
|
|
|
|
|
||||||||||
поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dm=ρ( x)dV =ρ(x) S dx . |
|
|
|
|||||||||||||
δ Q=dmcV dT , |
|
|
|
|||||||||||||
получим уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ρ(x)cV |
S dx dT =− |
∂ J |
S dxdt |
или |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
∂ x |
|
|
|
|
|
∂T |
|
∂ J |
|
|
||
|
|
|
|
|
|
|
|
|
|
ρ(x)c |
V |
=− |
(1) |
|||
|
|
|
|
|
|
|
|
|
|
|
∂ x |
|||||
|
|
|
|
|
|
|
|
|
|
|
∂ t |
|
||||
Если учесть уравнение состояние идеального газа |
|
|||||||||||||||
PV |
m |
|
ρ |
RT |
, то (1) можно переписать в виде: |
|
||||||||||
= μ |
RT , P=μ |
|
||||||||||||||
∂T |
=− RT ∂ J |
- |
эта |
величина используется в задачах моделирования |
климата |
|||||||||||
∂ t |
|
pμ ∂ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(скорость радиационного нагрева атмосферы) и определяет как солнечное излучение нагревает атмосферу Земли.
67 |
Молекулярная физика |
3. Теперь надо установить связь между плотностью потока тепла и температурой среды Т.
Опыт показывает, что поток тепла имеет место только тогда, когда температура среды меняется от точки к точке. Тепло течет всегда в направлении от высшей температуры к низшей. Простейшим является случай бесконечной однородной пластинки толщины l.
Если на одной стороне пластинки поддерживается температура Т1 а на другой — температура Т2, причем
Т1 > Т2 , то опыт показывает, что поток тепла пропорционален разности температур (Т1 - Т2) и обратно пропорционален толщине пластинки l. Математически это можно представить в виде:
J =κ |
T 1−T 2 |
(2) |
|
l |
|||
|
|
где κ. — положительная постоянная, зависящая только от материала пластинки и его физического состояния. Эта постоянная называется коэффициентом теплопроводности.
Допустим, что пластинка бесконечно тонкая. Если ось X направлена в сторону понижения температуры, то
l = dx, Т1 = Т(х), Т2 = Т(х+dx),
|
T 1−T 2 |
= |
∂T |
|
||
|
l |
∂ x |
|
|||
|
|
|
||||
и формула (2) переходит в |
|
|
|
|
||
J =−κ |
∂ T |
|
(3) |
|||
|
||||||
|
|
|
∂ x |
|
||
Выражение справедливо и в общем случае неоднородной среды с совершенно произвольным распределением температуры. Коэффициент теплопроводности является функцией х Если выражение (3) подставить в формулу (1), то получится
|
∂T |
|
∂ |
|
∂T |
|
|
ρ cV |
|
= |
(κ |
|
) |
(4) |
|
∂t |
∂ x |
∂ x |
|||||
Это уравнение называется уравнением теплопроводности.
В частном случае, когда среда однородна (нет зависимости от х) и коэффициент κ не зависит от температуры, оно принимает вид
ρ cV |
∂T |
=κ |
∂2 T |
(5) |
или |
∂t |
|
∂ x2 |
|
|
|
|
|
|
∂T =χ ∂2 T |
(6) |
|||
∂ t |
∂ x2 |
|
||
где введено обозначение |
|
κ |
|
(7) |
|
χ= |
|
||
|
ρ cV |
|
||
|
|
|
|
|
Постоянная χ называется коэффициентом температуропроводности среды.
68 |
Молекулярная физика |
В среде могут оказаться источники тепла. Например, тепло может выделяться в результате прохождения электрического тока или радиоактивного распада. Такие источники мы не принимали во внимание. Чтобы их учесть, введем величину q, равную количеству тепла, выделяемому источниками в единице объема среды в одну секунду. Тогда вместо уравнения (1) следует писать
ρ(x)c |
V |
∂T |
=− |
∂ J |
+q |
(8) |
|
∂ t |
∂ x |
||||||
|
|
|
|
В соответствии с этим изменятся и остальные уравнения.
4. В общем случае, когда свойства и температура среды зависят
от всех трехпространственных координат х, у, z, уравнение теплопроводности, выражающее баланс тепла в теле, имеет вид
|
∂T |
|
∂ J x |
|
∂ J y |
|
∂ J z |
|
|
ρ(x)cV ∂ t |
=−(∂ x |
+ |
∂ y |
+ |
∂ z |
)+q=( , J )+q |
(9) |
||
Однако решения такого уравнения аналитически можно получить только в простейших случаях. Наиболее важными являются случаи, когда среда и распределение температуры в ней обладают сферической или цилиндрической симметрией.
Рассмотрим сначала случай сферической симметрии.
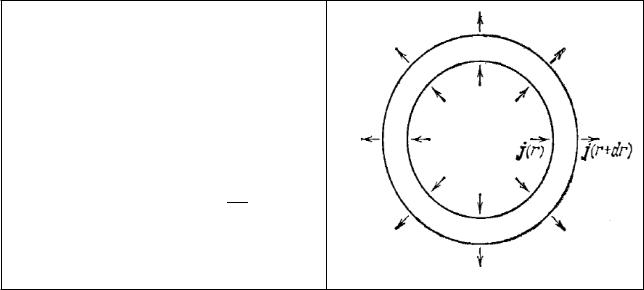
Вектор плотности потока тепла J направлен вдоль радиуса, причем величина J, помимо времени, зависит только от r. Опишем вокруг центра симметрии две концентрические сферы с радиусами r и r + dr (рис. 2).
Количество тепла, поступающее через первую сферу за время dt
J (r)4 π r2 dt=4 π(r2 J )r dt
Количество тепла, вытекающее (поглощенное) за то же время через вторую, сферу
J (r+dr)4 π(r+dr)2 dt=4 π(r2 J )r +dr dt |
|
Количество тепла втекающее |
в |
сферический слой: |
|
4 π[(r2 J )r −(r2 J )r+ dr ]dt=4 π ∂∂r (r2 J )dr dt
Рис.2
При наличии распределенных источников сюда надо добавить количество тепла
q (r)4 π r2 dr dt ,
поставляемое источниками.
Изменение количества тепла в слое можно представить в виде
ρ 4π r2 dr cV dT.
69 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Молекулярная физика |
|
Тогда уравнение баланса тепла будет |
|
|
|
|
|
|
|
||||||||||||
ρ cV |
∂T |
=− |
1 |
|
|
∂ |
|
(r2 J )+q |
(10) |
||||||||||
∂t |
r2 ∂ r |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Если учтем формулу (3) J =−κ |
∂ T |
|
|
и ее перепишем в виде |
|
||||||||||||||
∂ x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂ T |
|
|
||||||||
|
|
|
|
|
|
J =−κ |
|
||||||||||||
тогда (10) принимает вид: |
|
|
|
|
|
∂ r |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∂T |
1 |
|
|
|
|
|
|
|
|
|
∂T |
|
|||||||
|
|
∂ |
|
2 |
|
|
|||||||||||||
ρ cV |
|
= |
|
|
(r |
|
|
κ |
|
)+q |
(11) |
||||||||
∂t |
r2 |
∂r |
|
|
∂ r |
||||||||||||||
Аналогичные рассуждения проводятся и в случае цилиндрической симметрии. Понимая теперь под r расстояние до оси симметрии, получим
ρ cV |
∂T |
=− |
1 |
∂ |
(r J )+q |
|
|
|
(12) |
||
∂t |
r ∂ r |
(r κ |
|
)+q |
|||||||
|
|
|
|
|
|
|
|||||
|
|
ρ cV |
∂T |
1 |
∂ |
∂ T |
(13) |
||||
|
|
|
|
= r |
|
||||||
|
|
∂t |
|
∂ r |
∂ r |
||||||
5. К уравнению теплопроводности надо добавить общее соотношение, которое должно выполняться на границе раздела двух произвольных сред. Это граничное условие состоит в том, что по обе стороны указанной границы должны быть одинаковые нормальные составляющие вектора J.
Вырежем на границе двух сред бесконечно-тонкий цилиндр.
п — единичный вектор нормали к ней, проведенный от первой среды ко второй.
Высота цилиндра h должна быть бесконечно малой высшего порядка по сравнению с линейными размерами оснований. Тогда потоком тепла через боковую поверхность цилиндра можно пренебречь.
Если S — площадь основания цилиндра, то количество тепла, вступающее в него в 1 секунду, будет равно
(J (n1)(r)−J(n2)(r+h))S
Но эта величина, как и количество тепла, содержащееся в цилиндре, должна быть пропорциональна его объему
V=Sh,
т. е. в пределе при h → 0 должна обращаться в нуль. Таким образом, в пределе, когда оба основания цилиндра сливаются друг с другом на границе раздела сред, должно быть
J(n1)(r)=J(n2)(r) |
(14) |
Это значит, что на любой границе нормальная составляющая вектора потока тепла непрерывна.
Доказательство предполагает, что на границе раздела сред нет источников тепла с конечной поверхностной плотностью. При наличии таковых нормальная составляющая При наличии таковых нормальная составляющая вектора J может претерпевать разрыв.