1.6.5.1 Корректирующие коды

Корректирующие коды используются в каналах с помехами для получения достоверности принимаемой информации. Код называется корректирующим, если он позволяет обнаруживать или обнаруживать и исправлять ошибки. Чтобы код обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные символы (избыточные). Чем больше избыточность кода, тем выше его корректирующая способность.

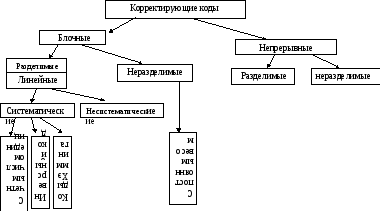
Рис.1.28. Классификация корректирующих кодов

1.Блочные кодыхарактеризуются тем, что последовательность передаваемых символов разделены на блоки. Операции кодирования и декодирования производится отдельно.

2.У непрерывных кодов– первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

3.В разделимых кодахможно выделить информационные и контрольные символы, которые служат для коррекции ошибок.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Их особенности в том, что контрольные символы образуются как линейные комбинации информационных символов.

Все линейные систематические коды являются групповыми.

Групповые коды - характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю 2 любой пары комбинаций дает комбинацию принадлежащую этой группе.

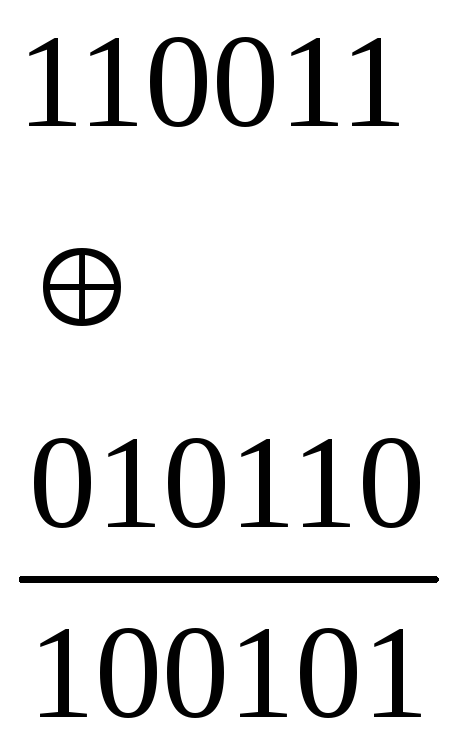
Т.е расстояние между двумя комбинациями(110011) и(010110) определяется количеством единиц в их сумме по модулю два:

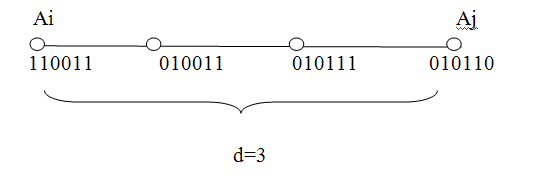
В общем случае пара разрешенных комбинаций Ар1иАр2, разделенных кодовым расстояниемdбудет изображаться на прямой точками запрещенных комбинаций (рис.1.29).

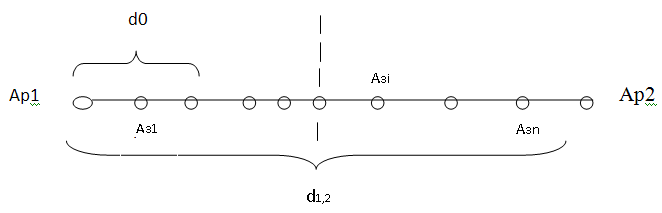
Рис. 1.29. Расстояние между двумя кодовыми комбинациями

Для того чтобы в результате ошибки комбинация Ар1преобразовалась в другую разрешеннуюАр2, должно исказитьсяdсимволов. При искажении меньшего числаАр1перейдет в запрещенную комбинацию и ошибка будет обнаружена. Т.е ошибка всегда обнаруживается если её кратность, т.е число искаженных символов “g” будет :

_.

_{Минимальное кодовое расстояние, при котором обнаруживаются одиночные ошибки:}

_{d0 = 2}

_{Если ошибка в символах комбинации происходят независимо друг от друга, то вероятность искажения “g” символов в n - значной комбинации будет:}

где - вероятность искажения одного символа, т.к,то вероятность многократных ошибок уменьшается с увеличением их кратности.

Наиболее вероятны меньшие расстояния. Исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается принятой ближайшая разрешенная. Это правило декодирования для указанного распределения будет оптимальным. При этом правиле все ошибки кратности

_.

Минимальное d? при котором ещё можно исправлять одиночные ошибки равно:

Корректирующие способности кода возрастает с увеличением d.При фиксированном числе разрешенных комбинацийувеличениеdвозможно лишь за счет роста количества запрещенных комбинаций.

_.

Что в свою очередь требует избыточного числа символов:

_{где k - количество символов в кодовой комбинации без избыточности.}

_{Можно ввести понятие избыточности кода}

.

_{При независимых ошибках количество всевозможных сочетаний g ошибочных комбинаций определяется формулой числа сочетаний:}

_.

_{Тогда полная вероятность ошибок кратности g учитывает все сочетания будет:}

гдевероятность искаженности одиночного символа. Вероятность правильного приёма всехnбудет равна:

.

_{А вероятность правильного корректирования будет равна:}

_.

_{Здесь суммирование по всем значениям кратности ошибок, которые обнаруживаются и исправляются. Таким образом:}

_.

Анализ этой формулы показывает, что при малой величине и большихnнаиболее вероятны ошибки малой кратности и их необходимо корректировать в первую очередь. Вероятность,избыточностиϰ и число символовn- основные характеристики корректирующего кода. Задача при создании кода-достижение минимальных значенийиϰ.

Целесообразность применения того или иного кода зависит также от сложности кодирования и декодирования устройств. В соответствии с общим принципом корректировки ошибок необходимо сравнивать принятую комбинацию со всеми комбинациями этого кода. Этот способ требует сложных устройств.

Поэтому на практике чаще всего используются коды, которые позволяют с помощью ограниченного числа преобразований принятых кодов символов извлечь всю необходимую информацию о корректируемых ошибках.