1.4.1.1 Спектр амплитудно-модулированного колебания

Пусть задано высокочастотное модулированное колебание, о котором известно, что частота (ω₀ и начальная фаза θ₀ величины постоянные, а огибаю­щая A(t) содержит в себе передаваемое сообщение s(t). Аналитически такое колебание можно представить с помощью выражения (1.88).

Требуется установить связь между спектром модулированного колеба­ния и спектром модулирующей функции, т. е. спектром исходного сообще­ния s(t). Проще и нагляднее всего это можно сделать для тональной (гармо­нической) модуляции, когда огибающая

а модулированное колебание определяется выражением (1.90).

Перепишем выражение (1.90) в форме

.

Второе слагаемое в правой части этого выражения, являющееся продук­том модуляции, можно привести к виду

.

после чего развернутое выражение колебания a(t) принимает вид

Первое слагаемое в правой части представляет собой исходное немодулированное колебание с частотой ω₀. Второе и третье слагаемые соответст­вуют новым колебаниям (гармоническим), появляющимся в процессе модуля­ции амплитуды. Частоты этих колебаний ω₀ + Ω и ω₀ - Ω называются верхней и нижней боко­выми частотами модуляции.

Амплитуды этих двух колебаний одинаковы и составляют от амплитуды немодулированного колебания долю, равную М/2, а их фазы сим­метричны относительно фазы несущего колеба­ния. Это иллюстрируется векторной диаграм­мой, представленной на рис. 1.10 . На этой диаг­рамме ось времени вращается по часовой стрел­ке с угловой частотой ω₀, причем отсчет угла ω₀t ведется от линии ОВ.

Поэтому несущее ко­лебание А₀cos(ω₀+ θ₀) изображается на этой диаграмме в виде неподвижного вектора OD длиной A₀, составляющего с горизонталью уголθ₀. Мгновенное значение несущего колебания в момент t равно проекции вектора A₀ на ось времени (отрезок ОК).

Рис.1.10. Векторная диаграмма амплитудно-модулированного колебания

Для представления на этой же диаграмме колебания с частотой ω₀ + Ω, превышающей угловую частоту вращения оси времени на величину Ω, не­обходимо воспользоваться вектором, вращающимся с угловой частотой Ω против часовой стрелки (вектор DC₁). Для изображения колебания с часто­той ω₀ - Ω потребуется вектор, вращающийся с такой же частотой Ω по часовой стрелке (вектор DC₂). Поэтому колебания боковых частот— верх­ней и нижней — изображаются двумя векторами длиной MA₀/2, вращаю­щимися во взаимно противоположных направлениях. Начала этих векторов перенесены из точки О в точку D. Их фазы симметричны относительно век­тора несущего колебания А₀.

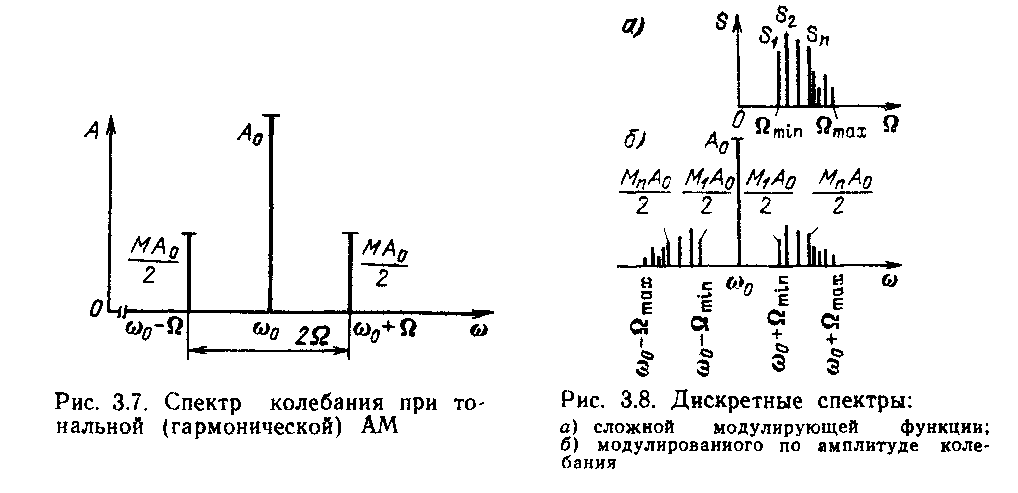Спектральная диаграмма колебания при тональной модуляции показа­на на рис. 1.9. Ширина спектра в этом случае равна удвоенной частоте модуляции 2Ω, а амплитуды колебаний боковых частот не могут превышать половины амплитуды не смодулированного колебания (при М≤ 1).

Аналогичные результаты можно получить при модуляции любым слож­ным сигналом.

Рис.1.11.Спектр колебания при тональной (гармонической) АМ

1.4.2 Угловая модуляция. Фаза и мгновенная частота колебания

Для простого гармонического колебания

набег фазы за какой-либо конечный промежуток времени от t = t₁доt =t₂равен

_.(1.91)

Отсюда видно, что при постоянной угловой частоте набег фазы за какой-ли­бо промежуток времени пропорционален длительности этого промежутка.

С другой стороны, если известно, что набег фазы за время t₂ - t₁ра­вен, то угловую частоту можно определить как отношение

, (1.92)

если, конечно, имеется уверенность, что в течение рассматриваемого про­межутка времени частота сохраняла постоянное значение.

Из (1.92) видно, что угловая частота есть не что иное, как скорость изменения фазы колебания.

Переходя к сложному колебанию, частота которого может изменяться во времени, равенства (1.91), (1.92) необходимо заменить интегральным и дифференциальным соотношениями

, (1.93)

. (1.94)

В этих выражениях ω(t) = 2πf(t)— мгновенная угловая частота колеба­ния;f(t)- мгновенная частота.

Согласно выражениям (1.93), (1.94) полную фазу высокочастотного ко­лебания в момент tможно определить как

, (1.95)

где первое слагаемое в правой части определяет набег фазы за время от начала отсчета до рассматриваемого момента t;- начальная фаза ко­лебания (в моментt= 0).

При таком подходе фазу ψ(t) = ω₀t + ϴ(t),фигурирующую в вы­ражении (1.85), следует заменить наψ(t) = ω₀t +ϴ (t) - ϴ₀.

Итак, общее выражение для высокочас-тотного колебания, амплиту­да которого постоянна, т. е. A (t)= А₀, а аргумент ψ(t) модулирован, можно представить в форме

. (1.96)

Соотношения (1.94), (1.95), устанавливающие связь между изменения­ми частоты и фазы, указывают на общность двух разновидностей угловой мо­дуляции — частотной и фазовой.

Поясним соотношения (1.94) - (1.96) на примере простейшей гармониче­ской ЧМ, когда мгновенная частота колебания определяется выражением

, (1.97)

где = 2πf_дпредставляет собой амплитуду частотного отклонения. Для краткости сод в дальнейшем будем называтьдевиацией частоты или простодевиацией.Через ω₀и, как и приAM, обозначены не­сущая и модулирующая частоты.

Составим выражение для мгновенного значения колебания (тока или напряжения), частота которого изменяется по закону (1.97), а амплитуда постоянна.

Подставляя в (1.95) ω(t) из уравнения (1.97), получаем

Выполнив интегрирование, найдем

. (1.98)

Таким образом,

. (1.99)

Фаза колебания, a(t)наряду с линейно-возрастающим слагаемымω₀(t)содержит еще периодическое слагаемое. Это позволяет рассматриватьa(t) как колебание,модулированное по фазе.Закон этой модуляции является интегральным по отношению к закону изменения ча­стоты. Именно модуляция частоты по законуприводит к модуля­ции фазы по закону. Амплитуду изменения фазы

(1.100)

часто называют индексом угловой модуляции.

Заметим, что индекс модуляции совершенно не зависит от средней (немодулированной) частоты ω₀, а определяется исключительно девиацией ω_ди модулирующей частотой.

Рассмотрим теперь противоположный случай, когда стабильное по ча­стоте и фазе колебание пропускается через устройство, осуществляющее

периодическую модуляцию фазы по закону , так что колебание на выходе устройства имеет вид

. (1. 101)

Какова частота этого колебания? Используя выражение (1.94), находим

. (1.102)

Учитывая соотношение (1.100), приходим к выводу, что . Таким образом, гармоническая модуляция фазы с индексомэквивалент­на частотной модуляции с девиациейω_д = Ω ϴ_max .

Из приведенного примера видно, что при гармонической угловой моду­ляции по характеру колебания нельзя заключить, с какой модуляцией мы имеем дело — с частотной или фазовой. В обоих случаях вектор ОА, изо­бражающий на векторной диаграмме модулированное колебание, качается относительно своего исходного положения таким образом, что уголϴ(рис. 1.12) изменяется во времени по законупри фазовой модуляции, при частотной модуляции (когда). ЦифрамиI, II, III и IV отмечено положение вектораОАприи 3π/2.

Рис.1.12 представление высокочастотного колебания при угловой модуляции в виде качающегося вектора

При гармоническом модулирующем сигнале различие между ЧМ и ФМ можно выявить, только изменяя частоту модуляции.

При ЧМ девиация ω_дпропорциональна амплитуде модулирующего на­пряжения и не зависит от частоты модуляцииΩ.

При ФМ величина ϴ_maxпропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции Ω.

Эти положения поясняются рис.1.13, на котором показаны частотные характеристики величин ω_дипри частотной и фазовой модуляциях. В обоих случаях предполагается, что на вход модулятора подается модули­рующее напряжение с неизменной амплитудойU, а частота _Ωизменяется от_Ωminдо_Ωmax.

При ЧМ ω_д, зависящая, как указывалось выше, только от амплитудыU,будет постоянной величиной, а индекс модуляциит– ω_д/=ϴ_maxcувеличением частоты будет убывать (рис. 1.11,а).При ФМтне зависит от , а ω_д= ϴ_max=mизменяется пропорционально частоте модуляции (рис. 1.11, б).

Рис.1.13. Зависимость индекса θ_max и девиации ω_д от модулирующей частоты

при ЧМ (а) и ФМ (б)

Кроме структуры колебания (при модуляции сложным сигналом) ча­стотная и фазовая модуляции различаются и способом осуществления. При ЧМ обычно применяется прямое воздействие на частоту колебаний генера­тора. При ФМ генератор дает стабильную частоту, а фаза колебания модули­руется в одном из последующих элементов устройства.