Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

§ 18.2), вычисляем потом по (19.15) и величину х°, которая будет в результате зависеть от формы нелинейности, от параметров системы и от внешнего воздействия М°.

Величина х° и является искомой статической или скоростной ошибкой соответственно для статической и астатической систем.

В тех случаях, когда передаточная функция линейной части системы R(р)/Q(p) имеет нулевой корень в знаменателе (что часто бывает), т. е. когда Q(0) = 0, вместо (19.14) получаем уравнение

(19.16)

откуда определяется статическое отклонение или скоростная ошибка х°(М°). В случае, когда при отсутствии внешнего воздействия (М° = 0) определяются автоколебания в системе с несимметричной нелинейностью, т. е. нелинейностью F(х) или же F(х, рх), для которой

(19.17)

вместо уравнения (19.8) получаем

(19.18)

Оно решается любым из тех же двух методов, описанных выше для уравнения (19.8). Одновременно согласно (19.11) определяются х°, ап, wп.

Если в этом случае знаменатель Q(р) передаточной функции линейной части системы имеет нулевой корень, то Q(0) = 0 и, следовательно, уравнение (19.18) с учетом (19.13) принимает вид

(19.19)

откуда определяется х°. Это означает, что в указанных системах возникает такое смещение х° колебаний переменной х, которое ликвидирует свойственную данной нелинейности несимметрию колебаний переменной F(т. е. обеспечивается F° = 0), как показано, например, на рис. 19.4 в отличие от рис. 19.1, б.

Приведем пример исследования совместного влияния двух внешних воздействий, причем из дальнейшего будет видно, что, в отличие от линейных систем, здесь нельзя просто складывать статические ошибки от отдельно взятых воздействий.

Уравнения автоматической системы заданы в виде

(19.20)

(19.21)

(19.22)

где F(х) — простейшая симметричная релейная характеристика, показанная на рис. 19.5:

(19.23)

Чтобы воспользоваться выведенными выше общими формулами, надо сначала привести

заданную систему уравнений (19.20) — (19.22) к одному уравнению типа (19.1). В результате получаем

(19.24)

Пусть f1(t) является задающим воздействием, изменяющимся с постоянной скоростью:

(19.25)

которое требуется воспроизвести на выходе системы в виде x4(t). Допустим также, что второе внешнее воздействие f2(t) является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы);

(19.26)

Его влияние требуется свести к минимуму. Найдем установившуюся ошибку на выходе системы. Правая часть уравнения (19.24) будет при этом постоянной, и установившееся решение для х с учетом автоколебаний в виде

(19.27)

Гармоническая линеаризация нелинейности (19.23) при этом согласно (19.6) дает

(19.28)

В данной задаче согласно (19.24) уравнение (19.9) для периодических составляющих получит вид

(19.29)

а уравнение (19.8) для постоянных составляющих будет

(19.30) где согласно (19 24)— (19.26)

(19.31)

Выше были указаны два метода решения задачи. Для иллюстрации обоих методов решим данную задачу каждым из них.

Согласно первому методу сначала решается уравнение (19.29) для определения зависимостей а(х°) и w(х°).

Характеристическое уравнение здесь будет

(19.32)

и уравнения (19.11) поэтому примут вид

(19.33)

Исключая отсюда q, находим частоту автоколебаний

(19.34)

Частота w в данной задаче оказалась не зависящей от смещения х°, а следовательно, и от величины внешнего воздействия. Затем, подставляя в первое из уравнений (19.33) выражение q из (19.28) и w2 из (19.34), получаем биквадратное уравнение для отыскания зависимости амплитуды автоколебаний аи от смещения х°:

(19.35)

где величина

(19.36)

представляет собой амплитуду автоколебаний в данной системе при отсутствии смещения (при х° = 0). Отсюда

(19.37)

Полученное выражение можно записать также в виде

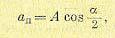(19.38)

если обозначить

(19.39)

Результат (19.37) или (19.38) и представляет собой искомую зависимость ап (x°). Далее, согласно первому методу решения задачи подставим полученное значение амплитуды ап из (19.38) в выражение (19.28) для F°, откуда с использованием (19.39) найдем функцию смещения

(19.40)

где А определяется через параметры системы формулой (19.36).

Подставив величину (19.40) в уравнение (19.30) для постоянных составляющих, с учетом (19.31) и (19.36) получим

(19.41)

Сравнивая это с формулой (19.39), видим, что для искусственно введенной ранее величины а можно записать следующее выражение:

(19.42)

Эта величина характеризует совокупность приложенных к системе внешних воздействий. Учитывая это, из формулы (19.38) находим амплитуду автоколебаний

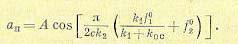(19.43)

Существенно то, что амплитуда автоколебаний зависит не только от параметров системы (см. (19.36)), но еще и от величины внешних воздействий. Эта зависимость нелинейная. В данном случае при увеличении внешних воздействий амплитуда уменьшается по закону косинуса, в то время как частота не зависит от внешних воздействий.

Из формулы (19.43) видно, что автоколебания существуют до тех пор, пока величины внешних воздействий удовлетворяют условию

(19.44)

При этом амплитуда автоколебаний изменяется в пределах А > aп > 0.

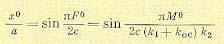
где А выражается только через параметры системы согласно (19.50).

Важно отметить, что функция смещения Ф(х°) не зависит ни от числа внешних воздействий, ни от характера их изменения (если они постоянные или медленно меняющиеся), что наиболее наглядно было видно из первого метода решения задачи. Итак, двумя разными методами определена величина смещения х° автоколебаний на входе реле. Найдем теперь установившуюся ошибку на выходе системы x4. Поскольку на выходе должно воспроизводиться внешнее воздействие f1(t), то согласно рис. 19.5 и второму уравнению (19.20) ошибка данной системы выражается величиной х1, установившееся решение для которой, следовательно, и надо искать. Выразив переменную х1 через х, которая уже известна, из заданных уравнений системы (19.20) и (19.21) получаем

Учитывая (19.25) и (19.27), перепишем данное уравнение в виде

(19.54)

В соответствии с видом правой части установившееся решение этого линейного уравнения следует искать в виде

(19.55)

где х1 и с1 — постоянные, а х* — периодическая составляющая.

Подставив это в (19.54), получим три уравнения для отыскания указанных величин:

(19.56)

(19.57)

(19.58)

Второе из них дает

(19.59)

Тогда из (19.56) находим

(19.60)

где x° определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной x4:

(19.61)

где ап определяется формулой (19.49) через внешнее воздействие, а wп — формулой

(19.48).

Итак, в данной системе имеются все три составляющие ошибки (19.55), зависящие от величины внешних воздействий и от параметров системы. Наиболее нежелательной из них является составляющая с1t, возрастающая пропорционально времени. Поэтому систему необходимо видоизменить в первую очередь так, чтобы уничтожить эту составляющую ошибки, т. е. сделать с1 = 0. Для этого можно было бы вовсе изъять дополнительную обратную связь (рис. 19.5), так как при kос = 0 согласно (19.59) будет с1= 0. Однако при этом существенно возрастает амплитуда автоколебаний (19.61), т. е. периодическая составляющая ошибки. Поэтому более целесообразной мерой будет замена жесткой обратной связи хос = kосx4 на гибкую хос = kосрx4. Тогда в уравнении (19.54) величина kос заменится на kоср:

(19.62)

Как видим, составляющая, пропорциональная времени, в правой части уравнения исчезла, вследствие чего установившееся решение для ошибки х1, в отличие от (19.55), будет

соответственно для медленно меняющейся составляющей и для колебательной составляющей. При этом разделении уравнений, как и прежде, сохраняются существенно нелинейные свойства системы.

Следовательно, здесь сохраняется целиком прежний (§ 19.1) первый метод решения задачи (второй здесь неприемлем), выраженный формулами (19.10) — (19.13), где в данном случае х° является величиной не постоянной, а медленно меняющейся. Поэтому прежний процесс решения заканчивается определением функции смещения (19.13). Подставив (19.13) в (19.66), получим дифференциальное уравнение для определения медленно меняющегося сигнала управления х° (t) (на фоне автоколебаний системы) в виде

(19.68)

Таким образом, получается, что для определения медленно меняющихся: процессов функцию смещения

(19.69)

следует подставить в уравнение автоматической системы (19.1) вместо заданной нелинейности Р (х, рх).

Следовательно, функция смещения Ф (х°) представляет собой как бы статическую характеристику (обычно криволинейную), которая определяет зависимость между выходной и входной величинами заданной нелинейности для постоянных или медленно меняющихся сигналов в автоколебательной системе.

При любых нелинейностях, в том числе и скачкообразных, функция смещения Ф(х°) может получать при определенных условиях вид весьма плавной кривой. Этот эффект называется вибрационным сглаживанием нелинейностей

при помощи автоколебаний, а функцию смещения Ф(х°) можно называть сглаженной нелинейной характеристикой.

Так, в примере § 19.1 согласно (19.40) функция смещения будет иметь вид рис. 19.6, а, т. е. для медленно меняющегося сигнала в данной релейной системе нелинейная характеристика будет в определенных пределах иметь плавный вид (рис. 19.6, а) вместо скачкообразного (рис. 19.6, 6) — за счет сглаживающего влияния автоколебательных вибраций.

Далее, например, для нелинейностей, обусловленных зоной нечувствительности (рис. 19.7, а), а также зазором (рис. 19.7, в) и петлей, сигналы х < b при отсутствии автоколебаний не передаются (F = 0). При наличии же автоколебаний сигнал х° < b передается в виде составляющей Р°. Поэтому для медленно меняющегося сигнала получается плавная характеристика (функция смещения) Ф (х°) без зоны нечувствительности (рис. 19.7, б). Эффект вибрационного сглаживания нелинейностей в этих примерах является положительным (ликвидация зон нечувствительности и петель). Однако в других случаях эффект вибрационного сглаживания нелинейности может оказаться и отрицательным. Возьмем, например, нелинейную характеристику с зоной насыщения (ограниченно-линейную), показанную на рис. 19.8; В этом случае за счет того, что верхушки синусоиды с одной стороны срезаются, постоянная составляющая F° будет меньше, чем само значение F, соответствующее линейному начальному участку. Поэтому

постоянный или медленно меняющийся сигнал будет при наличии автоколебаний проходить через данную нелинейность с меньшим коэффициентом усиления, чем без автоколебаний, что может в известных случаях отрицательно сказаться на качестве автоматической системы в целом.

Во многих случаях вычисление а и w будет необходимо только с точки зрения проверки выполнения условий вибрационного сглаживания нелинейности и допустимости таких вибраций в данной конкретной автоматической системе. Основными же для качества работы автоматической системы при этом будут являться медленно меняющиеся процессы, определяемые уравнением (19.68). С точки зрения упрощения их определения весьма важными являются следующие два обстоятельства.

Во-первых, вид функции смещения Ф (х°), как видно из § 19.1, не зависит ни от количества и места приложения внешних воздействий на систему, ни от характера их изменения (если только они медленно меняющиеся). Вид Ф (x°) зависит от формы нелинейности, от структуры и от параметров системы. Поэтому можно пользоваться любым методом определения Ф (х°) при любых частных упрощающих предположениях относительно внешних воздействий. Можно, например, пользоваться более простым вторым методом из описанных в § 19.1 методов и проиллюстрированных там на примере, взяв любое одно постоянное по величине внешнее воздействие.

Во-вторых, какова бы ни была заданная нелинейность F(х, рх) (скачкообразная, петлевая и т. п.), обычно функция смещения Ф (х°) получает вид плавной кривой. Поэтому, в отличие от первоначально заданной нелинейности, ее легко можно линеаризовать обычным способом (по касательной или но секущей в начале координат или в другом начале отсчета). Имея ввиду это свойство, часто вместо термина «вибрационное сглаживание» употребляют термин «вибрационная линеаризация» (будем придерживаться первого из них).

Итак, в определенном диапазоне можно считать

где

(19.70)

Графически kн представляет собой тангенс угла наклона прямой (касательной или секущей, рис. 19.7, б).

Величина коэффициента kн зависит от соотношения, вообще говоря, всех параметров системы.

Например, для системы, описываемой уравнениями (19.20) - (19.23), согласно (19.53) и (19.50) имеем

(19.71)

Поэтому для расчета медленно протекающих процессов в данной системе на основании (19.20) — (19.22) и (19.70) получаем линейные уравнения;

(19.72)

или единое линейное уравнение (19.24), в котором надо заменить х на х0 и F(х) на kнx0. Определение коэффициента усиления kн можно значительно упростить следующим образом. Поскольку (функция смещения Ф (х°) определяется согласно (19.13) и (19.7) по выражению F0(х°, а, w), в которое подставлена зависимость а (х°), то формулу для вычисления kн можно представить в виде

В тех случаях, когда рассматриваются нечетно-симметричные нелинейности F(х), величина F° не зависит от w и, кроме того, согласно (19.6)

так как производная под знаком интеграла будет четной функцией. Следовательно, для нечетно-симметричных нелинейностей F(х), как однозначных так и петлевых, величину kн можно вычислять по формуле

непосредственно из выражения (19.7), не определяя функции смещения Ф (х°), Во многих задачах это будет существенным упрощением решения.

Это упрощение не относится к несимметричным нелинейностям, а также к тем случаям, когда kн приходится определять не по касательной, а по секущей.

Итак, с подстановкой (19.70) уравнение (19.68) для определения медленна протекающих процессов становится обыкновенным линейным уравнением

(19.73)

я, как таковое, легко решается.

Как видим, введенный здесь принцип разделения уравнений для колебательных и для медленно меняющихся составляющих, при котором сохраняются существенно нелинейные свойства системы, приводит к весьма важным для практических расчетов результатам. Существенным выводом является то, что медленно меняющиеся сигналы проходят через нелинейность с другим коэффициентом усиления kн, чем автоколебания.

Особенно важно использовать свойство вибрационного сглаживания нелинейностей с последующей их обычной линеаризацией при расчете сложных автоматических систем.

Если, например, система автоматического управления полетом самолета работает по схеме, изображенной на рис. 19.9, то часть системы, обведенную пунктиром (релейный усилитель, привод и дополнительная обратная связь), как отдельную следящую систему, можно рассчитывать изложенным выше методом с учетом автоколебательных вибраций. Частоту последних путем соответствующего выбора параметров этой части системы или введением корректирующих устройств можно сделать достаточно большой с тем, чтобы амплитуда автоколебаний переменной х2 на выходе этой части системы была мала. Если же указанную амплитуду x2 не удается сделать малой (тогда руль будет колебаться), то необходимо, чтобы указанная частота практически не воспринималась корпусом самолета в процессе его движения вокруг центра тяжести.

Тогда расчет автоматической системы будет выглядеть следующим образом. Автоколебания определяем только в обведенной пунктиром внутренней части (рис. 19.9), как в отдельной самостоятельной системе, считая х5(t) произвольным медленно меняющимся внешним входным воздействием, а х2 — выходной величиной. Для такой простой системы находим, как изложено выше, функцию смещения Ф (х°), а также частоту и амплитуду автоколебаний в зависимости от величины внешнего воздействия. Выбираем параметры данной части системы так, чтобы условия вибрационного сглаживания нелинейности соблюдались во всем практически возможном диапазоне изменения входной величины х2. При этом следим за тем, чтобы частота автоколебаний системы (зависящая от параметров системы) лежала за пределами частот возможных колебаний самолета (чтобы она практически не воспринималась корпусом самолета). После такого расчета внутренней части системы производим обычную линеаризацию функции смещения Ф (х°), т. е. заменяем ее одной прямой линией F° = kнx0 (причем можно использовать указывавшееся упрощение в определении kн). В результате получаем линейное уравнение для медленно протекающих процессов в данной части системы. К этому уравнению добавляем уравнение всей остальной части системы (в данном случае самолета, чувствительных элементов и руля, см. рис. 19.9) и рассчитываем всю систему в целом, как линейную, по любым обычным методам теории автоматического регулирования. При этом не обращаем уже внимания на автоколебания, которые локализуются в рассчитанном ранее внутреннем контуре системы. Однако их влияние не игнорируется, ибо оно было учтено при определении функции смещения Ф (х°) и коэффициента kн.

Изложенный принцип позволяет, во-первых, вести расчет автоколебаний по более простым уравнениям (так как выделяется только внутренняя часть системы) и, во-вторых, значительно упрощает расчет всей системы в целом, сводя его к исследованию обыкновенных линейных уравнений (но с коэффициентом kн, зависящим от автоколебаний, т. е. от параметров внутреннего контура системы). Если необходимо учесть переменные коэффициенты и нелинейности самого самолета, то уравнения системы в целом не будут уже столь простыми. Однако и в этом случае полностью сохраняет смысл предварительный отдельный расчет внутреннего контура системы, так