Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

ГЛАВА 22 СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ

§ 22.1. Статистическая линеаризация нелинейностей

Предварительно заметим, что по уравнениям, выведенным в § 19.2 и в § 21.2, можно исследовать также медленно меняющиеся случайные процессы в автоматической системе, сопровождающиеся соответственно автоколебаниями и вынужденными колебаниями. При этом целесообразно функцию смещения Ф (x°) подвергнуть обычной линеаризации (19.70) и затем целиком применить линейную теорию случайных процессов к уравнению (19.73) или (21.44). Нелинейная же колебательная часть решения определяется с помощью гармонической линеаризации так же, как и в § 19.2 и в § 21.2. При этом находятся сглаженная характеристика (функция смещения) и зависимости амплитуды и частоты колебательной составляющей от величины медленно меняющейся составляющей. В этом случае предполагается, что внешние воздействия f(t) в (19.73) и f1 (t) в (21.44) являются медленно меняющимися случайными процессами с нормальным законом распределения (см. подробнее § 10.1 в книге [100]).

Для решения других задач при случайных воздействиях удобно бывает применять так называемую статистическую линеаризацию нелинейностей, разработанную И. Е. Казаковым [49]. Сущность ее заключается в следующем.

Для оценки динамической точности автоматических систем при случайных воздействиях будем определять два первых вероятностных момента случайных процессов; математическое ожидание (среднее значение) и дисперсию (или среднеквадратичное отклонение). Последнее эквивалентно определению спектральной плотности или корреляционной функции.

Если нелинейная система описывается дифференциальным уравнением

(22.1)

то схематически можно себе представить прохождение сигналов, как показано на рис. 22.1. Проходя через линейную часть, случайный процесс f(t), заданный двумя первыми вероятностными моментами, преобразуется в переменную х, которую тоже можно определить двумя первыми моментами. Однако определение дальнейшего преобразования случайного процесса х (t) в нелинейном звене F(х, рх) существенно связано с высшими вероятностными моментами (подобно тому как в главе 18 приходилось иметь дело с высшими гармониками). Ввиду замкнутости контура системы это обстоятельство накладывает отпечаток и на все процессы в данной системе. Поэтому точное решение задачи в большинстве случаев оказывается недоступным.

Достаточно хорошее для целей инженерных расчетов первое приближение применительно к рассматриваемым классам систем, обладающих свойством фильтра (см. § 18.2), дает пренебрежение высшими моментами, т. е. замена нелинейного звена эквивалентным линейным, которое одинаково с данным нелинейным преобразует два первых вероятностных момента; математическое ожидание (среднее значение) и дисперсию (или среднеквадратичное отклонение). Это и называется статистической линеаризацией нелинейности.

Эта операция по общей идее (но не по конкретному содержанию) аналогична тому, как в главе 19 нелинейное звено при помощи, гармонической линеаризации заменялось эквивалентным линейным, которое одинаково с данным нелинейным преобразует постоянную (или медленно меняющуюся) составляющую и первую гармонику колебательной составляющей, т. е. принимались во внимание два первых члена ряда Фурье и отбрасывались все высшие гармоники.

Итак, представим переменную х под знаком нелинейности F(х, рх) в виде

(22.2)

где х — математическое ожидание (среднее значение), которое является обычной (регулярной) функцией времени, и хсл —- случайная составляющая с нулевым математическим ожиданием (центрированная случайная функция времени). Это представление аналогично тому, которое употреблялось в главе 19 при гармонической линеаризации, но оно имеет совсем другой, вероятностный смысл. Далее, и переменную F(х, рх) также представим в виде

где F — математическое ожидание (среднее значение) нелинейной функции Р, которое является регулярной составляющей, xсл — эквивалентный коэффициент усиления случайной составляющей (центрированной). Это выражение по форме тоже аналогично тому, которое применялось в главе 19, но имеет иное конкретное содержание. Величина регулярной составляющей F определяется, следовательно, по известной

формуле для математического ожидания. В случае однозначной нелинейной функции F(х) эта формула дает

(22.4)

где М — обозначение операции взятия математического ожидания, w(х) — дифференциальный закон распределения случайной составляющей, например нормальный закон (рис. 11.10):

(22.5)

Для нелинейности общего вида F(х, рх) будет более сложное выражение:

(22.6)

которое для петлевых нелинейностей F(х) при симметричном законе распределения (в том числе и нормальном) упрощается. Например, для нелинейности, показанной на рис. 22.2, будет

(22.7)

Величину эквивалентного коэффициента усиления qсл случайной составляющей в формуле (22.3) рекомендуется определять одним из следующих двух способов.

Первый способ исходит непосредственно из величин среднеквадратичных отклонений σ x и σ F переменной х и нелинейной функции F, а именно:

(22.8)

что в случае однозначной нелинейности F(х) дает

(22.9)

Для общего случая F(х, рх) и в случае петлевой нелинейности F(х) получаются более сложные выражения, которые можно получить для qсл, обобщив (22.9) по тому же образцу, как обобщены выражения (22.6) и (22.7) по сравнению с (22.4).

Второй способ заключается в определении коэффициента qсл из условия минимума математического ожидания квадрата разности истинной нелинейной функции F(х, рх) и ее заменяющей (22.3), т. е. минимума среднеквадратичного отклонения. Записав это условие

получим

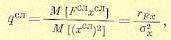(22.10)

где rFx — значение взаимной корреляционной функции переменных F и х при m= 0. Отсюда в случае однозначной нелинейности F(х) находим

Аналогично предыдущему легко получить также выражение коэффициента qсл для общего случая F(х, рх) и для петлевой нелинейности F(х).

Второй способ определения коэффициента qсл приводит к более простым расчетным формулам. С этой точки зрения его использование предпочтительнее. По точности же оба способа примерно равноценны и соответствуют общей степени приближенности всего метода в целом. Замечено, что во многих случаях, когда первый из этих способов дает завышенные значения корреляционной функции нелинейного процесса F(t) по сравнению с точными, второй дает заниженные значения. Поэтому часто может получиться более хорошее приближение, если в качестве величины qсл взять среднее арифметическое из двух: (22.8) и (22.10).

Важно иметь в виду, что величины F и qсл взаимосвязаны тем, что каждая из них зависит от обеих рассматриваемых характеристик случайного процесса: х и σ х (входящих в закон распределения w). Сам факт наличия этих зависимостей и их взаимосвязь и позволяют, несмотря на линеаризацию задачи, уловить существенно нелинейные особенности случайных процессов, подобно тому как в прежних главах зависимость величин Р°, q и q' от всех трех неизвестных х°, σ и w (или по крайней мере от первых двух из них) и

взаимосвязь этих величин позволяли исследовать существенно нелинейные особенности регулярных процессов во времени методом гармонической линеаризации.

Приведем выражения величин F и qсл и их графики для некоторых типовых нелинейностей, составленные по формулам (22.4), (22.9) и (22.11) при условии нормального закона распределения (22.5) случайной переменной х (при других законах распределения величины F и qсл имели бы другие выражения).

1. Идеальная релейная характеристика (рис. 22.3, а). Из формулы (22.4) находим

где обозначено

(22.12)

(числовые значения этого интеграла вероятностей имеются в некоторых сборниках математических таблиц). Зависимость величины F/с от отношения х/σ х показана графически на рис. 22.3, б.

По формулам (22.9) и (22.11) находим соответственно

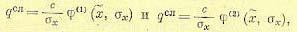(22.13)

где

Зависимости ф(1) и ф(2) показаны на рис. 22.3, в.

2. Однозначная релейная характеристика с зоной нечувствительности

(рис. 22.4, а). По формуле (22.4) с учетом обозначения (22.12) находим

где

(22.14)

Функция F/с изображена графически на рис. 22.4, б в зависимости от при разных значениях σ 1.

По формулам (22.9) и (22.11) получаем выражения типа (22.13), где

что изображено графически на рис. 22.4, в и г.

3. Петлевая релейная характеристика общего вида (рис. 22.5, а). По формулам

(22.7) находим где кроме (22.14) и (22.12) введены, еще обозначения

Зависимость F/с для случая m = 0,5 показана на рис. 22.5,6. Далее получаем выражения типа (22.13), где

Эти функции для случая m = 0,5 изображены на рис. 22.5, в и г.

4. Характеристика типа насыщения (рис. 22.6, а). По формуле (22.4) с учетом обозначений (22.12) и (22.14) находим

что показано в зависимости от x1 при разных σ 1 на рис. 22.6,6. По формулам же (22.9) и (22.11) находим выражение (22.13), где

что изображено на рис. 22.6, е и г.

§ 22.2. Простейшие случайные процессы в нелинейных системах

В данном параграфе рассматриваются такие задачи, в которых регулярная составляющая процесса х (математическое ожидание) постоянна или медленно меняется во времени по сравнению с составляющими основных частот спектра случайной составляющей хсл.

Обратимся к нелинейным системам, динамика которых описывается уравнениями вида

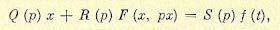(22.15)

где f(t) — внешнее воздействие, представляющее собой случайный процесс, причем

Здесь f — заданное математическое ожидание (регулярная составляющая), а fсл — центрированная случайная составляющая.

Пусть параметры системы таковы, что автоколебания отсутствуют и система устойчива относительно равновесного состояния. Применив статистическую линеаризацию (22.3) и подставив полученное выражение в заданное уравнение (22.15), разобьем последнее на два уравнения;

(22.18)

соответственно для регулярных (математических ожиданий) и случайных (центрированных) составляющих. При этом

определяются для каждой заданной нелинейности, как указано в §. 22.1 Рассмотрим в общем виде две различные задачи.

Первая задача. Если имеет место стационарный процесс, то величины f, х, σ х являются постоянными (имеет место некоторый установившийся режим) и уравнение (22.17) принимает алгебраический вид;

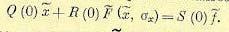(22.19)

Здесь фигурируют две неизвестные: х и σ х. Поэтому в принципе отсюда можно лишь выразить величину х как функцию σ x:

(22.20)

Далее по линейной теории случайных процессов, описанной в главе 11, производится исследование уравнения (22.18). В этом уравнении величина fсл задана спектральной плотностью sf(w) или корреляционной функцией rf(τ ). Линейная теория дает

(22.21)

где в выражении

(22.22)

необходимо х заменить найденной выше функцией (22.20). Тогда в уравнении (22.21) останется одна неизвестная величина σ х. Учитывая формулы (11.91) и (11.92), уравнение (22.21) можно записать в виде

(22.23)

где h — постоянный множитель, выносимый за знак интеграла (формулы для вычисления интеграла In приведены в приложении 2).

Таким образом, путем решения уравнения (22.23) с подстановкой (22.20) будет найдено среднеквадратичное отклонение σ х, а затем по формуле (22.20) будет вычислено и математическое ожидание х, т. е. полностью определится искомое приближенное решение уравнения (22.15):

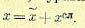(22.24)

Это решение справедливо для случая установившегося режима при стационарном случайном процессе.

Однако зависимость х (σ x) далеко не всегда можно выразить из уравнения (22.19) в явном виде ввиду сложности выражения F(х, σ х). Поэтому в большинстве случаев придется решать совместно два уравнения, (22.19) и (22.23), либо численно, путем последовательных приближений, либо графически.

Можно применять, например, следующий графический прием. Представим уравнение (22.19) в виде двух уравнений;

(22.25)

Первое из них дает прямую 1 (рис. 22.7, а), а второе — серию кривых 2 для различных постоянных значений σ х. Перенеся^все точки пересечения этих кривых с прямой 1 на плоскость координат х, σ х (рис. 22.7, б), получим зависимость σ х(х) в виде кривой 3, так как каждой точке пересечения :на верхнем графике соответствовало определенное значение ах. После этого построим (рис. 22.7, б) еще одну зависимость σ х(х) в виде кривой 4 по формуле (22.23), подставляя в правую часть этой формулы значения σ х, взятые для каждого х из кривой 3. Очевидно, что координаты точки пересечения С кривых 3 и 4 представляют собой искомый результат совместного решения уравнений (22.19) и (22.23).

Вторая задача. Перейдем теперь к решению другой задачи, когда исследуется неустановившийся процесс.

Часто в автоматических системах управления разложению искомого решения (22.24) на о: и хсл соответствует разложение его на полезный регулярный сигнал х и случайную помеху хсл. Когда полезный сигнал управления х изменяется во времени, процесс уже не будет стационарным. Однако, если помехи (флуктуации) характеризуются спектром значительно более высоких частот, чем полезный сигнал, можно считать последний медленно меняющимся. Тогда можно исследовать случайный процесс в первом приближении как стационарный, применяя формулу (22.23). Но при этом для определения регулярной составляющей х нельзя пользоваться алгебраическим уравнением (22.19), а надо обращаться к дифференциальному уравнению (22.17).

В этом случае описанное выше графическое решение не годится и следует поступать иначе. Сначала надо из уравнения (22.23) определить зависимость σ x (х). Для этого по аналогии с графическим решением (21.25) разобьем уравнение (22.23) на два уравнения;

(22.26)

Первое из них дает параболу 1 (рис. 22.8), а второе — серию кривых 2 при разных постоянных значениях х. Перенеся ординаты их точек пересечения на плоскость х, σ x и отложив для каждой из них соответствующие кривым 2 абсциссы х, получим в виде кривой 3 (рис. 22.8) искомую зависимость σ х (х).

Подставив полученную зависимость σ х (х) в вычисленное для заданной нелинейности согласно § 22.1 выражение

(22.27)

исключим из него величину σ х и получим функцию от одной переменной

(22.28)

которую, как и в главе 19 и § 21.2, можно назвать функцией смещения , так как здесь, математические ожидания х и F представляют собой смещения центра случайных составляющих.

Когда функция смещения (22.28) найдена, ее можно подставить в уравнение (22.17);

(22.29)

и отсюда по заданной функции f(t) найти путем решения дифференциального уравнения регулярную составляющую процесса х (t).

В большинстве задач функция смещения (22.28) будет иметь вид плавной кривой (рис. 22.9), которую в некоторых пределах можно подвергнуть обычной линеаризации

(22.30)

В случае, если система такова, что линейная часть с передаточной функцией

не пропускает спектр частот, соответствующий флуктуациям fсл (t) и определяемый спектральной плотностью sf(w), отыскание величины σ х значительно упрощается, а именно из (22.21) следует

(22.31)

т. е. σ х не будет зависеть от формы ,нелинейности и от величины х.

В этом случае вместо дифференцирования функции смещения (22.28) можно определить kн непосредственно 2) из (22.27);

Здесь kн получается как функция от σ x;

Затем надо подставить величину σ х, найденную из формулы (22.31).

Вместо этого можно воспользоваться кривой на рис. 22.3, б—22.6, б, соответствующей найденному значению σ x. При этом вычисление интеграла (22.31) производится по готовым формулам σ x2= hIп (см. приложение 2).

В результате подстановки (22.30) или (22.32) уравнение для определения регулярной составляющей (22.29) станет линейным;

(22.34)

Оно решается при помощи обычного характеристического уравнения

(22.35)

Важно отметить, однако, следующее. Согласно формулам (22.21) и (22.31) величина σ х зависит от спектральной плотности помехи sf(w). Поэтому и определяемая через величину σ x форма функции смещения (22.28) и крутизна ее (рис. 22.9) зависят не только от параметров самой системы, но также и от спектральной плотности помехи sf (w). Но если kн зависит от , то согласно (22.34) и (22.35) все статические и динамические качества и даже устойчивость системы по полезному сигналу будут зависеть не только от параметров самой системы, но и от параметров спектральной плотности внешней случайной помехи. Следовательно, устойчивая при отсутствии помех нелинейная система может при определенном уровне помех потерять свои качества, т. е. выйти из строя как система автоматического управления не по причине того, что система перестает фильтровать