Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

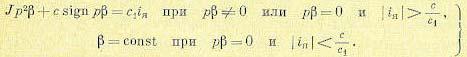(17.39)

При написании уравнения линейной части системы (16.53) пренебрежем постоянными

времени (чтобы иметь возможность рассматривать уравнение всей системы как уравнение второго порядка), а именно;

(17.40)

Подставив это в уравнения объекта (17.39) и обозначив

получим уравнение всей следящей системы в целом:

(17.41)

(17.42)

За координаты фазовой плоскости примем, как обычно, х = β , у = рβ . Условие у= 0 и

изображается на фазовой плоскости отрезком АВ (рис. 17.5).

Вне этого отрезка согласно (17.41) необходимо отдельно рассмотреть два случая:

y = pβ ≥ 0 и y = pβ ≤ 0 , т. е. верхнюю и нижнюю половины фазовой плоскости. При y ≤ 0 из (17.41) имеем

Это уравнение совпадает с уравнением (16.23), но со сдвигом на величину х= b1 . a2

Следовательно, ниже оси а; надо нанести такие же кривые, как на рис. 16.9, или как на рис. 16.11, б, но со сдвигом начала координат в точку А, что и сделано на рис. 17.5, а и б соответственно.

Аналогичные кривые наносятся и выше оси x, но только со сдвигом начала координат в точку В (рис. 17.5), так как согласно (17.41) при y > 0 имеем уравнение

В обоих случаях (рис. 17.5, а и б) система устойчива, причем в первом: случае переходный процесс состоит из конечного числа затухающих колебаний управляемого объекта, а во втором случае имеем апериодическое движение. Положение равновесия объекта определяется неоднозначно, объект может остановиться в любой точке особого отрезка АВ (рис. 17.5), как это было уже ранее при наличии зоны нечувствительности (см. пример

1). Особый отрезок АВ определяется соотношением | Мвр | =с1iя<с, где с — абсолютное значение момента сухого трения при движении управляемого объекта.

Заметим, что произведенное здесь упрощение уравнений системы хотя и позволило решить их точно, но это решение, дающее в результате устойчивость системы при любых числовых значениях параметров системы, неполно отражает действительную картину явлений в данной нелинейной системе.

Метод точечного преобразования. Как видно было из примеров, фазовая траектория обычно складывается из отдельных кусков, представляющих решение уравнений системы по участкам.

Пусть (рис. 17.6, а) граничными линиями между кусками фазовых траекторий являются ось х, линия FG и линия LN.

Возьмем начальное положение изображающей точки М0 где-нибудь на полуоси Ох. Один этап движения системы состоит в переходе изображающей точки на линию РО, ограничивающую этот этап, в некоторое положение М1 (рис, 17.6, а). Следующий этап переводит изображающую точку в положение М2 на полуоси ОН, затем в положение М3 на кривой LМ и, наконец, в положение М4 на исходной полуоси Ох.

Каждому положению М0 (х0, 0) на полуоси Ох соответствует определенное положение точки М1 (х1,y1) на кривой FG. Это называется точечным преобразованием полупрямой Ох в кривую FG. Для краткости ему присваивают название, например: преобразование S+. Дальше (рис. 17.6, а) идет точечное преобразование кривой FG в полупрямую ОН, названное Е+; затем — точечное преобразование S- полупрямой ОН в кривую LN и преобразование Е- кривой LN в исходную полуось Ох.

Все это в целом (или, как говорят, преобразование S+Е+S-Е-) называется точечным преобразованием полупрямой Ох самой в себя. Это преобразование в данном случае записывается в виде определенной зависимости:

где через x4 и х0 обозначены абсциссы точек M4 и М0 (рис. 17.6, а). Если при любом х0 оказывается x4 < х0, то в системе будет затухающий процесс, а если x4 > х0 — расходящийся процесс. Если же возможно равенство ,х4=х0, то на фазовой плоскости получится предельный цикл, который, как известно, может изображать либо устойчивый автоколебательный процесс, либо границу устойчивости системы в малом, либо может соответствовать особому случаю бифуркации (см. ниже).

Втех случаях, когда общая картина фазовых траекторий разделяется на две симметричные части, достаточно исследовать только половину всего точечного преобразования.

Врассматриваемом случае верхняя полуплоскость симметрична нижней относительно

начала координат. Поэтому достаточно рассмотреть только первую половину преобразования (S+Е+), т. е. точечное преобразование Ох в полупрямую ОН, и выразить его в виде зависимости

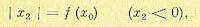(17.43)

причем условие наличия предельного цикла на фазовой плоскости будет |x2| = х0 при х2<0. Пусть, например, зависимость (17.43) имеет вид кривой, показанной на рис. 17.6, б. Проведем на этом графике еще прямую из начала координат под углом 45° к

Заметим, что изложенное выше является лишь качественным рассмотрением, так как в нем отсутствует время t. Остается неизвестным течение процессов во времени, период (частота) автоколебаний. Чтобы получить полное решение задачи, нужно к данному рассмотрению добавить еще решение дифференциальных уравнений на отдельных участках во времени (как в методе припасовывания, см. § 16.1). Поэтому в методе точечного преобразования вводится соответствующий временной параметр (здесь это не рассматривается).

Для систем выше второго порядка вместо фазовой плоскости придется иметь дело с фазовым пространством и с точечным преобразованием не линий, а поверхностей. Там появляются новые особенности процессов. Однако ввиду чрезвычайной сложности таких построений рассматривать их не будем.

Метод изоклин. Выше были рассмотрены такие примеры нелинейных систем второго порядка, для которых фазовые траектории легко находятся интегрированием уравнений по участкам. В тех случаях, когда интегрирование затруднено, ход фазовых траекторий, хотя бы качественно, можно проследить с помощью так называемого метода изоклин (без интегрирования уравнений). Количественно этот способ имеет сравнительно низкую точность. Применение его; пока ограничено системами второго порядка.

Изоклиной называется такая линия, во всех точках пересечения которой с фазовыми траекториями последние наклонены под одним и тем же определенным углом к оси абсцисс х. Так, если известно дифференциальное уравнение фазовых траекторий

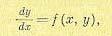(17.44)

то для получения изоклины нужно положить

Уравнение изоклины, следовательно, будет

(17.45)

где с обозначает определенный тангенс угла наклона фазовых траекторий. Каждому заданному значению с соответствует своя изоклина. Например, часто встречается нелинейное уравнение

которое можно записать в виде

тогда дифференциальное уравнение фазовых траекторий будет выглядеть так:

а уравнение изоклин

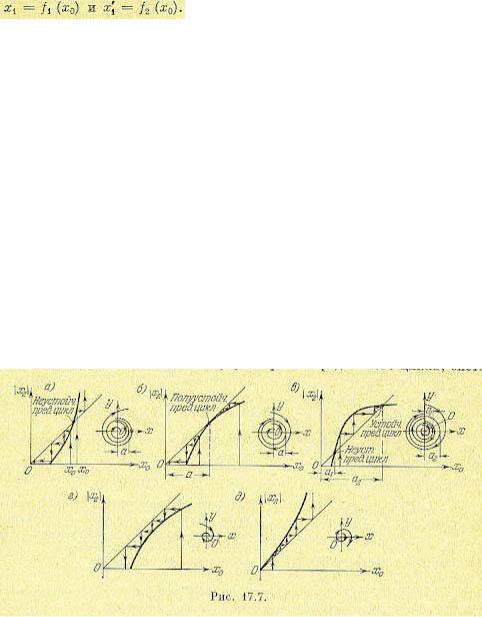
Задавая различные значения с (при заданном К), для каждого из них строим по этому уравнению кривую на фазовой плоскости — изоклину (сплошные кривые на рис. 17.8).

Затем на каждой кривой наносим стрелочки под углами а = arctgс к оси абсцисс (на рис. 17.8 указаны значения с для каждой кривой). Из этих стрелочек и составляются искомые фазовые траектории; некоторые из них изображены на рис. 17.8 пунктиром. В данном случае получается устойчивый предельный цикл, что соответствует автоколебаниям в системе.

§ 17.2. Теоремы прямого метода Ляпунова и их применение

Предварительно заметим, что при изложении прямого метода Ляпунова,, именуемого также второй методой Ляпунова, будем пользоваться дифференциальными уравнениями автоматической системы в форме уравнений первого порядка, полагая, что они записаны для переходного процесса в отклонениях всех переменных от их значений в установившемся процессе при новых постоянных значениях возмущающего f = f° и задающего g = g° воздействий. Следовательно, эти уравнения для нелинейной системы n- го порядка будут:

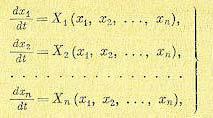(17.46)

где функции Х1, Х2, . . ., Хn произвольны и содержат любого вида нелинейности, но всегда удовлетворяют условию

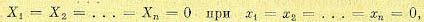(17.47)

так как в установившемся состоянии все отклонения переменных и их производные равны, очевидно, нулю по самому определению понятия этих отклонений.

Нам понадобятся в дальнейшем еще следующие сведения.

Понятие о знакоопределенных знакопостоянных и знакопеременных функциях.

Пусть имеется функция нескольких переменных

Представим себе n-мерное фазовое пространство (см. § 16.1), в котором xI, х2, . . ., хn являются прямоугольными координатами (это будут, в частности, фазовая плоскость при n = 2 и обычное трехмерное пространство при n = 3). Тогда в каждой точке указанного пространства функция V будет иметь некоторое определенное значение. Нам понадобятся в дальнейшем функции V (х1, х2, . . ., хn), которые обращаются в нуль в начале координат (т. е. при х1 = х2 = . . . = хn = 0) и непрерывны в некоторой области вокруг него.

Функция V называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат.

Функция V называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

Функция V называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

Приведем примеры всех трех типов функций V. Пусть n= 2 и V = x12 + x22 . Это будет

знакоопределенная (положительная) функция, так как V=0 только тогда, когда одновременно х1 = 0 и х2 = 0, и V > 0 при всех вещественных значениях x1 и х2.

Аналогично при любом n функция V = x12 + x22 +... + xn2 будет знакоопределенной

Если взять функцию V = x12 + x22 при n = 3, то она уже не будет знакоопределенной, так

как, оставаясь положительной при любых x1х2 и х3, она может обращаться в нуль не только при х1 = х2 = х3 = 0, но также и при любом значении х3, если x1= х2 = 0 (т. е. на всей оси х3, рис. 17.9, а). Следовательно, это будет знакопостоянная (положительная) функция. Наконец, функция V = x1 + х2 будет знакопеременной, так как она положительна для всех точек плоскости справа от прямой х1 = —х2 (рис. 17.9, б) и отрицательна слева от этой прямой.

Заметим, что в некоторых частных задачах нам понадобится также функция V, которая обращается в нуль не в начале координат, а на заданном конечном отрезке АВ (рис.17.9, б). Тогда знакоопределенность функции V будет обозначать ее неизменный знак и необращение в нуль в некоторой области вокруг этого отрезка.

Функция Ляпунова и ее производная по времени. Любую функцию

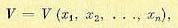(17.48)

тождественно обращающуюся в нуль при х1 = х2 = . . . = хn =0, будем называть функцией Ляпунова, если в ней в качестве величин х1, х2, . . ., хn взяты те отклонения переменных системы регулирования в переходном процессе

в которых записываются уравнения (17.46) для этой системы. Производная от функции Ляпунова (17.48) по времени будет

Подставив сюда значения dxdt1 ,..., dxdtn из заданных уравнений системы

регулирования в общем случае (17.46), получим производную от функции Ляпунова по времени в виде

(17.49)

где Х1, Х2, …, Хn — правые части уравнений (17.46) системы автоматического регулирования, представляющие собой заданные функции от отклонений x1, x2, . . ., хn. Следовательно, производная от функции Ляпунова по времени, так же как и сама V, является некоторой функцией отклонений, т. е.

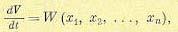(17.50)

причем согласно свойству (17.47) эта функция, W так же как и сама V, тождественно обращается в нуль при х1= х2 = . . . = хn = 0. Поэтому к ней в одинаковой степени можно применять все те же понятия знакоопределенности, знакопостоянства и

знакопеременности в некоторой области вокруг начала координат, о которых говорилось выше по отношению к функции V.

Здесь шла речь только об уравнениях (нелинейных), в которые не входит в явном виде время г, так как только этот случай будет рассматриваться в дальнейшем. Вообще же метод Ляпунова может применяться и при наличии времени t в явном виде, в частности для уравнений с переменными коэффициентами (линейных и нелинейных). Базируясь на этих предварительных сведениях, дадим общую формулировку теорем Ляпунова об устойчивости и неустойчивости нелинейных систем и покажем их справедливость. Теоремы эти годятся для исследования устойчивости систем регулирования не только при малых, но и при больших отклонениях, если для них

справедливы исходные уравнения данной системы регулирования. Устойчивость системы при любых больших начальных отклонениях называется коротко устойчивостью в целом.

Теорема Ляпунова об устойчивости нелинейных систем. Теорема формулируется следующим образом: если при заданных в форме (17.46) уравнениях системы n-го порядка можно подобрать такую знапоопределенную функцию Ляпунова V(x1 x2, . . ., хn), чтобы ее производная по времени W(х1, х2, . . . . . ., хn) тоже была знакоопределенной (или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива. При знакоопределенной функции W будет иметь место асимптотическая устойчивость.

Проиллюстрируем справедливость этой теоремы на наглядных геометрических образах. Для простоты возьмем систему третьего порядка (n = 3). Уравнения (17.46) для нее в общем виде будут

(17.51)

Возьмем знакоопределенную положительную функцию Ляпунова в виде

(17.52)

где а, b, с — произвольно заданные вещественные числа. Будем придавать величине V возрастающие постоянные значения: V = 0, С1, С2, С3, . . ., что означает

Первое из этих выражений соответствует одной точке x1 = x2 = x3 = 0 (началу координат фазового пространства), а остальные — поверхностям эллипсоидов в фазовом пространстве, причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий (рис. 17.10).

Возьмем теперь производную от функции Ляпунова по времени. Согласно (17.49) и (17.52):

где функции Х1, Х2, Х3 берутся из заданных уравнений системы регулирования (17.51). Если полученная таким путем функция W(x1; х2, х3) окажется знакоопределенной отрицательной, т. е. если

(17.53)

во всех точках исследуемого фазового пространства, кроме одного только начала координат, где

то при любых начальных условиях изображающая точка М (рис. 17.10) вследствие (17.53) будет двигаться в сторону уменьшения значения V, т. е. будет пересекать эллипсоиды, изображенные на рис. 17.10, извне внутрь. В результате с течением времени изображающая точка М будет стремиться к началу координат О фазового пространства и уже никак не сможет выйти за пределы тех эллипсоидов, в которые она проникла.

Это и означает затухание всех отклонений х1,х2, х3 в переходном процессе с течением времени. Таким образом, установлена устойчивость данной системы регулирования, что иллюстрирует справедливость теоремы для системы третьего порядка (в случае знакоопределенной функции W).

Отсюда вытекает справедливость теоремы и в общем случае. Рассуждения остаются аналогичными, только вместо трех уравнений (17.51) будет n уравнений (17.46). Как и раньше, для любой знакоопределенной положительной функции Ляпунова V (х1, х2, . . ., хn) — С получим некоторые замкнутые поверхности, окружающие начало координат (рис. 17.10), но уже не в обычном трехмерном, а в n-мерном фазовом пространстве (их иногда называют гиперповерхностями). Поэтому, если производная

окажется знакоопределенной отрицательной, то траектория изображающей точки М в n- мерном пространстве при любых начальных условиях с течением времени будет пересекать указанные поверхности только извне внутрь, что и свидетельствует об устойчивости данной системы.

Если же функция W будет не знакоопределенной, а знакопостоянной, то очевидно, что траектория изображающей точки М не везде будет пересекать поверхности V = С а может их касаться в тех точках, где W обращается в нуль (помимо начала координат). Но так как во всех других местах фазового пространства функция W имеет один и тот же знак, вследствие чего изображающая точка может идти только извне внутрь поверхности V = С, то при решении задачи остается только проверить, не «застрянет» ли изображающая точка там, где W=0 (см. пример ниже).

Замечания к теореме Ляпунова об устойчивости. По поводу сформулированной теоремы Ляпунова об устойчивости системы необходимо сделать следующие два важных замечания.

1. В теореме речь идет о подборе функции Ляпунова V (x1 х2, . . ., хn). Вообще говоря, при заданных в форме (17.46) уравнениях системы регулирования можно подобрать несколько различных вариантов функции V, поскольку требуется только знакоопределенность ее и ее производной. Различные варианты функции V, удовлетворяющие теореме, могут дать соответственно различные варианты условий устойчивости для одной и той же системы регулирования. При этом одни из них будут шире, другие уже, последние могут входить в первые как частный случай и т. д. Поэтому, вообще говоря, данная теорема Ляпунова обеспечивает получение достаточных условий устойчивости, которые не всегда будут и необходимыми, т. е. при выполнении условий теоремы система наверняка будет устойчивой, но эти условия могут не

охватывать всей области устойчивости системы по параметрам. В самом деле, если выбрана функция V, удовлетворяющая теореме, нет уверенности в том, что нельзя подобрать другой вариант функции V, который бы еще более полно охватывал область устойчивости данной системы.

Геометрически это значит, что, получив определенное семейство поверхностей V=С (рис. 17.10) и убедившись, что траектории изображающей точки М приближаются к началу координат, пересекая эти поверхности извне внутрь, нельзя быть уверенным в том, что не существует еще других вариантов траекторий изображающей точки М, которые в отдельных местах могут пересекать данные поверхности изнутри вовне, но все же с течением времени в конце концов неограниченно приближаться к началу координат. Такие траектории будут соответствовать другому семейству поверхностей V = С, т. е. другому варианту выбора функции Ляпунова.

Вряде технических задач можно вполне удовлетвориться этими достаточными условиями устойчивости. От более или менее удачного подбора функции Ляпунова V будет зависеть большая или меньшая близость полученных достаточных условий устойчивости к необходимым и достаточным, т. е. более или менее полный охват всей области устойчивости данной системы. Существуют, конечно, и такие функций V (х1, х2, . . ., хn), которые соответствуют всей области устойчивости.

2. К сформулированной выше теореме Ляпунова необходимо добавить, что понятие устойчивости по Ляпунову допускает, чтобы при знакоопределенной функции V производная от нее W была не обязательно знакоопределенной или знакопостоянной, а могла быть и тождественно равна нулю во всем рассматриваемом фазовом пространстве.

Вэтом случае, проводя аналогичные прежним рассуждения, легко убедиться, что изображающая точка М (рис. 17.10) будет оставаться все время на какой-нибудь одной из поверхностей V = const, куда ее забросили начальные условия. В результате система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него.

Теорема Ляпунова о неустойчивости нелинейных систем. Поскольку предыдущая теорема Ляпунова дает, вообще говоря, только достаточные условия устойчивости и поскольку кроме области устойчивости нелинейная система может иметь целый ряд особых областей (см. § 16.1), то может возникнуть потребность в отдельном определении области неустойчивости путем использования нижеследующей теоремы Ляпунова, которая дает достаточные условия неустойчивости системы.

Теорема формулируется так: если при заданных в форме (17.46) уравнениях системы п-го порядка производная W(x1, х2, . . ., хn) от какой-нибудь функции Ляпунова V (х1, x2, . . ., хn) окажется знакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива.

Справедливость этой теоремы иллюстрируется геометрически следующим образом. Пусть для какой-нибудь заданной системы второго порядка (n = 2) найдена такая знакопеременная функция V(х1,х2), для которой производная

оказалась знакоопределенной положительной. Пусть при этом линии V (х1, х2) на фазовой плоскости располагаются, как указано на рис. 17.11, где линии АВ и СD соответствуют значениям V = 0 и разделяют те области, внутри которых V>0 и V<0.

то изображающая точка М с течением времени будет двигаться и пересекать линии V=С, переходя от меньших значений С к большим. Она может при этом лишь временно приблизиться к началу координат, но в конце концов будет неограниченно удаляться от начала координат. Это соответствует расходящемуся процессу, т. е. неустойчивости системы. Аналогично можно показать справедливость теоремы и для системы любого порядка n, проводя те же рассуждения для n-мерного фазового пространства.

Наиболее полно решение нелинейных задач теории регулирования с применением указанных теорем дано в известной книге А. И. Лурье [81], где предложено брать функцию Ляпунова в виде «квадратичная форма плюс интеграл» (см. также [98]). Приведем два примера применения изложенных теорем Ляпунова к исследованию нелинейных систем автоматического регулирования.

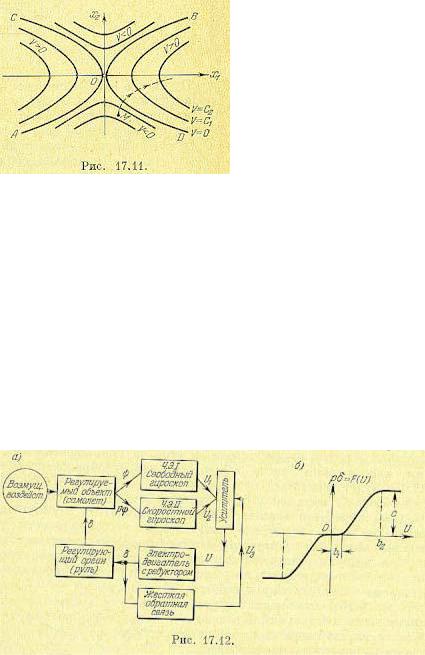
Пример учета нелинейности привода регулирующего органа. Такой пример применительно к системе самолета с курсовым автопилотом (в упрощенном виде) был рассмотрен в работе А. И. Лурье и В. Н. Постникова. Схема данной системы автоматического регулирования представлена на рис. 17.12, а.

Пусть все звенья системы являются линейными, за исключением электродвигателя (с редуктором), для которого будем рассматривать его реальную характеристику (рис. 17.12, б). Она может иметь произвольное криволинейное очертание с зоной застоя (при |U| <b1) и с зоной насыщения (при |U| >b2). Наклон характеристики и ее криволинейность могут быть любыми, лишь бы только соблюдались условия

(17.54)

Требуется найти условия устойчивости данной системы автоматического регулирования.

Уравнение самолета как регулируемого объекта в грубо упрощенном виде будет

(17.55)

где ψ — отклонение курсового угла самолета, δ — отклонение руля. Уравнения чувствительных элементов (гироскопов с потенциометрами):

(17.56)

Уравнение обратной связи