Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

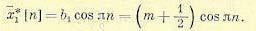(24.109)

Нормированный коэффициент гармонической линеаризации

(24.110)

В точке пересечения двух годографов (рис. 24.24, а) имеем — Z* =W (e jπ ) =W * ( j∞) . Так как W * ( j∞) ≤ MM+1 то получаем

(24.111)

откуда

(24.112)

Так как ∆1 >0, то при M<2 из последнего равенства следует, что m= 0, а дробная часть относительной амплитуды колебаний

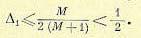(24.113)

Квазипериодические режимы. Если установившееся значение сигнала на выходе входного преобразователя должно соответствовать точке 3 на рис. 24.21, а, то в системе будет существовать несимметричный периодический режим.

Установившееся значение на выходе преобразователя можно представить в виде

(24.114)

где m — целое число, а x0 * —дробная часть, причем x0 * ≤1и∆ ≤1/ 2 .

Так как на самом деле на выходе может существовать сигнал m + 1 или m, то требуемое значение х0 получается как среднее значение в периодическом режиме. Как среднее в колебательном режиме получается и значение дробной части

(24.115)

где N1 — число тактов, когда на выходе существует величина m+ 1, N2 — число тактов, когда на выходе существует величина т, а 2N — число тактов полного периода колебаний.

Из (24.115), учитывая, что N1 + N2 = 2N, можно найти следующую зависимость:

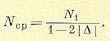(24.116)

Знак модуля введен в (24.116) для обобщения на случай произвольного знака ∆. Вместо N в формуле (24.116) записан средний полупериод Ncр по следующим соображениям. Числа N1, N2 и N могут быть в каждом реальном цикле колебаний только целыми, а ∆ — произвольное число. Поэтому зависимость (24.115) может, как правило, кроме специально подобранных значений ∆, выполняться только в среднем. Так, например, для случая, когда N1 = 1, некоторые подобные режимы изображены на рис. 24.25.

В формулах (24.115) и (24.116) числа N1, N2 и N могут быть целыми, вообще говоря, для любых значений ∆, если под N1 и N2 понимать число тактов не в одном цикле колебаний, а в течение многих циклов. Однако при этом все эти числа могут стремиться к бесконечности или во всяком случае быть очень большими. Период колебаний То = 2NТ в этом случае не соответствует реально наблюдаемым колебаниям в системе, у которых будет существовать некоторая преобладающая гармоника. Целью введения усредненного периода и является выявление частоты преобладающей гармоники.

Средний полупериод Nср может быть как целым, так и дробным числом. Средние значения чисел N1 и N2 могут быть также целыми и дробными. Такой режим движения будем называть квазипериодическим.

Проблема расчета квазипериодических режимов является весьма сложной. Поэтому ограничимся распространенным случаем, когда N1 = 1 не в среднем, а в течение всего режима. Тогда формулы (24.115) и (24.116) приобретают вид

(24.117)

(24.118)

Рассмотрим вначале случай, когда Nср = N — целое число. Для дробных частей х* и х* по-прежнему имеют место зависимости вида (24.81) и (24.82), а также рис. 24.21, б. Однако комплексное значение амплитуды первой гармоники b1 на выходе входного преобразователя определяется при N>1 более общим выражением:

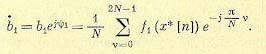(24.119)

Это выражение можно упростить, если учесть, что

f1 =1/ 2 + ∆ приυ = 0 и f1 = −(1/ 2 − ∆) при всех остальных значениях υ . Тогда

(24.120)

− j π υ

так как сумма членов вида e N к при υ = 0, 1, ..., 2N—1 равна нулю. Из (24.120) получается нормированный коэффициент гармонической линеаризации

(24.121)

Расчет параметров периодического режима, когда Nср = N — целое число, не

представляет труда. По значению ошибки в установившемся режима определяется относительный полупериод колебаний N (24.118) из (24.76) находится амплитуда колебаний на выходе системы:

(24.122)

где λN определяется формулой (24.106). На рис. 24.26 показано графическое

построение для N = 2.

Если Nср представляет собой дробное число, то колебания носят квазипериодический характер. Их приближенный расчет может быть сделан следующими методами.

1)Введем предположение, что при переходе от одного периодического режима с

целым значением N = N0 к другому с новым целым значением N = N0 + 1 амплитуда первой гармоники и частота усредненного периодического режима изменяются непрерывно и плавно. В части частоты колебаний это полностью подтверждается формулой (24.116). Тогда для расчета амплитуды первой гармоники колебаний можно воспользоваться тем же графическим построением (рис. 24.26) и формулами (24.116) и (24.122) при замене в последней N на Nср и w на w0.

2)Второй метод заключается в том, что для усредненного значения х[n], изображенного на рис. 24.27, а с учетом действия экстраполятора (пунктирная линия), находится обычными приемами разложения в ряд Фурье амплитуда первой гармоники

(24.123)

Далее может быть определена амплитуда колебаний на выходе системы пересчетом с1 на вход (умножением на δ1 ) и умножением на модуль частотной передаточной функции разомкнутой системы:

(24.124)

Здесь

(24.125)

— круговая частота и псевдочастота периодического режима (частота преобладающей гармоники).

3) Возможно использование способа расчета, когда рассматривается некоторый дополнительный усредненный режим движения у* (t) на выходе непрерывной части (рис. 24.27, б), полученный припасовыванием на интервалах времени 0 - Т и Т - Т0 = 2NcpТ. Далее в случае необходимости можно выделить в этом режиме первую гармонику. В отличие от предыдущих двух методов, здесь расчет может производиться и в тех случаях, когда время существования на выходе экстраполятора сигнала (m + 1)δ1 не подчиняется

условию N1 = 1, а может содержать произвольное число тактов.

Пример. Пусть передаточная функция непрерывной части

(24.126)

Дискретная частотная передаточная функция разомкнутой системы

(24.127)

где k = k0kц — общий коэффициент усиления разомкнутой цепи с присоединенным коэффициентом передачи ЦВМ (24.73).

Режим симметричных колебаний при х* = 0,5δ построен на рис. 24.28, а. Амплитуда может быть найдена методом припасовывания:

(24.128)

Так как из условий устойчивости КТ <2, то A<0,5δ . Относительный полупериод N=1. Первая гармоника этого колебательного режима .имеет амплитуду

(24.129)

Первая гармоника может быть также найдена из (24.103) для w0T = π и λ → ∞:

(24.130)

что близко совпадает с (24.129).

Рассмотрим теперь несимметричные колебания. Зависимость Nср от установившегося значения ошибки х0 в соответствии с (24.114) и (24.118) представлена на рис. 24.29. Точками отмечены целочисленные значения Nср.

Воспользуемся первым изложенным методом. В соответствии с (24.122)

(24.131)

При Nсp>2 формула (24.131) дает

(24.132)

При использовании второго метода в соответствии с (24.124)

(24.133)

При N >2 формула (24.133) переходит в (24.132).

Для того чтобы воспользоваться третьим методом, рассмотрим «средний» цикл колебаний. Он построен методом припасовывания для выходной величины на рис.24.28, б.

Амплитуда колебаний

(24.134)

Амплитуда первой гармоники при разложении в ряд Фурье

(24.135)

полностью совпадает со значением (24.131).

Все полученные выражения для амплитуды первой гармоники показывают сравнительное постоянство ее для различных значений Ncp.

ГЛАВА 25 АДАПТИВНЫЕ СИСТЕМЫ

§ 25.1. Системы экстремального регулирования

Системами экстремального регулирования называются системы, в которых задающие воздействия, т. е. заданные значения регулируемых величин, определяются автоматически в соответствии с экстремумом (максимумом или минимумом) некоторой функции F(y1, y2, y3, . . ., уn). Эта функция зависит не только от регулируемых величин у1, . . ., уn, но и от неконтролируемых параметров системы и времени г. Поэтому она не является постоянной и заранее известной. Однако изменение функции F и смещение экстремальных значений регулируемых величин уг = y1э, y2 = y2э, . . ., уn = уnэ протекает относительно медленно. Условием экстремума дифференцируемой функции нескольких переменных F(y1, y2, . . ., yn) является равенство нулю в точке экстремума частных производных этой функции;

(25.1)

Градиентом функции F называется векторная величина

(25.2)

где К1, . . ., Кn — единичные векторы осей, по которым отсчитываются величины y1, ...,yn В точке экстремума градиент равен нулю:

grad F=0 (25.3)

Задача поиска экстремума разбивается на две;

1)определение градиента;

2)организация движения в точке экстремума.

Для решения, как первой, так и второй задачи предложено много способов. Ниже будут рассмотрены только простейшие из них [61]. Обратимся сначала к задаче определения градиента.

Способ синхронного детектирования. Способ основан на том, что к основным медленно меняющимся величинам y1, . . ., уn добавляются малые гармонические (в общем случае периодические) составляющие;

(25.4)

Величина F(y1, . . ., уn) поступает на синхронные детекторы (рис. 25.1), у которых в качестве опорных величин используются те же переменные составляющие (25.4).

Идеальные синхронные детекторы умножают величину F на переключающую функцию, представляющую собой прямоугольную волну с периодом Тi= 2π /wi (i = 1, 2, . . ., n) и высотой единица. Переключающая функция приближенно может быть заменена синусоидой частоты wi с единичной амплитудой. Поэтому средние значения выходных величин синхронных детекторов u1,…,un могут быть приближенно представлены в

виде u1 = F sin w1t, u2 = F sin w2t,..., un = F sin wn t.

В квазистационарном режиме, когда составляющие y10 меняются медленно по сравнению с поисковым движением Аi sin wit, величины u1, . . ., un с точностью до малых высших

порядков пропорциональны соответствующим частным производным dF ,..., dF в точке dy1 dyn

y1 = y10 , y2 = y20 ,..., yn = yn0 .и, следовательно, определяют grad F в этой точке. Для доказательства этого разложим функцию F в окрестностях точки y10 ,..., yn0 в

Выходные величины синхронных детекторов можно представить в виде

(25.6)

Если величины y10 ,..., yn0 постоянны или меняются настолько медленно, что их изменениями за небольшой период можно пренебречь, то, учитывая очевидные равенства:

(25.7)

выражение (25,6) можно свести к виду

(25,8)

Погрешность метода определяется членом ∆uq , которому соответствует выражение

(25.9)

Величина ∆uq по отношению к амплитудам А1, . . ., Ат имеет порядок малости не ниже третьего, а по сравнению с uq — не ниже второго. Если частоты выбраны по закону нечетных чисел wi = (2i +1)w0 , где w0 = const то удовлетворяются условия wi ≠ wk (i ≠ k)

и wi ± wk ≠ wq .

Тогда

(25.10)

и величина ∆uq имеет порядок малости не ниже четвертого.

Следовательно, производная функции F по времени сохраняет свой знак (больше нуля при k >0 и меньше нуля при k<0) повсюду, кроме точки экстремума, где эта производная обращается в нуль, что соответствует монотонному сходящемуся процессу.

При шаговом движении реализуются зависимости

(25.15)

где ∆y1 , . . ., ∆yn — фиксированные шаги в направлении экстремума.

Для способа градиента характерно плавное движение по направлению к точке экстремума и малый размах колебаний около точки экстремума при шаговом движении.

Способ наискорейшего спуска. При способе наискорейшего спуска движение происходит по начальному направлению вектора градиента F до тех пор, пока производная функции F по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого вектора до обращения в нуль производной от F по этому направлению. Процесс повторяется до достижения точки экстремума.

Этот способ характеризуется быстрым выходом системы в район экстремума, что делает его предпочтительным для начальной стадии движения. В районе экстремума можно использовать другие способы, например способ градиента.

На рис. 25.2 для случая двух регулируемых величин, что соответствует F= F(у1, у2), изображены траектории движения для рассмотренных выше способов поиска экстремума [61]. Кривая 1 соответствует способу Гаусса — Зайделя, кривая 2 — способу градиента и кривая 3 — способу наискорейшего спуска.

Рассмотрим теперь пример экстремальной системы для наиболее простого случая, когда

F= F(у).

Пример. На рис. 25.3 изображена схема экстремального регулирования настройки колебательного контура. Полезный сигнал с частотой f поступает на параллельный резонансный контур, состоящий из катушки L и конденсаторов переменной емкости С1 и С2. Конденсатор С2 имеет сравнительно небольшую емкость. Ротор его вращается двигателем Д2 с постоянной скоростью, вызывая периодические изменения общей емкости контура, которая является регулируемой величиной.

Общая емкость колебательного контура

C = C1 + C2 = C1 +C20 + Asin w1t