Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

Ключи, изображенные на структурной схеме (рис. 24.4), генерируют импульсные функции в соответствии с периодом повторения ЦВМ. Проходя через запоминающее устройство (24.12), последовательность импульсных функций образует ступенчатую функцию (рис. 24.3).

Рассмотрим теперь простейшие примеры.

Пример 1. Пусть непрерывная часть системы регулирования соответствует астатизму первого порядка и представляет собой идеальное интегрирующее звено с передаточной функцией

В соответствии с (24.7) получаем дискретную передаточную функцию разомкнутой системы

(24.13)

Определим условие устойчивости замкнутой системы. Характеристическое уравнение системы 1+W(z) = 0 приобретает вид

Для выполнения условия | zi | < 1 необходимо, чтобы удовлетворялось неравенство

(24.14)

Это и будет условием устойчивости системы.

Если необходимо иметь запас устойчивости, то можно воспользоваться для его оценки, например, понятием показателя колебательности. Найдем дискретную частотную передаточную функцию, положив z= еjwT. В результате получаем

Нетрудно видеть, что амплитудно-фазовая характеристика представляет собой прямую, параллельную оси мнимых (рис. 24.5). Условие получения заданного показателя колебательности

(24.15)

Это условие дает допустимое соотношение между общим коэффициентом усиления К, который в рассматриваемом случае, как нетрудно показать,

равен добротности по скорости КΩ, и периодом повторения ЦВМ.

Построим переходный процесс при подаче на вход ступенчатого воздействия g(t)=1(t). Дискретная передаточная функция замкнутой системы

(24.16)

Изображение единичной ступенчатой функции будет (табл. 15.1)

(24.17)

Изображение выходной величины

(24.18)

Примем следующие значения произведения добротности по скорости на период повторения:

1) КТ = 1,4, что соответствует М = 1,5;

2)КТ = 1, что соответствует М = 1 для максимального значения КТ,

3)KТ = 0,5, что соответствует М = 1.

Раскладывая (24.18) в ряд Лорана, получаем значения выходной величины у [nТ] в дискретные моменты времени, соответствующие n = 0, 1, 2, . . . Процессы изображены на рис. 24.6. Значения выходной величины в дискретные моменты времени соединены между собой прямыми линиями, соответствующими переходным характеристикам интегрирующего звена, которым является непрерывная часть системы.

Нетрудно заметить, что оптимальный процесс будет при М = 1 (случай 2). Тогда переходный процесс длится конечное время, равное одному периоду повторения.

Пример 2. Рассмотрим систему с астатизмом второго порядка. Пусть передаточная функция непрерывной части имеет вид

В соответствии с (24.9) получаем

(24.19)

Воспользуемся для расчета методом логарифмических частотных характеристик. Для этой цели применим подстановку (15.162) и перейдем к w-преобразованию

(24.20)

Для перехода к частотной передаточной функции сделаем подстановку w = j T2 λ ,

где λ представляет собой абсолютную псевдочастоту. В результате получим частотную передаточную функцию

Модуль этой величины

и фаза

По этим выражениям на рис. 24.7 построены асимптотическая л. а. х. и л. ф. х. Нетрудно

видеть, что этот случай по расположению фазовой характеристики сводится к случаю л. а. х. типа 2—1—2, изображенной на рис. 12.13. Используя полученные в главе 12 формулы, получаем требуемую протяженность участка с наклоном 20 дб/дек в оптимальном случае;

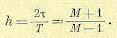(24.21)

Далее, имеем связь между постоянной времени т и базовой частотой:

откуда находим общий коэффициент усиления

(24.22)

Эту формулу можно записать также в следующем виде:

(24.23)

Формулы (24.21) и (24.22) позволяют выбрать значения общего коэффициента усиления непрерывной части К и постоянной времени τ при заданном значении периода повторения Т или определить значение периода повторения при заданном значении общего коэффициента усиления К. Заметим, что в рассматриваемой системе коэффициенты ошибок с0 и c1 равны нулю, а общий коэффициент усиления равен добротности системы по ускорению;

Формула (24.23) дает возможность определить допустимое соотношение между добротностью системы по ускорению К и периодом дискретности Т.

Построение переходного процесса можно произвести аналогично примеру 1 § 24.1.

§ 24.2. О синтезе систем регулирования с ЦВМ

Синтез систем регулирования с ЦВМ наиболее просто производить на основе той методики, которая была изложена в § 12.6 для непрерывных систем. Покажем, как можно перенести ее на дискретные системы регулирования.

Как и в случае непрерывных систем, будем определять качество переходного процесса устойчивых дискретных систем, точнее их запас устойчивости, по показателю колебательности, соответствующему максимуму амплитудной частотной характеристики замкнутой системы:

(24.24)

Соотношение (24.24) полностью аналогично соответствующему соотношению для непрерывных систем. Поэтому получение требуемого показателя колебательности может быть обеспечено выполнением условия для л. а. х. разомкнутой системы подобно тому, как это было сделано в § 12.6 для непрерывных систем.

Для упрощения выкладок ограничимся рассмотрением систем с астатизмом не выше второго порядка, хотя методика остается применимой и в случае более высокого порядка астатизма. Пусть передаточная функция непрерывной части разомкнутой системы имеет вид

При построении л. а. х. следящей системы с учетом ЦВМ введем следующие предположения.

1.Величина, обратная периоду дискретности Т, больше половины частоты среза (wср л. а. х. непрерывной части системы, т. е. wсрT < 2. При расчете следящих систем с ЦВМ это неравенство приходится выполнять практически во всех случаях в связи с требованиями по устойчивости и запасу устойчивости.

2.Все постоянные времени T1 . . ., Тn можно разделить на две группы. К первой группе Т1, . . ., Тq отнесем те из них, которым соответствуют сопрягающие частоты,

меньшие частоты среза wср (большие постоянные времени). Ко второй группе Тq+1, . . ., Тn отнесем те постоянные времени, которым соответствуют сопрягающие частоты большие,

чем частота среза wср (малые постоянные времени), причем для каждой постоянной времени второй группы должно выполняться неравенство Тi < Т/2.

3.Постоянным временем τ 1, . . ., τ m соответствуют сопрягающие частоты меньшие, чем частота среза. Это не относится к тем постоянным времени числителя передаточной функции разомкнутой непрерывной части, которые были введены для компенсации некоторых ее полюсов и поэтому после сокращения соответствующих множителей не вошли в окончательное выражение (24.25).

4.Переход оси нуля децибел асимптотической л. а. х. непрерывной части происходит при отрицательном наклоне 20 дб/дек.

Л. а. х. системы с ЦВМ в области низких частот. Рассмотрим построение л. а. х. для (24.25) в области низких частот, т. е. левее частоты среза. Передаточная функция непрерывной части для этой области может быть представлена в виде

Очевидно, что вследствие условия 4 имеем равенство m =q+1. Разложим (24.26) на простые дроби:

(24-27)

где Ni— коэффициенты разложения, добротность по скорости, а KT0= KΩ представляет собой условную

(24.28)

На основании (24.9) дискретная передаточная функция, соответствующая (24.26), будет

(24-29)

где

Перейдем к дискретной частотной передаточной функции посредством использования w-преобразования (15.163) и подстановки (15.164). В результате получим

(24.30)

где абсолютная псевдочастота

Ранее было сделано допущение, что Ti>T/2; поэтому можно считать

(24.31)

откуда окончательно

(24.32)

Сравнение последнего выражения с (24.27) показывает, что в низкочастотной области частотная передаточная функция системы с ЦВМ может быть получена из передаточной функции непрерывной части подстановкой р = j λ и умножением на дополнительный множитель (1 — }КТ/2). Псевдочастота λ в этой области практически совпадает с частотой входного воздействия w, что вытекает из (24.31). Так как было принято, что 2/T>wср, то влияние дополнительного множителя (1 —j λ Т/2) при построении асимптотической л. а. х. можно не учитывать. Поэтому в .низкочастотной области асимптотическая л. а. х. системы с ЦВМ практически сливается с л. а. х. непрерывной части, причем можно положить λ = w. Это дает большие удобства в формировании низкочастотной части л. а. х. проектируемой системы и позволяет полностью использовать ту методику, которая была изложена выше для непрерывных систем.

Л. а. х. системы с ЦВМ в области высоких частот. В соответствии с принятыми условиями передаточная функция непрерывной части для этой области может быть представлена в виде

(24.33)

где частота среза асимптотической л. а. х.

Разложим (24.33) на простые дроби:

(24.34)

Аналогично предыдущему найдем частотную передаточную функцию переходом к псевдочастоте:

(24.35)

Так как Ti < T/2, то можно положить

Учитывая, что

получаем в результате

(24.36)

Это выражение и может использоваться для построения л.а.х., причем .модуль

(24.36)

(24.37)

Начало л. а. х. в высокочастотной области сливается с низкочастотной области в

точке λ =wср.

При построении фазовой характеристики следует учитывать появление множителя (1-j λ T/2), соответствующего неминимально-фазовому звену. Для построения фазовой характеристики можно воспользоваться результирующим выражением для дискретной частотной передаточной функции, которое на основании изложенного будет

(24.38)

Результирующий фазовый сдвиг

(24.39)

В районе частоты среза при λ < 2/T можно считать с достаточной точностью

(24-40)

В результате при построении высокочастотного «хвоста» приходится учитывать сумму малых постоянных времени Ti и дополнительный множитель (1 — j λ T/2). Последний приводит к подъему л. а. х. на высоких частотах и дает дополнительный фазовый сдвиг в отрицательную сторону, равный λ T/2. Методика расчета следящих систем с ЦВМ и здесь совпадает с методикой расчета непрерывных систем, изложенной выше. Только формула (12.96) должна быть переписана в виде

(24.41)

Аналогичным образом для «несимметричных» л. а. х. типа 1—2—3... (рис. 12.18) систем с астатизмом первого порядка можно показать, что вид л. а. х. в низкочастотной области сохраняется, а требуемый запас устойчивости получится при

граничной частоты происходит при наклоне асимптоты 40 дб/дек так, как это показано на рис. 24.8. Тогда уравнение высокочастотной части будет

(24.44)

где wв = k — частота пересечения оси частот асимптотой, имеющей отрицательный наклон 40 дб/дек.

Раскладывая выражение (24.44) на простые дроби, переходя к Wв (z), а затем к Wв*(j λ ), получим аналогично формуле (24.36) для высокочастотной части

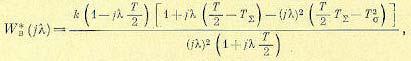(24.45)

где

Если выполняется условие, то формула (24.45) упрощается:

(24.46)

В соответствии с выражением для Wв* (j λ ) строится высокочастотная часть л. а. х., которая показана на рис. 24.8 пунктиром.

Построение фазовой характеристики делается аналогично изложенному выше. Таким же способом строится высокочастотная часть л. а. х. при пересечении

граничной частоты асимптотой 60 дб/дек, 80 дб/дек и т. д. Во всех случаях формирование высокочастотной части делается по сумме малых постоянных времени, которым соответствуют сопрягающие частоты, находящиеся правее граничной частоты w = 2/Т.

Пример. Произведем расчет следящей системы с астатизмом второго порядка при следующих исходных данных:

1) максимальная входная скорость Ωmax = 10 град/сек,

2)максимальное входное ускорение εmax = 5 град/сек;

3)максимальная допустимая ошибка θmax = 2 угл. мин.;

4)непрерывная часть содержит постоянные времени Т1 = 0,01 сек, Т2 = 0,002 сек и Т3 = 0,001 сек;

5)допустимый показатель колебательности М = 1,5 и М = 1,2.

Требуется определить параметры непрерывной части системы и допустимый период повторения ЦВМ.

Решим задачу вначале для случая Т1 = T2 = Т3 = 0 и М = 1,5. Передаточная функция непрерывной части разомкнутой системы, структурно

устойчивой в замкнутом состоянии, должна иметь вид

где τ1 — постоянная времени, вносимая корректирующим звеном

дифференцирующего типа.

Так как высокочастотная часть после частоты среза в рассматриваемом идеализированном случае представляет собой прямую с наклоном 20 дб/дек, то вся частотная передаточная функция системы с ЦВМ может быть получена подстановкой р = jw, где w — псевдочастота, и введением дополнительного множителя (1 — jwТ/2):

Л. а. х. для нее построена на рис. 24.9, а.

На этом же рисунке построена запретная зона для л. а. х. на основании условий по точности и в соответствии с рис. 12.11. Базовая частота (12.76)

Требуемое значение общего коэффициента усиления при совпадении первой асимптоты л. а. х. с границей запретной зоны (рис. 12.24)

Всоответствии с расчетом, проделанным выше, для л.а.х., изображенной на рис.

12.14и рис. 24.7, получаем требуемое значение постоянной времени

Частота среза л. а. х.

В соответствии с формулой (24.41) получаем далее

откуда допустимый период дискретности Т <0,0568 сек. В случае учета постоянных времени Т1, T2 и Т3 имеем

и допустимый период дискретности Т7 <0,0308 сек.

Аналогичные расчеты для случая М = 1,2 дают τ 1 = 0,2 сек, wср = 30 сек-1 и Т < 0,0368 сек (при Т1 = Т2 = Т3 = 0) и Т < 0,026 сек (при Т1 ≠ 0, T2 ≠ 0 и T3 ≠ 0).

На рис. 24.9, б для иллюстрации построены переходные процессы при воздействии на входе в виде единичной ступенчатой функции. Переходные процессы построены посредством разложения в ряд Лорана z-преобразования выходной величины.

Таким образом, синтез следящих систем методом л. а. х. на основе частотных критериев качества (по точности и запасу устойчивости) оказывается применимым и для систем, содержащих в своем контуре ЦВМ. При этом все расчеты сохраняют свою простоту и наглядность.

Для расчета удобно применять абсолютную псевдочастоту, которая в области низких частот (левее частоты среза) совпадает с обычной угловой частотой w. При этом в области высоких частот л. а. х. приходится строить по сумме малых постоянных времени. Влияние квантования по времени, вносимое ЦВМ, легко учитывается при построении только л. а. х., без необходимости рассмотрения фазовой характеристики.

Для облегчения процесса синтеза можно ввести понятие типовых л. а. х. систем регулирования с ЦВМ. На рис. 24.10, а приведены типовые л. а. х. для статической системы и астатической первого и второго порядков без учета временного запаздывания. На рис. 24.10, б изображены соответствующие им л. а. х. непрерывной части, а в табл. 24.1 приведены передаточные функции.

Синтез непрерывных корректирующих средств. При использовании для коррекции системы непрерывных средств возможно применение корректирующих средств трех основных видов: последовательных, параллельных и обратных связей (рис. 10.1).

Наиболее просто производится расчет корректирующих средств последовательного типа. В этом случае дискретная передаточная функция разомкнутой системы должна равняться желаемой передаточной функции

(24.47)

Здесь WпкWо (z) представляет собой дискретную передаточную функцию последовательно включенных корректирующего звена с передаточной функцией W0(р) и непрерывной части с передаточной функцией W0 (p). Напомним, что поэтому расчет