
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf

Здесь интеграл будет всегда положительным, так как функция f(х3) нечетная (см. условие (17.54)). Поэтому V есть знакоопределенная положительная «функция, если γ >1,
обращающаяся в нуль на отрезке установившегося процесса АВ (рис. 17.13).
Поверхности V (х1, х2, х3) = С окружают этот отрезок (рис. 17.13, б), стягиваясь к нему с уменьшением С. Составим производную от функции Ляпунова:
причем частные производные возьмем из (17.67), а производные по безразмерному времени — из уравнений системы (17.63). Тогда
Представим это в виде
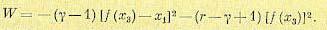 (17.68)
(17.68)
Эта функция W знакопостоянная, так как она не включает в себя координату х2, а потому обращается в нуль не только на отрезке установившегося процесса АВ, а на всей полосе шириной АВ в плоскости х2х3 (рис. 17.13, в).
Но вне этой полосы согласно (17.68) она будет всюду отрицательной при
 (17.69)
(17.69)
Поэтому согласно теореме Ляпунова об устойчивости выражение (17.69) является достаточным условием устойчивости рассматриваемой нелинейной системы самолета с курсовым автопилотом (при любой кривизне и любом наклоне характеристики двигателя, имеющей вид рис. 17.12, б).
Траектория изображающей точки М будет пересекать поверхности V = С
извне внутрь везде, где W = dVdτ
изображающая точка М там, где W обращается в нуль (помимо отрезка установившегося процесса АВ). В данном случае речь идет о том, не останется ли изображающая точка на полосе (показанной на рис. 17.13, е) где W= 0, если она случайно на нее попадет.
Для решения этого вопроса найдем проекции скорости изображающей точки М dxdτ1 , dxdτ2 , dxdτ3 когда эта точка находится в любом месте указанной полосы. Поскольку там
то искомые проекции скорости согласно (17.63) будут
Таким образом, если изображающая точка М попадет на указанную полосу вне отрезка АВ (рис. 17.13, в), то она не останется в ней, а пройдет ее поперек по прямой, параллельной оси x3, с постоянной скоростью, равной γ х2, как показано стрелками на

рис. 17.13, в. Пройдя полосу, изображающая точка снова будет пересекать поверхности V= С извне внутрь, т. е. данная система регулирования будет устойчивой.
Случай 0 <γ < 1. Для этого случая возьмем функцию Ляпунова в виде
Производная от нее будет
Отсюда аналогично предыдущему приходим к достаточному условию устойчивости системы в виде
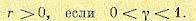 (17.70)
(17.70)
Общий вывод. Полученные в данной задаче достаточные условия устойчивости (17.69) и (17.70) после Подстановки выражений γ и r через параметры системы (17.64) принимают
вид соответственно
Первое из этих условий устойчивости говорит о том, что передаточное число обратной связи надо сделать достаточно большим, если производная pψ введена в закон
регулирования недостаточно интенсивно. Из второго же условия устойчивости следует, что система будет устойчива при любой обратной связи, если передаточное число по производной достаточно велико.
Как видим, данные условия устойчивости не зависят от формы характеристики двигателя (рис. 17.12, б), т. е. они одинаковы при любой кривизне, любом наклоне и любой зоне застоя (в том числе и при однозначной релейной характеристике двигателя постоянной скорости, а также и при линейной характеристике). Такие условия называются условиями абсолютной устойчивости. Они гарантируют, что при их выполнении система будет наверняка устойчива при любой нелинейности с ограничением лишь (17.54). В действительности же система может быть устойчивой и в некоторой области за пределами этих условий устойчивости при конкретно заданной форме нелинейности (см. гл. 18).
Пример учета нелинейности измерителя регулируемой величины. На основании вышеизложенных теорем Ляпунова М. А. Айзерман показал, что если уравнение системы содержит нелинейность
 (17,71)
(17,71)
где F(хk) — однозначная нелинейная функция, обращающаяся в нуль при хk = 0, а k — любое целое число из 1, 2, . . ., n, то для устойчивости системы достаточно, чтобы для

линеаризованной системы (17.71) при замене F(хk) =a хk можно было построить функцию Ляпунова V, производная от которой W является знакоопределенной отрицательной функцией при любом значении а в интервале a1<a<а2, если кривая F(хk) лежит между прямыми F= а1 хk и F= а2 хk, как изображено, например, на рис. 17.14,а. Пусть, например, в прежней системе самолета с курсовым автопилотом (рис. 17.12, а) уравнение регулируемого объекта имеет вид (17.55), привод руля имеет линейную характеристику pδ = k8U , но реостат при чувствительном элементе I(измерителе регулируемой величины
ψ ) имеет нелинейную характеристику, в результате чего получается нелинейное уравнение автопилота
где
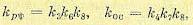 (17.72)
(17.72)
а F(ψ ) — нелинейная функция, например, вида рис. 17.14, б. Введем обозначения переменных;
Тогда уравнения автопилота (17.72) и самолета (17.55) примут вид (17.71), а именно:
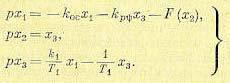 (17.73)
(17.73)
Зададимся функцией V в виде
где все шесть коэффициентов b неизвестны. Потребуем, чтобы функция
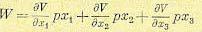 (17.74)
(17.74)
при фиксированном значении F(х2) = а0х2 в уравнениях (17.73) имела вид
Тогда путем приравнивания соответствующих коэффициентов выражений (17.74) и (17.75) можно найти все шесть величин b из системы шести алгебраических уравнений. Здесь приводится результат решения только для трех коэффициентов, которые понадобятся в дальнейшем, а именно:
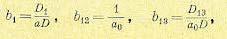 (17.76)
(17.76)
где
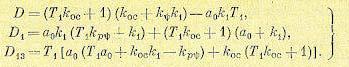 (17.77)
(17.77)
Затем потребуем, чтобы выражение (17.74) при замене в уравнениях (17.73) F(х2) = ах2, гдё а = а0 + ∆а, имело вид
что дает значения:
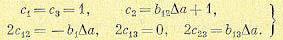 (17.78)
(17.78)
Функция W будет знакоопределенной отрицательной, как требуется по условию, если

Эти неравенства с учетом (17.78) приводятся к следующему:
Подставив сюда (17.76), увидим, что это условие выполняется, если ∆а лежит в интервале ∆а1 <; ∆а < ∆а2, где
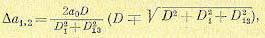 (17.79)
(17.79)
откуда видно, что ∆a1 <0 и ∆а2 > 0. При этом требуется еще D>0. Нетрудно проверить, что последнее требование совпадает с критерием устойчивости (см. § 6.2) для данной системы в линеаризованном виде при замене F(ψ ) = a0ψ (рис. 17.14, б), так как
характеристическое уравнение согласно (17.55) и (17.72) в этом случае будет
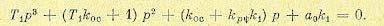 (17.80)
(17.80)
Итак, для устойчивости рассматриваемой нелинейной системы автоматического регулирования достаточно, во-первых, чтобы выполнялся критерий устойчивости Гурвица D>0 для линеаризованной системы при F(ψ ) = a0ψ и, во-вторых, чтобы нелинейная
характеристика F(ψ) измерителя регулируемой величины лежала, как указано на рис.
17.14, б, между прямыми F = a1ψ и F = a2ψ ; причем a1 = a0 + ∆a1, а2 = a0 + ∆а2 где значения ∆a1,2 определяются формулой (17.79), в которой величины D, D1)из согласно (17.77) выражаются через параметры данной системы и через первоначально принятое значение a0 при линеаризации F(ψ ) = a0ψ .
Как и в предыдущем примере, здесь получаются условия абсолютной устойчивости, т. е. условия, не зависящие от формы нелинейности, но в более узких, чем (17.54), пределах, показанных на рис. 17.14, б.
§ 17.3. Определение автоколебаний релейных систем методом припасовывания
В § 17.1 с помощью фазовой плоскости были найдены автоколебания некоторых нелинейных систем второго порядка. Еще ранее, в § 16.1, были исследованы автоколебания в релейной системе второго порядка методом припасовывания. Однако и для релейных систем любого порядка также существует точное аналитическое решение, потому что релейные характеристики проще других нелинейных тем, что выходная величина принимает только определенные постоянные значения ±с (а при наличии зоны нечувствительности — еще и нулевое значение). Имеются методы аналитического решения Г. С. Поспелова [95, 121], Я. 3. Цыпкина [135] и др.
Изложим здесь решение А. И. Лурье для релейной системы любого-порядка по методу припасовывания, полагая, что уравнения системы автоматического регулирования имеют вид
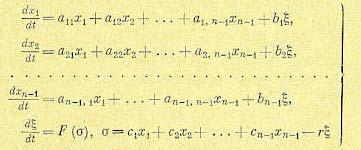 (17.81)
(17.81)
(переменная ξ играет роль переменной хn). Это имеет место, например, для системы с нелинейной характеристикой двигателя в приводе регулирующего органа, причем dξ / dt


Продифференцировав по времени все уравнения (17.86), кроме последнего, и исключив затем из них ру и рξ , получаем канонические уравнения. для заданной системы (17.81) в
виде
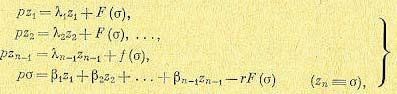 (17.89)
(17.89)
причем z1, z2, . . ., zn-1 и а называются каноническими переменными (а играет роль переменной z). Эти уравнения имеют значительно более простой вид, чем исходные уравнения (17.81), что и позволяет провести дальнейшие исследования в более простом и общем виде.
Следует заметить, что вещественным корням λ соответствуют вещественные канонические переменные z, а комплексным корням — комплексные канонические переменные.
Теперь требуется написать только выражения для исходных переменных (х1, х2, ..., Хn- 1,ξ ) через канонические (z1, z2, ..., zn-1,σ ). Получим их.
Если все корни λj отличны от нуля, то из (17.88) имеем
Подставляя это с учетом (17.85) в уравнения (17.84), находим выражения исходных переменных через канонические в виде
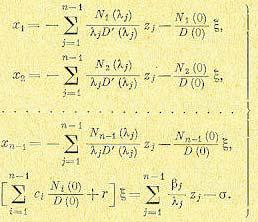 (17.90)
(17.90)
Если же один из корней многочлена D(р) равен нулю, например
В результате вместо (17.90) получаем формулы:

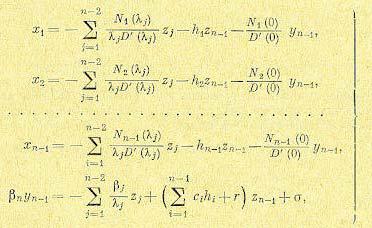 (17.91)
(17.91)
где
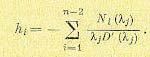 (17.92)
(17.92)
По последней из формул (17.91) определяется уn-1 и подставляется во все предыдущие. Рассмотрим случай, когда релейная характеристика Р (а) имеет гистерезисную петлю без зоны нечувствительности (рис. 17.15). В частном случае b = 0 это будет идеальная релейная характеристика. Искомые автоколебания предполагаются симметричными, т. е. вторая половина периода колебаний повторяет первую с обратным знаком (несимметричные автоколебания могут встретиться только в редких случаях). Обозначим половину периода автоколебаний через Т. В течение одной половины периода, когда σ >0 и согласно рис. 17.15 F(σ ) = с, уравнения (17.89) имеют вид
Если корни λj не равны нулю, то общее решение этих уравнений будет
где С1,С2, . . ., Сn — произвольные постоянные интегрирования. Они определяются из условий периодичности, выражающих собой тот факт, что в конце полупериода
колебаний каждая переменная должна быть равна ее значению в начале периода с обратным знаком а именно:
если время t отсчитывать от начала рассматриваемого полупериода колебаний. В результате получаем:

Следовательно, написанное выше решение имеет вид
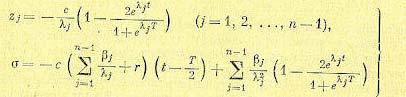 (17.93)
(17.93)
в интервале времени 0 < t< Т.
В начале полупериода (в момент переключения реле) согласно рис. 17.15 имеем σ = b . Подставив это в (17.93), получаем уравнение для определения полупериода автоколебаний Т:
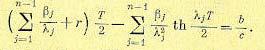 (17.94)
(17.94)
Период автоколебаний будет 2Т. Следовательно, частота автоколебаний
Необходимо заметить, что для того, чтобы действительно произошло переключение реле, нужно согласно рис. 17.15 иметь возрастание величины σ при σ = b, т. е. в этот момент должно быть рσ > 0. Отсюда получается, что должно выполняться следующее условие переключения:
 (17.95)
(17.95)
Кроме того, не должно быть обратного переключения реле внутри полупериода, т. е. требуется σ > -b при 0 < t <Т. Это можно проверить, построив кривую σ (t) по второй из формул (17.93).
Амплитуда автоколебаний для любой переменной определяется как максимальное ее значение внутри полупериода (0 < t < Т) на основании формул (17.93). Последние дают также и всю кривую автоколебательного процесса на участке 0 < t< T (на втором полупериоде она повторяется с обратным знаком, затем с прежним знаком и т. д.).
В случае, если один из корней λj , равен нулю, например λn−1 = 0, то формулы (17.93), (17.94) и (17.95) заменяются соответственно следующими:
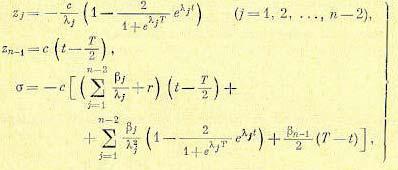 (17.96)
(17.96)
а также
(17.97)


 (17.57)
(17.57)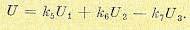 (17.58)
(17.58)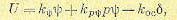 (17.59)
(17.59)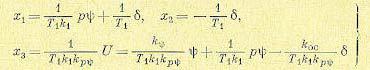 (17.61)
(17.61)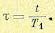 (17.62)
(17.62)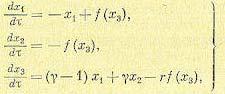 (17.63)
(17.63)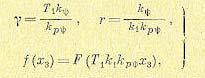 (17.64)
(17.64)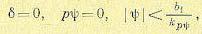 (17.65)
(17.65)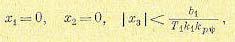 (17.66)
(17.66)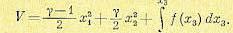 (17.67)
(17.67)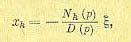 (17.82)
(17.82)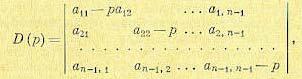 (17.83),
(17.83),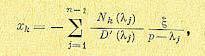 (17.84)
(17.84) (17.85).
(17.85).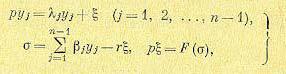 (17.86)
(17.86)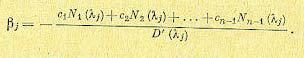 (17.87),
(17.87),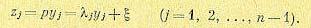 (17.88)
(17.88)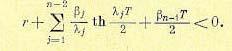 (17.98)
(17.98)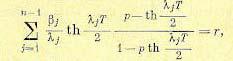 (17.99)
(17.99)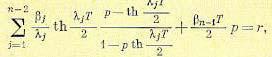 (17.100)
(17.100)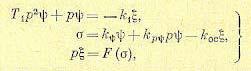 (17.101)
(17.101) (17.102)
(17.102)