
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf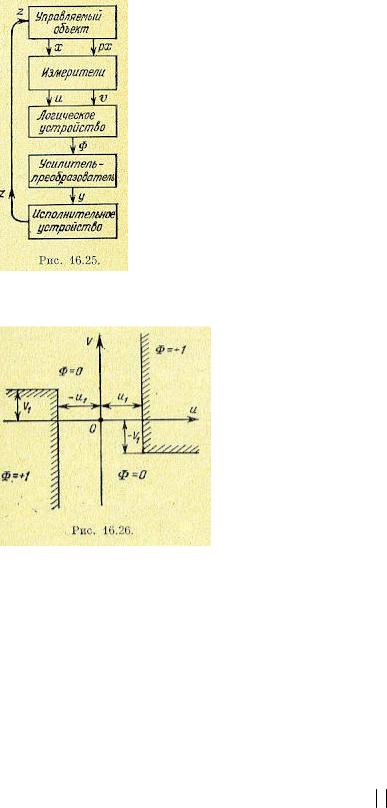
 (16.68)
(16.68)
Уравнение исполнительного устройства
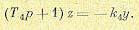 (16.69)
(16.69)
Кроме того, должна быть задана логика формирования нелинейного закона регулирования Ф(u, v), которая может быть назначена или синтезирована в очень разнообразных формах для обеспечения простоты и надежности аппаратуры,
наибольшего быстродействия, наименьшей затраты энергии на управление, учета ограничения мощности источника энергии и специфики желательных режимов его работы и т. п.
Выбранную тем или иным образом логику формирования нелинейного закона управления можно записывать в аналитической форме. Однако во многих случаях удобнее изображать ее графически на плоскости входных величин логического устройства (u, v).
Для примера рассмотрим простейшую логику (рис. 16.26):
Смысл ее заключается в следующем. Величины u и v, согласно уравнениям (16.67), с точностью до постоянных времени соответствуют отклонению регулируемой величины x и ее первой производной по времени рх. Поэтому наличие порогового значения u1 соответствует тому, что при малых х исполнительное устройство не работает (Ф=0). Не работает оно также и при больших отклонениях x, но только тогда, когда имеется достаточная по величине скорость рх (соответствующая превышению порога ±v1) со знаком, противоположным знаку x, ибо в этом случае отклонение х уменьшается по величине само собой даже при неработающем исполнительном устройстве системы управления. Исполнительное устройство включается (Ф = +1 или Ф =-1, рис. 16.26) только
тогда, когда при .достаточно больших отклонениях х ( u >u1) скорость рх имеет тот те знак
(т. е. отклонение возрастает по величине) либо когда скорости рх имеет противоположный знак, но мала (| v | <v1).
Система с переменной структурой. Как уже указывалось в начале книги (§ 2.3), системы с переменной структурой содержат в себе специальное переключающее устройство для изменения структуры регулятора, которое срабатывает в зависимости от размеров и знаков входных величин.
Примеры переключающих устройств приведены схематически на рис. 16.27, где КЭ — ключевой элемент, БИС — блок изменения структуры. Уравнение принято [42] записывать в виде
 (16.70)
(16.70)
Функция Ψ может строиться по-разному. Например (рис. 16.27, а),
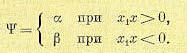 (16.71)
(16.71)
Для случая, указанного на рис. 2.9 и 2.10
 (16.72)
(16.72)
Под символами α и β могут также иметься в виду различные выражения: в простейшем случае постоянные
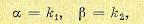 (16.73)
(16.73)
в другом случае
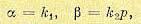 (16.74)
(16.74)
и любые другие, в том числе и нелинейные.
Основная же характерная нелинейность здесь состоит в самом факте автоматического переключения в зависимости от состояния входных величин.
Г Л А В А 17
ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ
§ 17.1. Фазовые траектории и метод точечных преобразований
Понятие о фазовом пространстве, о фазовых траекториях и их типах было уже дано выше. В данном параграфе на примерах построения фазовых траекторий для простейших систем второго порядка будут проиллюстрированы некоторые важные особенности процессов в нелинейных системах автоматического регулирования.
Пример 1. Возьмем систему автоматического регулирования с объектом без самовыравнивания и с приводом регулирующего органа, имеющим постоянную скорость. Уравнение регулируемого объекта без самовыравнивания будет
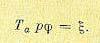 (17.1)
(17.1)
Для регулятора без массы ;и демпфера с жесткой обратной связью, т. е. при
δη = −ϕ,σ =η −ξ,ξ =ζ , получим
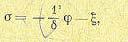 (17.2)
(17.2)
где η,ϕ,σ,ξ,ζ — относительные изменения регулируемой величины, смещений
чувствительного элемента, регулирующего органа, элемента обратной связи и управляющего золотника (рис. 10.11, а), δ — коэффициент. Привод регулирующего органа пусть имеет постоянную скорость в двух вариантах: 1) с мгновенным переключением (рис. 16.22, ж) при переходе управляющего элемента (золотника, струйной трубки) через нейтральное положение (σ = 0); 2) с зоной нечувствительности (рис. 16.22, з) вследствие наличия «перекрытия» золотника или струйной трубки. В первом случае уравнение привода регулирующего органа будет
 (17.3)
(17.3)
а во втором
 (17.4)
(17.4)
Возьмем фазовую плоскость (х, у), приняв
 (17.5)
(17.5)
Из уравнений (17.1), (17.2) и (17.5) имеем
 (17.6)
(17.6)
Следовательно, переключения привода в первом варианте (σ = 0) будут иметь место при
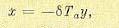 (17.7)
(17.7)
что соответствует прямой АВ (рис. 17.1, а) на фазовой плоскости, причем согласно (17.16) значениям σ >0 соответствует часть плоскости слева от прямой АВ, а σ < 0 — справа. На основании первого из соотношений (17.6) с учетом (17.3) при σ < 0 получаем
 (17-8) а из (17.5)
(17-8) а из (17.5)
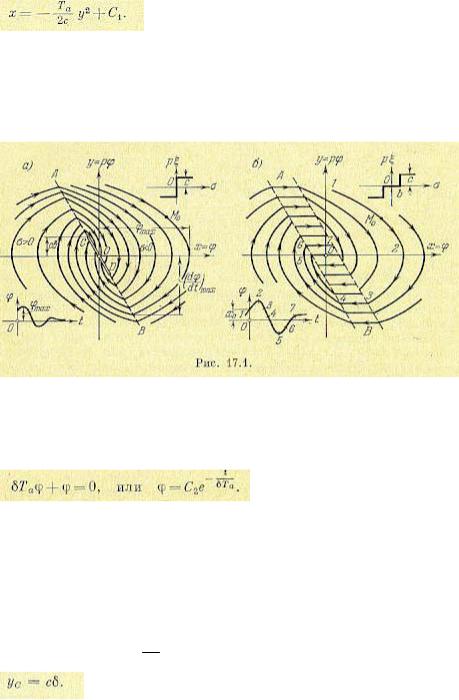
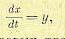 (17.9)
(17.9)
откуда находим уравнения фазовых траекторий
 (17.10)
(17.10)
или, после интегрирования,
Это есть семейство парабол, показанное на рис. 17.1, а справа от линии АВ (они симметричны относительно оси х). Так как (17.8) и (17.9) являются проекциями скорости V изображающей точки М на оси х и у, то имеем vу < О,
а знак vx совпадает со знаком у. В соответствии с этим на рис. 17.1, а укажем стрелочками направление движения изображающей точки М по фазовым траекториям. Аналогичным путем легко строятся параболы слева от прямой АВ.
В результате, как видно из общего расположения фазовых траекторий (рис. 17.1, а), получается устойчивая система с затухающим колебательным переходным процессом. Но число колебаний будет конечным. В самом деле, здесь имеется особый отрезок СD, в который вливаются все фазовые траектории. Чтобы выявить поведение системы на этом отрезке, вспомним, что для него согласно (17.7) и (17.5)
Следовательно, попав на отрезок СD, изображающая точка не может с него уйти, и система будет апериодически приближаться к установившемуся состоянию, т. е. изображающая точка будет сползать по отрезку СD к началу координат 0. Таким образом, имевший место вначале колебательный переходный процесс после конечного числа колебаний вырождается в этот так называемый скользящий процесс.
Крайние точки особого отрезка СD определяются, очевидно, как точки, в которых прямая АВ касается одной из парабол соответственно правого и левого семейств. Поэтому,
подставив значения dydx из (17.7) в выражение (17.10), найдем точку С:
По найденной картине расположения фазовых траекторий можно качественно представить себе кривую переходного процесса ϕ (t) при любых начальных условиях.
Начальными условиями определяется начальное положение изображающей точки М и тем самым — определенная фазовая траектория, иллюстрирующая протекание процесса. Она показывает (рис. 17.1, а) максимальное отклонение регулируемой величины фтаХ1 максимальную скорость (рϕ )mах; а также все последующие отклонения, число колебаний
и т. п.

Рассмотрим теперь ту же систему, но с учетом зоны нечувствительности. В этом случае переключениям привода (при σ = -b и σ = +b) на фазовой плоскости соответствуют согласно (17.6) две наклонные прямые (рис. 17.1, б):
Между этими прямыми |σ | < b, правее их σ <b, левее их σ >b (причем b >0).
При | σ | < b из (17.4), (17.6) и (17.5) получаем
откуда (при у≠ 0 )
(прямые, параллельные оси х в полосе АВ на рис. 17.1, б).
При | σ | > b получим прежние параболы. В результате снова система оказывается устойчивой и имеет колебательный переходный процесс, но вместо
особой точки О получаем особый отрезок (у = 0, - bδ < х < bδ ), т. е. установившееся состояние определяется неоднозначно. Это соответствует тому, 'что регулятор может находиться в равновесии в любом месте внутри зоны нечувствительности. Здесь точно так же возможен скользящий процесс, как x в случае рис. 17.1, а.
В данном примере система оказывается устойчивой при любых значениях параметров и при любых начальных условиях. Однако здесь для получения системы второго порядка была проведена грубая идеализация уравнений регулятора (пренебрежение массой и демпфированием).
Пример 2. Допустим, что требуется стабилизировать угловое положение некоторого тела, когда сопротивлением среды его вращению можно пренебречь. Уравнение объекта будет
 (17.11)
(17.11)
где J— момент инерции тела, ϕ — угол поворота тела, w — его угловая скорость, М —
управляющий момент со стороны исполнительного органа системы стабилизации. Уравнение регулятора (системы стабилизации) запишем в виде
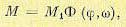 (17.12)
(17.12)
где М1 — постоянная положительная величина, Ф (ϕ ,w) — нелинейный закон
регулирования, осуществляемый при помощи логического устройств по тому же простейшему принципу, что и на рис. 16.26, с той лишь разницей, что по углу ϕ фазовая
плоскость ограничена значениями +π и -π , так как это составляет один полный оборот тела (рис. 17.2).

Изобразим процесс регулирования на фазовой плоскости. Уравнение» всей системы согласно (17.11) и (17.12) будет
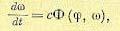 (17.13),
(17.13),
где обозначено
причем с имеет физический смысл величины углового ускорения, сообщаемого данному телу постоянным моментом М1.
Умножив почленно уравнение (17.13) на выражение
получим дифференциальное уравнение фазовой траектории
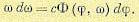 (17.14)
(17.14)
Это уравнение легко интегрируется внутри участков, на которых Ф = const. В результате для каждого отдельно взятого участка уравнение фазовой траектории будет
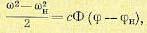 (17.15)
(17.15)
где ϕн и wн — значения ф и со в начальной точке данного участка.
Зададим начальные условия процесса:
Для данной начальной точки процесса (см. рис. 17.2) имеем Ф = 0. Поэтому на первом участке процесса согласно (17.15) уравнение фазовой траектории будет
Этот участок движения с постоянной скоростью заканчивается в точке 1 (рис. 17.2), где происходит включение исполнительного органа (Ф = -1). Следовательно, для второго участка процесса (после точки 1) из (17.15) получим уравнение фазовой траектории
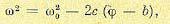 (17.16)
(17.16)
так как в начальной точке 1 этого участка ϕн = b, wн = w0. Фазовая траектория (17.16) — парабола, ось которой совпадает с координатной осью ϕ . Это соответствует
равнозамедленному движению ( |
dw |
= −c ) Изображая параболу графически, доводим ее |
|
dt |
|||
|
|
до границы ϕ = π (участок 1—2 на рис. 17.2), причем в точке 2 согласно (17.16)
 (17.17)
(17.17)
Это значение переносим в точку 2' (для вращающегося тела ϕ = ±π это одна и та же
точка). Здесь происходит выключение исполнительного органа (Ф = 0). Поэтому дальнейшее движение согласно (17.15) пойдет с постоянной скоростью
до точки 3 (рис. 17.2). Таким образом, в рассмотренной начальной части процесса регулирования тело совершило один полный оборот, но в конце этого оборота скорость вращения его стала меньше начальной.
В точке 3 снова включается исполнительный ^орган (Ф = - 1), в результате чего фазовая траектория будет
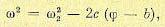 (17.18)
(17.18)
так как в точке 3 ϕ = b , wн = w2. Допустим, что соответствующая уравнению (17.18) парабола 3 — 4 не доходит до границы ϕ =π . Это означает, что тело больше не совершит
полного оборота, а начнет (с точки А) возвращаться в сторону нулевого положения. В точке 4 (рис. 17.2) имеем скорость w4 =- b1. Следовательно, из (17.18) угловая координата ее будет

где w2 определяется по формуле (17.17). Дальше (4 — 5) процесс пойдет-с постоянной скоростью (так как Ф = 0), после чего тело войдет в установившийся автоколебательный режим, определяемый предельным циклом (5—6—7—8). Уравнение параболы 7—8 согласно (17.15) будет
Отсюда амплитуда угловых автоколебаний аф, как значение ф при w = 0, будет
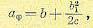 (17.19),
(17.19),
а амплитуда колебаний скорости
Она равна зоне нечувствительности измерителя угловой скорости b1, в то время как амплитуда угловых колебаний (17.19) несколько больше зоны нечувствительности измерителя угла b.
Период автоколебаний tа можно вычислить как сумму времен:
где tхол и tраб — времена участков (6—7) + (8—5) и (5—6) + (7—8) соответственно. По законам равномерного и равнозамедленного движений соответственно получаем
Итак, установившийся режим стабилизации в данной системе является автоколебательным. Однако уравнение системы (17.13) справедливо только для идеальной системы стабилизации. Всякое реально имеющееся запаздывание в работе усилительнопреобразовательного и исполнительного устройств приведет к увеличению амплитуд автоколебаний по сравнению с полученными здесь значениями. Решение задачи с учетом постоянных времени системы управления будет дано в следующей главе.
Пример 3. Уравнения системы автоматического регулирования курса водяной торпеды в упрощенном варианте имеют вид: линейная часть (16.40) и (16.41), т. е.
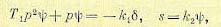 (17.20)
(17.20)
и нелинейное звено (возьмем сначала один случай)
 (17.21)
(17.21)
Покажем, что здесь равновесное установившееся состояние системы с постоянным значением ψ = 0 неустойчиво, но будет иметь место устойчивый автоколебательный
процесс.
Возьмем фазовую плоскость (х, у) с координатами х = -ψ , у = рψ (угол отклонения и
угловая скорость отклонения оси торпеды от заданного курса). Уравнения (17.20) и (17.21) перепишутся в виде
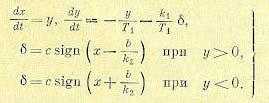 (17.22)
(17.22)
Из сравнения этих уравнений с упрощенными уравнениями системы регулирования температуры в конце § 16.1 видна их полная аналогия. Поэтому здесь, так же как и в случае рис. 16.15, установившийся процесс движения торпеды будет автоколебательным, причем картина фазовых траекторий будет иметь вид, показанный на рис. 17.3, а.
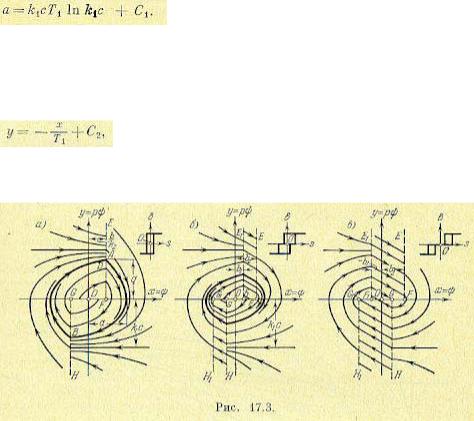
В качестве ординаты фазовой плоскости здесь удобнее взять не скорость отклонения регулируемой величины dUdt , как делалось раньше, а вторую переменную ∆I 2 . Итак,
примем для этой задачи
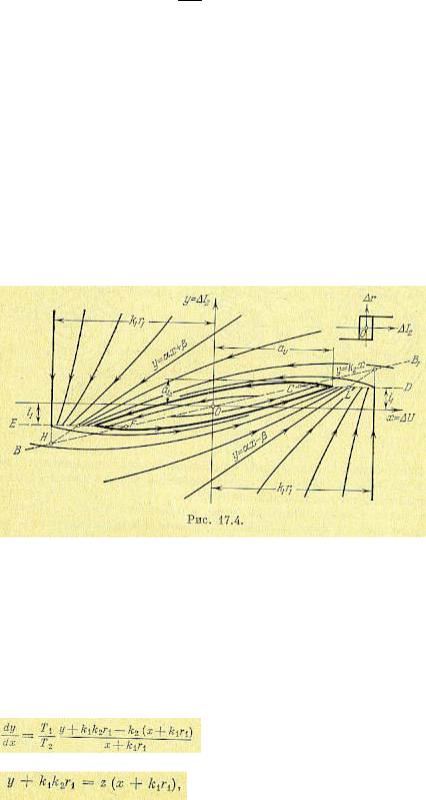
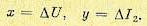 (17.26)
(17.26)
Тогда уравнения (17.24) преобразуются к виду
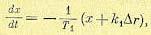 (17.27)
(17.27)
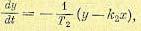 (17.28)
(17.28)
где согласно (17.25), (17.26) и (17.28) имеем
 (17.29)
(17.29)
следовательно, первое из этих условий имеет место ниже прямой (рис. 17.4), а второе
— выше нее. В первом случае переключение реле происходит при у = i1; т. е. на прямой СD (рис. 17.4), а во втором случае — при у=-i1, т. е. на прямой ЕF. Чертеж сделан в
предположении, что k1k2r1 >i1.В результате получаем, что выше линии ЕFСD будет
 (17.30)
(17.30)
а ниже линии ЕFСD
 (17.31)
(17.31)
Рассмотрим сначала верхнюю область. Для нее, деля (17.28) на (17.27), с учетом (17.30) получим уравнение фазовых траекторий
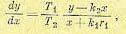 (17.32)
(17.32)
которое можно представить в виде
и проинтегрировать, применив вспомогательную подстановку
где z — новая переменная вместо у. В результате найдем следующее уравнение фазовых траекторий (при Т1 >Т2):
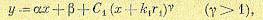 (17.33)
(17.33)
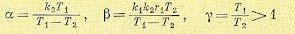 (17.34)
(17.34)
где С1 — произвольная постоянная,

при γ = 1 решение будет иметь другой вид, а при γ <1 будет а < 0 и B< 0; эти решения не
будут исследоваться).
Чтобы представить себе всю совокупность фазовых траекторий, можно провести на фазовой плоскости прямую
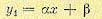 (17.35)
(17.35)
и ко всем ординатам этой прямой добавлять
придавая С1 произвольные значения (каждому значению С1 будет соответствовать определенная фазовая траектория). Это будут параболы степени γ с осью
 (17.37)
(17.37)
и с единым началом в точке Н (рис. 17.4), имеющей координаты
На рис. 17.4 показаны все ветви этих парабол, лежащие выше линии ЕFСD (так как только там справедливы данные выкладки). Направления стрелок на полученных фазовых
траекториях определяются тем, что проекция скорости изображающей точки υx = dxdt
справа от прямой (17.37) согласно (17.27) будет отрицательна, а слева — положительна;
проекция же υy = dydt согласно (17.28) выше прямой у = k2х будет отрицательна, а ниже —
положительна (во всех точках прямой у= k2x касательные к фазовым траекториям горизонтальны).
Аналогично строятся и все фазовые траектории ниже линии ЕFСD, так как их дифференциальное уравнение отличается от (17.32) только заменой +r1 на —r1 согласно
(17.31).
В результате на рис. 17.4 видим, что все фазовые траектории, исходящие из особого отрезка FОС, расходятся, а все траектории, идущие от краев чертежа, сходятся. Как те, так и другие асимптотически приближаются к установившемуся предельному циклу, обозначенному на чертеже жирной замкнутой кривой (чичевицеобразной). Это соответствует тому, что установившийся процесс в системе является автоколебательным, причем размеры предельного цикла аU и аI2 представляют собой амплитуды автоколебаний соответственно регулируемого напряжения ∆U и тока в обмотке электромагнита реле
∆I 2 .
Определить фазовую траекторию, образующую этот предельный цикл, можно как такую кривую (17.33), у которой
 (17.38)
(17.38)
чем определяется значение произвольной постоянной С1. Значение x (17.38) для этой кривой и дает искомую амплитуду аU. Амплитуда же аI2 определяется как ордината пересечения кривой предельного цикла с прямой у =k2х (ибо, как было показано ранее, в точках этой прямой касательные к фазовым траекториям горизонтальны).
Из чертежа (рис. 17.4) видно, что предельный цикл лежит левее точки L и охватывает точку С. Поэтому хс < аU < хL, т. е. амплитуда автоколебаний регулируемого напряжения заключена в интервале
где а и β определяются формулами (17.34). Амплитуда же aI2 будет немного больше i1.
Пример 5. Рассмотрим следящую систему с сухим трением в управляемом объекте, для которой уравнения были написаны в § 16.3. Уравнение регулируемого объекта (16.52) как нелинейного звена при отсутствий линейного трения (с2 = 0) имеет вид

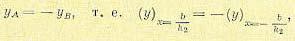 (17.23)
(17.23)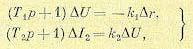 (17.24)
(17.24)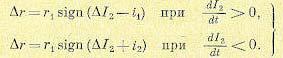 (17.25)
(17.25)