Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

где

причем во второй из формул (13.55) значения ∆x берутся со сдвигом на ∆t вправо по

сравнению с ∆x1 .

Отсюда вытекает следующее построение. Наносим заданные кривые T1(t) и T2(t), а также кривую Т3(t), ординаты которой определяются по второй из формул (13.54). Они показаны на графике (рис. 13.6, а).

На другом графике наносим заданное f(t) (рис. 13.6, 6). На основании заданных начальных условий (см. выше) наносим на последнем графике точки х0, x10 и в середине первого интервала (как в § 7.6) еще точку А с ординатой (7.76), т. е.

Из точки Е1 в середине первого интервала ∆t на кривой f(t) откладываем вниз отрезок

(вниз, когда он положителен, и вверх, когда он отрицателен). При этом величина x( ∆2t )

берется как ордината уже имеющейся точки А, величина T3 ( ∆2t ) берется из графика Т3(t),

а величина х0 — из заданных начальных условий. Из полученной точки Е2 откладываем горизонтальный отрезок

размер которого берется из графика T1 (t). Точку М соединяем прямой линией с точкой x10, что дает новую точку Н1 кривой х1(t) при t = ∆t .

Из точки Н1 откладываем вниз отрезок

равный ординате точки А. Из точки Н2 проводим горизонтальный отрезок

размер которого берется из графика Т2(t). Точку К соединяем с точкой A, что дает новую точку В искомой кривой х (t) в середине второго интервала ∆t . Опишем еще второй шаг интегрирования. Из точки F1 кривой F(t) в середине второго интервала ∆t откладывается вниз отрезок

где хв — ордината точки B, полученной выше; tgα — тангенс угла наклона прямой КА, проведенной ранее (он дает требуемое значение х). Откладываем отрезок

и проводим прямую N1H1, получая при этом новую точку I1 кривой х1(t). Из точки I1 откладываем вниз

а затем вправо

после чего проводим прямую LВ. Это дает новую точку С искомой кривой х(t) и т. д. Все описанные построения можно заменить числовыми расчетами.

§ 13.3. Передаточные функции

Связь между входной и выходной величинами в системе с переменными параметрами определяется интегральной зависимостью (13.9):

Предположим, что к входному сигналу f(t) можно применить преобразование Фурье (7.15). Тогда его можно представить в виде (7.16):

Объединяя записанные выше две формулы, получаем

(13.56)

Здесь в первом интеграле нижний предел взят равным − ∞ . Это отражает тот факт, что входное воздействие может начаться в любой момент времени при t < 0, в том числе и при

t → −∞. Меняя в (13.56) порядок интегрирования и умножая правую часть на e jwt e− jwt , получаем

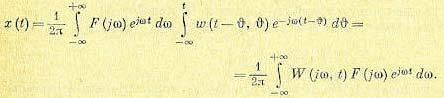(13.57)

Здесь введена частотная передаточная функция системы с переменными параметрами

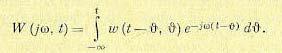(13.58)

Ее можно представить также в следующем виде:

(13.59)

где θ = t −υ — реверс-смещение, а w(θ,t −θ) — сопряженная функция веса (13.7).

Величина, находящаяся в правой части (13.57) под знаком интеграла, представляет собой изображение Фурье функции времени х(t). Поэтому вместо (13.57) можно записать

(13.60)

Таким образом, изображение Фурье выходной величины системы с переменными параметрами можно представить как изображение Фурье входной величины, умноженное на частотную передаточную функцию. Разница по сравнению с системой, имеющей постоянные параметры, заключается в том, что выражение (13.60) записано для некоторого фиксированного момента времени t = const. В связи с этим в частотную передаточную функцию W ( jw,t) входит параметр t, вследствие чего она называется

параметрической частотной передаточной функцией.

Переходя в формуле (13.57) к преобразованию Лапласа, получим

(13.61)

где параметрическая передаточная функция

Будем искать решение в виде ряда

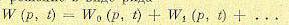(13.72)

Первое приближение можно получить, положив N = 0 в (13.70):

(13.73)

Это будет передаточная функция системы с «замороженными» коэффициентами. Для вычисления первой поправки W1 ( p, t) подставим полученное из (13.73) первое приближение в правую часть (13.70). Тогда получим для первой поправки

(13.74)

(13.75)

Таким образом, последующий член ряда (13.72) получается посредством дифференцирования предыдущего члена в соответствии с (13.71) и подстановки его в

(13.75).

Ряд (13.72) сходится тем быстрее, чем медленнее изменяются коэффициенты исходного дифференциального уравнения (13.1).

По найденной функции W ( p, t) может быть получена параметрическая частотная передаточная функция W1 ( jw, t) подстановкой р = jw.

Использование параметрических передаточных функций. В соответствии с формулой (13.61) изображение Лапласа выходной величины системы с переменными параметрами можно найти как произведение изображения воздействия на параметрическую передаточную функцию:

(13.76)

Это дает возможность находить переходные процессы в системе с переменными параметрами посредством использования преобразования Лапласа (или Карсона — Хевисайда). Для этой цели по формуле (13.76) отыскивается изображение выходной величины, а затем делается переход к оригиналу х (t).

Для этой цели могут использоваться существующие таблицы изображений Лапласа функций времени. Так, например, пусть изображение выходной величины равно

Полагая в этом выражении время t фиксированным параметром, по таблице (см., например, табл. 7.2) находим

Если изображение представляет собой сложную дробно-рациональную функцию, то можно использовать теорему разложения (см. § 7.4). При отсутствии нулевых корней знаменателя изображения

(13.77)

аналогично формуле (7.37) получаем

(13.78)

При наличии одного нулевого корня знаменателя изображения

(13.79)

аналогично формуле (7.39) получаем

(13.80)

В формулах (13.78) и (13.80) корни знаменателя предполагаются некратными. Для построения переходного процесса может также использоваться вещественная частотная характеристика (см. § 7.5). Для общего случая воздействия произвольной

формы из (13.57), аналогично проделанному в § 7.5, можно получить расчетную формулу, являющуюся обобщением формулы (7.52):

(13.81)

где Pϕ (w,t) — вещественная часть частотного изображения искомой функции х (t),

полученного подстановкой в преобразование Карсона — Хевисайда p=j.

В частном случае, когда входное воздействие представляет собой единичную ступенчатую функцию, из (13.57), аналогично проделанному в § 7.5, получается расчетная формула, являющаяся обобщением формулы (7.53) для переходной функции рассматриваемой динамической системы:

(13.82)

где Р (w, t) — вещественная часть параметрической частотной передаточной функции

(13.58).

Построение переходного процесса проводится, аналогично изложенному

в § 7.5, по h-функциям. Разница будет заключаться в том, что построение переходного процесса будет справедливым только для того момента времени t= const, который вошел в качестве параметра в параметрическую передаточную функцию. Поэтому необходимо построить серию кривых (рис. 13.7) для различных фиксированных моментов времени, t1, t2, t3 и т. д., а затем через; точки, соответствующие этим значениям времени, провести плавную кривую.

Указанное обстоятельство значительно увеличивает объем вычислительной работы по сравнению с построением кривой переходного процесса в системе с постоянными параметрами.

§ 13.4. Устойчивость и качество регулирования

Для систем с переменными параметрами понятие устойчивости имеет некоторую специфику. Если система работает ограниченный интервал .времени, то понятие асимптотической устойчивости (см. § 6.1) практически теряет свой смысл. Однако для квазистационарных систем при сравнительно медленном изменении коэффициентов

уравнения (13.1) представляется возможным сформулировать понятие устойчивости следующим образом.

Будем считать систему с переменными параметрами устойчивой на заданном интервале времени Т, если ее нормальная функция веса (13.4) или (13.5)

затухает во времени для всех фиксированных значенийυ , лежащих внутри этого интервала. Это условие можно записать следующим образом:

(13.83)

Если для системы получена нормальная функция веса, то вид ее и определяет устойчивость системы.

Однако в некоторых случаях имеется сопряженная функция веса (13.6) или (13.7), которая связана преобразованием Лапласа с параметрической передаточной функцией (13.62) и преобразованием Фурье с параметрической частотной передаточной функцией (13.58) или (13.59). Поэтому более просто можно исследовать вопрос затухания функции веса вдоль аргументов υ (смещение) или θ (реверс-смещение). Условие затухания вдоль этих аргументов можно записать следующим образом:

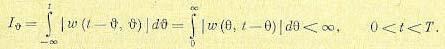(13.84)

Однако затухание сопряженной функции веса и выполнение условия, (13.84) еще не означает затухания нормальной функции веса и выполнения условия (13.83). Заметим, что в системах с постоянными параметрами не наблюдается такой неопределенности, так как для них совпадают оба разреза рельефа функции веса: w(τ) = w(θ) , и оба интеграла:

It = Iυ , определяемые формулами (13.83) и (13.84).

Можно показать [118], что для систем, описываемых дифференциальным уравнением вида

выполнение условия (13.84) практически обеспечивает выполнение условия (13.83). В этих системах исследование устойчивости может быть проведено на базе параметрической передаточной функции.

Исследование затухания сопряженной функции веса может производиться как по ее виду, если она известна для рассматриваемой системы, так и на основании отсутствия полюсов параметрической передаточной функции замкнутой системы в правой полуплоскости и на мнимой оси. Для этой цели .могут привлекаться известные критерии устойчивости, например критерий Михайлова, критерии Найквиста и др.

Формулы главы 5, дающие связь между передаточными функциями замкнутой системы Ф(р), разомкнутой системы W(р) и передаточной функцией по ошибке Фх(р), сохраняют свою силу и для параметрических передаточных функций.

Качество регулирования может быть оценено по виду переходного процесса (переходной функции или функции веса) в соответствии с § 8.4. Для этой цели должны использоваться нормальная функция веса и нормальная переходная функция, определяемые для фиксированного момента времени 0 <υ < Т.

Рассмотрим теперь точность воспроизведения задающего воздействия в следящих системах. Составим дифференциальное уравнение (13.1) так, чтобы в левой части находилась ошибка х(t), а в правой — задающее воздействие g(t):

Реакция системы на дельта-функцию в правой части g(t) =δ(t −υ,υ) представляет собой функцию веса ошибки wx (t −υ,υ) .

В соответствии с формулой (13.11) ошибку системы можно представить в виде

(13.86)

Разлагая задающее воздействие в ряд Тейлора около точки t и подставляя его в (13.86), получаем

(13.87)

Ограничимся случаем, когда t>tп и, где tп — время затухания функции веса. Тогда верхний предел интегрирования в (13.87) можно положить равным бесконечности. В результате (13.87) можно представить в виде

(13.88)

Здесь введено понятие коэффициентов ошибок, определяемых выражением

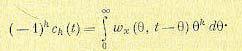(13.89)

В отличие от коэффициентов ошибок системы с постоянными параметрами здесь они получаются зависящими от времени.

Коэффициенты ошибок можно вычислить с помощью параметрической передаточной функции по ошибке Wx ( p,t) . Из (13.62) следует

(13.90)

Дифференцируя Wx ( p,t) по p и положив затем получаем формулу для определения k-го коэффициента:

(13.91)

Коэффициенты ошибок могут быть также получены делением числителя Wx ( p,t) на

знаменатель так, чтобы получить ряд по возрастающим степеням р.

Коэффициенты ошибок могут также определяться для возмущающего воздействия по соответствующей функции веса или по параметрической передаточной функции относительно возмущающего воздействия.

§ 13.5. О синтезе систем с переменными параметрами

Ввиду сложности математического решения синтез систем регулирования с переменными параметрами, как правило, должен осуществляться при помощи вычислительных машин непрерывного или дискретного действия, а также посредством реального моделирования. Вычислительные машины позволяют просмотреть все наиболее важные режимы работы системы, оценить ее качественные показатели и подобрать необходимые корректирующие средства.

Однако во многих случаях, особенно для квазистационарных систем можно провести синтез расчетным путем. Это позволяет более сознательно подойти к определению структуры проектируемой системы и параметров корректирующих средств, что значительно сокращает объем последующих исследований и проверок на вычислительных машинах и моделях.

Метод замороженных коэффициентов. Одним из наиболее простых способов является замораживание переменных во времени параметров в какой-то фиксированный момент

времени t=υ , что ведет к замораживанию коэффициентов дифференциального уравнения (13.1). В этом случае система с переменными параметрами сводится к системе с постоянными параметрами, что позволяет применять для нее известные методы синтеза (см. главу 12).

Разница по сравнению с системами, имеющими постоянные коэффициенты, заключается в том, что исследование системы с замороженными коэффициентами должно быть последовательно проведено для различных моментов: времени t=υ , лежащих в интервале 0 < υ <Т, где Т — время работы системы.

Если во всем рабочем интервале времени от 0 до T качество системы регулирования оказывается приемлемым, то ее считают работоспособной и при изменении коэффициентов уравнения в исследованных пределах.

Этот метод будет давать правильные результаты, если в течение времени переходного процесса (пока функция веса не затухнет практически до нуля) коэффициенты уравнения (13.1) успеют мало изменить свое значение.

Следует заметить, что эффективность рассматриваемого метода может зависеть от правильного выбора фиксированных моментов времени, для которых производится замораживание коэффициентов. Необходимо так выбирать эти моменты времени, чтобы охватить все возможные варианты значений коэффициентов, обратив особое внимание на «опасные» точки, в которых происходит значительное изменение коэффициента, смена его знака и т. п. Безусловно, что правильный выбор рассматриваемых моментов времени во многом зависит от опыта проектировщика.

Метод замороженных реакций. Во многих случаях переменными параметрами обладает не вся система регулирования, а одно из ее звеньев. Чаще всего таким звеном оказывается объект регулирования. Задача синтеза будет сильно упрощена, если звено с переменными параметрами исследовать отдельно, а затем

приближенно заменить его в окрестностях некоторой точки Ф0 эквивалентным звеном с постоянными параметрами. Задача оказывается более простой вследствие того, что в большинстве случаев дифференциальное уравнение звена с переменными параметрами может быть сведено к уравнению первого или второго порядка.

Этот метод оказывается более точным, чем метод замороженных коэффициентов, так как при замене звена с переменными параметрами эквивалентным звеном с постоянными параметрами учитывается факт переменности параметров исходного звена, что будет определять вид и параметры эквивалентного звена.

Идея метода заключается в следующем. Пусть имеется некоторая система регулирования (рис. 13.8), содержащая в своем составе звено с переменными параметрами. Часть системы, соответствующая постоянным параметрам, выделена в отдельное звено.

Для звена с постоянными параметрами может быть определена весовая функция w1 (τ) ,

которая зависит только от времени τ = t −υ (рис. 13.1) и соответствующая ей передаточная функция

(13.92)

Для звена с переменными параметрами определим весовую функцию

w2 (t −υ,υ) = w2 (τ,υ) . Эта весовая функция может быть найдена точно, еcли дифференциальное уравнение звена имеет первый или второй порядок, или

приближенными методами в соответствии с изложенным в § 13.2 и § 13.3. Для ее нахождения могут быть также использованы вычислительные машины с последующей аппроксимацией решения.

После нахождения весовой функции ш2 заморозим ее для некоторого фиксированного момента времени t =υ0 полагая при этом, что весовая функция на небольшом интервале

времени вблизи точки t =υ0 зависит только от времени τ =τ −υ и не зависит от зафиксированного значения смещения. Таким образом, мы получим функцию

(13.93)

Заметим при этом, что мы фиксируем аргумент υ не полностью, а только в той его части, которая делает рельеф функции веса нецилиндрическим. В результате этого оба разреза (рис. 13.2) получаются одинаковыми, т. е. весовые функции (13.5) и (13.7) совпадают.

Для весовой функции (13.93) может быть найдена передаточная функция

(13.94)

Эта передаточная функция по своей сущности является параметрической, так как в нее входит фиксированный параметр доОднако по своим свойствам она полностью совпадает с передаточной функцией звена с постоянными параметрами. Вследствие этого будем называть ее эквивалентной передаточной функцией. С этой передаточной функцией можно в дальнейшем оперировать так, как будто рассматривается звено с постоянными параметрами. В связи с этим рассматриваемую передаточную функцию можно записать сокращенно: W2 ( p,υ0 ) =W2 ( p) .

Однако при этом надо помнить, что исследование системы должно быть произведено при различных значениях фиксированного параметра в пределах 0 < υ0 < Т.

Для системы, изображенной на рис. 13.8, при использовании эквивалентной передаточной функции может быть найдена передаточная функция разомкнутой системы

(13.95)

передаточная функция замкнутой системы

(13.96)

и передаточная функция по ошибке

(13.97)

Эти функции могут быть использованы обычным образом, как это делается для систем с постоянными параметрами при исследовании устойчивости, точности и качества регулирования, но исследование должно охватить весь рабочий интервал υ от 0 до Т. Как и в случае замороженных коэффициентов, здесь приходится намечать «опасные» точки, где должно быть проведено исследование. Однако в рассматриваемом методе можно учитывать при этом не только сами значения коэффициентов в отдельные моменты времени, но и характер их изменения во времени (скорость изменения, ускорение изменения и т. д.). Это делает все исследование более полным при сохранении его относительной простоты. В некоторых случаях оказывается более целесообразным отыскание и последующее замораживание переходной функции звена с переменными параметрами

Для переходной функции (13.18) может быть найдена передаточная функция

(13.99)

По сравнению с нахождением передаточной функции по замороженной весовой функции (13.94) здесь получается обычно более полный учет динамических качеств звена с переменными параметрами. Это оказывается наиболее заметным в тех случаях, когда в правой части дифференциального уравнения звена имеются переменные во времени коэффициенты. Их изменение может быть учтено только при нахождении переходной функции, так как при нахождении весовой функции значения коэффициентов в правой части уравнения; фиксируются в момент приложения единичного импульса.