
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf
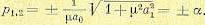 (12.141)
(12.141)
Теперь можно записать выражение для управляемой величины:
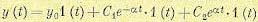 (12.142)
(12.142)
где С1 и С2 — произвольные постоянные. Из начального и конечного условий можно определить, что С1+С2= —у0, а также
Отметим, что принятие более сложного функционала
Пусть теперь в рассматриваемом примере функционал не содержит управляющей величины и имеет, например, вид
не зависит от вида полинома D(р). Подобный результат был получен другим способом ранее в § 8.8, когда экстремаль была решением характеристического уравнения  .
.
Однако при отсутствии ограничений на вид D (р) реализация экстремали (12.148) может привести к физически не осуществимым регуляторам. Действительно, из (12.136) следует, что регулятор должен обеспечить управляющее воздействие вида
 .
.
Однако уже первая производная (12.148) имеет при I = 0 разрыв первого рода, а вторая и следующие производные содержат слагаемые типа δ-функции и ее производных:

Поэтому физическая реализация возможна для степени D (р) не выше первой, но даже и в этом случае регулятор должен быть практически безынерционным.
Получение физически не реализуемого регулятора произошло вследствие отсутствия ограничений или учета управления в принятом функционале качества (12.146). Для получения возможности применения инерционных регуляторов в функционал качества можно вводить кроме управления и его производные. Однако в этом случае смысл функционала качества становится неясным.
Рассмотрим теперь замкнутую систему, у которой объект управления описывается дифференциальным уравнением
 (12.149)
(12.149)
с начальным условием у (0) =y0. Требуется определить оптимальное управление
 , переводящее систему в состояние у = 0 с бесконечным временем регулирования и минимизирующее функционал
, переводящее систему в состояние у = 0 с бесконечным временем регулирования и минимизирующее функционал
и используя уравнения (12.130) или (12.132), а также уравнение объекта {12.149), можно получить характеристическое уравнение замкнутой оптимальной системы в виде
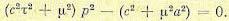 (12.151)
(12.151)
Корень, лежащий в левой полуплоскости,
Уравнение экстремали, проходящей через граничные точки,
из (12.149) можно найти, что |
управление |
должно |
изменяться по закону |
Приняв за неизвестную, |
входящую |
в два |
уравнения (12.152) и (12.153), можно |
записать условие их совместности: |
|
|
|
Отсюда получается уравнение регулятора
 (12.154)
(12.154)
Первое слагаемое в правой части (12.154) соответствует собственно искомому оптимальному закону регулирования
 (12.155)
(12.155)
Второе слагаемое в правой части (12.154) соответствует постоянному значению управления 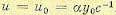 , которое необходимо искусственно создать на выходе регулятора, чтобы в замкнутой системе до момента времени t=0 (т. е. при t < 0) управляемая величина была бы равна заданному значению y0. Как следует из (12.154), при t = 0 это постоянное управление снимается и система начнет приходить в согласованное положение.
, которое необходимо искусственно создать на выходе регулятора, чтобы в замкнутой системе до момента времени t=0 (т. е. при t < 0) управляемая величина была бы равна заданному значению y0. Как следует из (12.154), при t = 0 это постоянное управление снимается и система начнет приходить в согласованное положение.
Если при t < 0 рассматриваемая система была выключена и имела рассогласование у = у0, то слагаемое u0 не нужно и формула (12.154) сводится к (12.155).
Рассмотренный пример относится к так Называемому аналитическому конструированию регуляторов, которое будет изложено более подробно в § 12.10.
§ 12.9. Динамическое программирование
Метод динамического программирования был разработан Р. Беллманом [5]. Он применим не только для решения задач оптимизации систем управления, но и для самых различных технических и экономических задач. При обосновании этого метода предполагается, что функционал качества является дифференцируемой функцией фазовых координат системы. Заметим, что это условие выполняется не всегда.
Пусть система описывается совокупностью п уравнений, записанных для фазовых координат;
 (12.156)
(12.156)
где fi — некоторые, в общем случае нелинейные функции фазовых координат и управлений. Число последних для общности принято равным числу фазовых координат.
Уравнения (12.156) можно представить также в матричной форме:
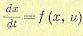 (12.157)
(12.157)
где х и u — матрицы-столбцы фазовых координат и управлений размером 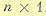 . В качестве критерия оптимальности примем минимум функционала
. В качестве критерия оптимальности примем минимум функционала
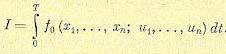 (12.158)
(12.158)
Функции f0 и ft, вообще говоря, могут содержать в явном виде текущее время t. Однако это не меняет принципиальной постановки задачи.
Целью управления является перевод системы из состояния  при t=0 в состояние
при t=0 в состояние
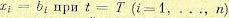 . Такая задача управления называется терминальной, и она соответствует определению в фазовом пространстве оптимальной траектории с закрепленными концами.
. Такая задача управления называется терминальной, и она соответствует определению в фазовом пространстве оптимальной траектории с закрепленными концами.
Будем считать, что фазовые координаты и управления должны принадлежать некоторым замкнутым (ограниченным) пространствам, т. е.
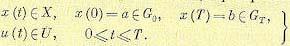 (12.159)
(12.159)
Можно несколько расширить цель управления и считать, что конец траектории должен
только находиться в заданной области 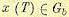 при t =-Т. Это будет задача со свободным концом траектории.
при t =-Т. Это будет задача со свободным концом траектории.
Вместо исходной можно решать более общую задачу отыскания оптимального управления для произвольной временной точки 0 < t0 < Т и произвольной точки в фазовом пространстве
 в смысле минимума функционала
в смысле минимума функционала
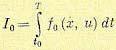 (12.160 )
(12.160 )
Минимум функционала (12.160) зависит от начального момента времени tо и начальной
точки х0 = х (t0). Обозначим этот минимум через 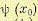 . Функция
. Функция 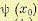 для некоторой совокупности фазовых координат x(t0) может, вообще говоря, не существовать, так как может не существовать допустимого управления, удовлетворяющего (12.156).
для некоторой совокупности фазовых координат x(t0) может, вообще говоря, не существовать, так как может не существовать допустимого управления, удовлетворяющего (12.156).
Если найдены функция 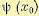 и требуемое управление u (t, х0), то, положив
и требуемое управление u (t, х0), то, положив 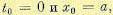 , где а — матрица-столбец начальных условий, мы получим решение исходной задачи.
, где а — матрица-столбец начальных условий, мы получим решение исходной задачи.
Принцип оптимальности. Примем начальные условия: при 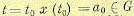 , оптимальное управление u (t, а0) реализует минимум функционала (12.160), а х (t, а0) — оптимальная траектория в фазовом пространстве. Выберем произвольный момент времени t1, принадлежащий интервалу t0 — Т, и обозначим через а1 точку
, оптимальное управление u (t, а0) реализует минимум функционала (12.160), а х (t, а0) — оптимальная траектория в фазовом пространстве. Выберем произвольный момент времени t1, принадлежащий интервалу t0 — Т, и обозначим через а1 точку 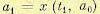 на оптимальной траектории
на оптимальной траектории 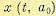 . Принцип оптимальности гласит следующее.
. Принцип оптимальности гласит следующее.
Если принять значения 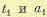 за начальные, то на интервале
за начальные, то на интервале  оптимальное управление
оптимальное управление 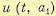 совпадет с оптимальным управлением
совпадет с оптимальным управлением 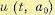 и, следовательно, участок
и, следовательно, участок
оптимальной траектории  для задачи с начальной точкой (t0, а0) на интервале
для задачи с начальной точкой (t0, а0) на интервале  совпадет с оптимальной траекторией для задачи с начальной точкой
совпадет с оптимальной траекторией для задачи с начальной точкой  . Доказательство достаточно очевидно. Оно исходит из того, что значение функционала качества на участке t1—Т должно быть одинаковым при управлениях u(t, а1) и u(t, а0). Если бы это было не так и значение функционала на этом интервале времени было бы, например, меньше для управления u(t, а1), то управление u(t, а0) можно было бы улучшить, заменив его на интервале t1—Т управлением
. Доказательство достаточно очевидно. Оно исходит из того, что значение функционала качества на участке t1—Т должно быть одинаковым при управлениях u(t, а1) и u(t, а0). Если бы это было не так и значение функционала на этом интервале времени было бы, например, меньше для управления u(t, а1), то управление u(t, а0) можно было бы улучшить, заменив его на интервале t1—Т управлением  , что противоречит принятому предположению об оптимальности управления
, что противоречит принятому предположению об оптимальности управления 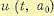 .
.
Итак, в соответствии с изложенным введем функциональное уравнение
 (12.161)
(12.161)
на основании которого может быть найдено оптимальное управление и (х). Если на промежутке t0 — Т выбрать промежуточную точку t1, то на основании принципа оптимальности
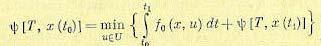 (12.162)
(12.162)
Функция 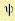 и оптимальное управление обычно не могут быть найдены аналитическим путем. Для этой цели применяются приближенные методы с использованием вычислительных машин. Рассмотрим идею приближенного расчета.
и оптимальное управление обычно не могут быть найдены аналитическим путем. Для этой цели применяются приближенные методы с использованием вычислительных машин. Рассмотрим идею приближенного расчета.
Пусть t — фиксированное значение времени, а  — малый отрезок времени, причем
— малый отрезок времени, причем  . Тогда
. Тогда
 (12.163)
(12.163)
где функции  связаны условиями (12.157).
связаны условиями (12.157).
Вид управления 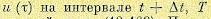 не оказывает влияния на первое слагаемое в правой части (12.163). Поэтому на рассматриваемом интервале времени следует так выбрать управление, чтобы минимизировать второе слагаемое в правой части (12.163) при выполнении условий
не оказывает влияния на первое слагаемое в правой части (12.163). Поэтому на рассматриваемом интервале времени следует так выбрать управление, чтобы минимизировать второе слагаемое в правой части (12.163) при выполнении условий
 (12.164)
(12.164)
На основании принципа оптимальности перепишем (12.163) следующим образом:
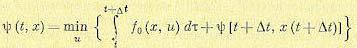 (12.165)
(12.165)
На интервале 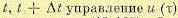 должно быть выбрано так, чтобы минимизировать правую часть (12.165). От этого выбора зависят оба слагаемых правой части.
должно быть выбрано так, чтобы минимизировать правую часть (12.165). От этого выбора зависят оба слагаемых правой части.
Заменим на малом интервале 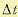 матричную функцию f(х, u) и функцию fо (х, u) их фиксированными значениями в точке t, а производную
матричную функцию f(х, u) и функцию fо (х, u) их фиксированными значениями в точке t, а производную 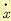 отношением конечных разностей
отношением конечных разностей
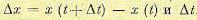 . Тогда вместо (12.165) можно записать приближенно
. Тогда вместо (12.165) можно записать приближенно
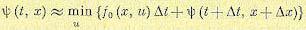 (12.166)
(12.166)
Кроме того, имеем
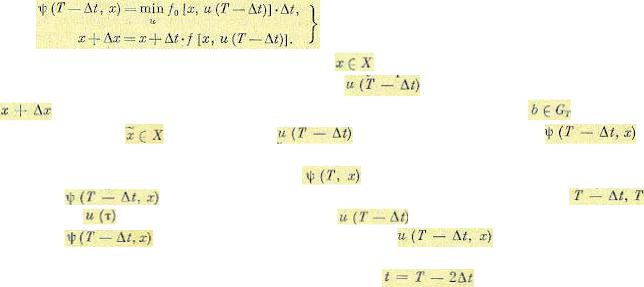
 (12.167)
(12.167)
На основании (12.166) и (12.167) можно найти приближенное значение 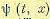 . Для
. Для
конечного момента времени Т и любых  следует, что
следует, что  . Поэтому вычисление
. Поэтому вычисление 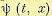 удобно начинать с конца, т. е. с момента времени t=Т и области GT. На первом шаге
удобно начинать с конца, т. е. с момента времени t=Т и области GT. На первом шаге
расчета рассматривается момент времени 
вследствие краевого условия принадлежит множеству Gт. Подставляя в (12.166) и (12.167) значение  и учитывая, что
и учитывая, что  , имеем
, имеем
|
|
(12.168) |
|
|
|
Далее фиксируется произвольное значение |
. Минимум правой части первого |
||||
равенства (12.168) вычисляется по тем значениям |
|
из множества U, для которых точка |
|||
, определяемая вторым равенством (12.168), соответствует значению |
. Если для |
||||
какой-либо точки |
таких значений |
не существует, то функция |
не |
||
определена в точке х. |
|
|
|
||
Таким образом, по значению функции |
можно приближенно определить значения |
||||
функции |
|
на некотором подмножестве Х1 из X. Так как на интервале |
|
||
управление |
|
принято постоянным и равным |
|
, то одновременно с нахождением |
|
функции |
|
приближенно найдено управление |
, которое реализует эту |
||
функцию. |
' |
|
|
|
|
На втором шаге рассматривается момент времени |
. Из (12.166) и (12.167) |
||||
можно получить |
|
|
|
|
|
 (12.169)
(12.169)
Далее фиксируется произвольная точка  . Минимум правой части (12.169) вычисляется по тем значениям
. Минимум правой части (12.169) вычисляется по тем значениям 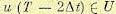 , для которых точка
, для которых точка  , определяемая вторым равенством (12.169), принадлежит подмножеству Х1. Находится значение функции
, определяемая вторым равенством (12.169), принадлежит подмножеству Х1. Находится значение функции 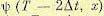 на некотором подмножестве Х2 из Х1. На интервале
на некотором подмножестве Х2 из Х1. На интервале  управление
управление
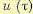 принимается постоянным и равным значению
принимается постоянным и равным значению  , реализующим
, реализующим 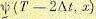 . На интервале
. На интервале 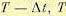 управление, как функция
управление, как функция  , было определено после первого шага. Так как
, было определено после первого шага. Так как  связано с
связано с  вторым равенством (12.169), то после двух шагов оказывается определенным управление
вторым равенством (12.169), то после двух шагов оказывается определенным управление  на интервале времени
на интервале времени 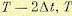 . Это будет кусочно-постоянная функция с интервалами постоянства, равными
. Это будет кусочно-постоянная функция с интервалами постоянства, равными 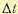 .
.
Последующие шаги рассчитываются аналогично. Если весь интервал управления Т разбит на m шагов, то после m-го шага определяется функция 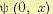 на подмножестве Хm из X и управление u (0, х), как кусочно-постоянная функция с интервалами постоянства
на подмножестве Хm из X и управление u (0, х), как кусочно-постоянная функция с интервалами постоянства 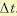 . Если начальная точка х (0) = а принадлежит подмножеству Хm, для которого определена функция
. Если начальная точка х (0) = а принадлежит подмножеству Хm, для которого определена функция
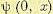 , то, положив х = а, получаем
, то, положив х = а, получаем  — минимум функционала (12.161) исходной задачи управления и
— минимум функционала (12.161) исходной задачи управления и  — оптимальное управление. Подставляя затем оптимальное управление в (12.156) или (12.157) и решая систему исходных дифференциальных
— оптимальное управление. Подставляя затем оптимальное управление в (12.156) или (12.157) и решая систему исходных дифференциальных
уравнений, можно определить оптимальную траекторию движения  .
.
Если х (0) = а не принадлежит подмножеству Хm, то задача не имеет решения. Надо учитывать при этом, что вся задача решалась приближенно, в том числе найдено было приближенно и подмножество Хm.
При использовании динамического программирования число шагов должно быть достаточно большим, чтобы получить приемлемую точность решения. В результате большой трудоемкости использование этого метода оказывается невозможным без применения вычислительных машин.
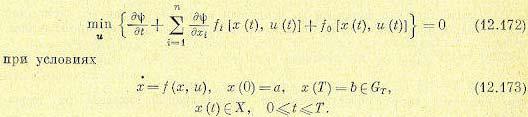
Серьезным недостатком метода является то, что с ростом размерности задачи (порядка n дифференциального уравнения) весьма серьезно возрастают требования к быстродействию и объему памяти вычислительных машин. Действительно, на k-м шаге вычисляется функция
 , зависящая от переменных
, зависящая от переменных  и определенная на множестве Хk. Ее надо
и определенная на множестве Хk. Ее надо
хранить в памяти машины до тех пор, пока не будет вычислена функция 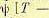
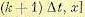 . Это значит, что в памяти машины должна храниться таблица, в которой записаны значения
. Это значит, что в памяти машины должна храниться таблица, в которой записаны значения
 для различных точек из Хk. Этих точек оказывается много, так как таблица должна достаточно точно и равномерно определять функцию
для различных точек из Хk. Этих точек оказывается много, так как таблица должна достаточно точно и равномерно определять функцию  . Кроме того, в памяти машины приходится запоминать кусочно-постоянную в общем случае «-мерную
. Кроме того, в памяти машины приходится запоминать кусочно-постоянную в общем случае «-мерную
функцию управления 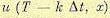 , зависящую от х1, . . ., хn и вычисленную при значениях аргумента т с интервалом
, зависящую от х1, . . ., хn и вычисленную при значениях аргумента т с интервалом  .
.
В сложных системах объем вычислительных операций при реализации приближенного решения задачи динамического программирования оказывается непосильным даже для самых крупных и быстродействующих современных вычислительных машин.
Уравнение Беллмана. Введем предположение, что функция  имеет непрерывные частные производные по всем своим аргументам:
имеет непрерывные частные производные по всем своим аргументам:  . Тогда в равенстве (12.166) функцию
. Тогда в равенстве (12.166) функцию  можно представить следующим образом:
можно представить следующим образом:
 (12.170)
(12.170)
Здесь  — величина более высокого порядка малости, чем
— величина более высокого порядка малости, чем  Входящие в правую
Входящие в правую
часть (12.170) производные  удовлетворяют (12.156). Поэтому
удовлетворяют (12.156). Поэтому
 (12.171)
(12.171)
Подставим (12.171) в (12.166). Функция 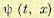 не зависит от управления u(t) в момент t. Поэтому ее можно вынести за знак минимума. Деля полученное равенство на
не зависит от управления u(t) в момент t. Поэтому ее можно вынести за знак минимума. Деля полученное равенство на 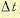 и переходя к пределу при
и переходя к пределу при  , имеем
, имеем
Уравнение (12.172) и представляет собой уравнение Беллмана с краевым условием  . Сумма первых двух членов (12.172) есть полная производная функции
. Сумма первых двух членов (12.172) есть полная производная функции  по времени. Поэтому уравнение Беллмана можно записать в другом виде:
по времени. Поэтому уравнение Беллмана можно записать в другом виде:
 (12.174)
(12.174)
Требование непрерывной дифференцируемости функции 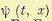 является весьма жестким и во многих задачах не выполняется. В. Г. Болтянский показал [18], что можно ослабить требования к функции
является весьма жестким и во многих задачах не выполняется. В. Г. Болтянский показал [18], что можно ослабить требования к функции  . В ней допускаются разрывы частных производных на некотором множестве точек.
. В ней допускаются разрывы частных производных на некотором множестве точек.
Заметим, что если функции 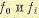 , не зависят явно от времени, то решение уравнения (12.174) — функция
, не зависят явно от времени, то решение уравнения (12.174) — функция 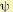 и оптимальное управление u, которое реализует минимум в (12.174), тоже
и оптимальное управление u, которое реализует минимум в (12.174), тоже
не зависит явно от времени, т. е.  и u = u (х), однако в общем случае
и u = u (х), однако в общем случае
 .
.
Аналитическое нахождение функции т|з в явной форме удается только в некоторых частных случаях. Один из таких случаев рассмотрен в следующем параграфе.

 (12.182)
(12.182)
В левой части (12.182) находится квадратичная форма переменных х1,...,хn- Она будет тождественно равна нулю при равенстве нулю всех ее коэффициентов:
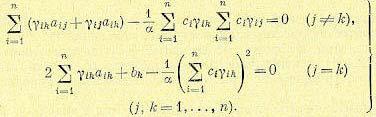 (12.183)
(12.183)
В результате получена система из 0,5n(n+1) алгебраических уравнений, содержащих такое
же количество неизвестных 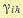 (при учете равенства коэффициентов
(при учете равенства коэффициентов  )
)
После нахождения неизвестных коэффициентов -угь из (12.178) можно определить оптимальное управление
 (12.184)
(12.184)
Аналогичный результат может быть получен при использовании классических методов вариационного исчисления (§ 12.8).
Решение обратной задачи. В полученных формулах для оптимального управления конструктору -необходимо формировать управление в функции всех фазовых координат, так как
в (12.184) все коэффициенты  .
.
Если конструктор может использовать ограниченное число фазовых координат, то часть коэффициентов dk в (12.184) должна быть тождественно равна нулю. В этом случае для формирования оптимального управления можно воспользоваться решением обратной задачи и отыскать допустимую форму функционала качества при неполном управлении. Для этого функционал качества (12.176) представим в измененном виде:
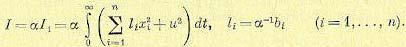 (12.185)
(12.185)
Минимизация функционала I1 вместо I не меняет задачи.
Будем считать отличные от нуля коэффициенты dk известными числами, а коэффициенты li
— неизвестными. Тогда совокупность уравнений (12.183) может быть представлена в виде
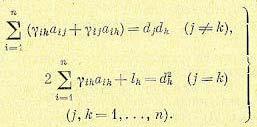 (12.186)
(12.186)
Эта система содержит 0,5n (n+1) неизвестных коэффициентов  и n неизвестных коэффициентов функционала I1. Добавляя к уравнениям (12.186) n уравнений из (12.184)
и n неизвестных коэффициентов функционала I1. Добавляя к уравнениям (12.186) n уравнений из (12.184)
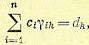 (12.187)
(12.187)
получим систему уравнений, которая в принципе может быть разрешена относительно искомых неизвестных. Если система уравнений (12.186) и (12.187) имеет решение, при котором коэффициенты 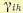 удовлетворяют критерию Сильвестра (12.181), а коэффициенты функционала
удовлетворяют критерию Сильвестра (12.181), а коэффициенты функционала
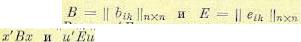
lk>0, то задача аналитического конструирования при заданном неполном управлении имеет смысл.
Так как коэффициенты функционала получаются в виде lk = 1k (d1; ... . . ., dn), то найденный ответ дает и решение прямой задачи. Варьируя коэффициенты управления dk в пределах,
допускаемых условиями Сильвестра и условиями  , можно выбрать подходящий критерий качества и оптимальное управление.
, можно выбрать подходящий критерий качества и оптимальное управление.
Методика обратного решения аналитического конструирования может оказаться полезной и при возможности использования полного управления (в функции всех фазовых координат). Это объясняется тем, что система уравнений (12.186) и (12.187) оказывается линейной относительно
коэффициентов  и решается проще, чем система уравнений (12.183), которая нелинейна
и решается проще, чем система уравнений (12.183), которая нелинейна
относительно искомых коэффициентов 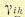 .
.
Векторное управление. В работах В. И. Зубова [46] рассматривается более общая задача, когда дан нестационарный объект, описываемый матричным уравнением
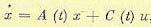 (12.188)
(12.188)
где А (t) и С, (t) — квадратные матрицы коэффициентов 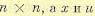 — матрицы-столбцы фазовых координат и управлений. Вводится квадратичный функционал вида
— матрицы-столбцы фазовых координат и управлений. Вводится квадратичный функционал вида
 (12.189)
(12.189)
где |
— заданные квадратные матрицы, а |
— положительно |
определенные квадратичные формы. Решение задачи сводится |
к линейному управлению вида |
|
 (12.190)
(12.190)
Матрица Г определяется решением нелинейного матричного уравнения
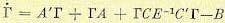 (12.191)
(12.191)
Для стационарных объектов матрицы А к С не зависят от времени и уравнение (12.191) принимает вид
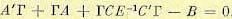 (12.192)
(12.192)
В большинстве случаев результаты, полученные при аналитическом конструировании регуляторов, не могут быть реализованы точно вследствие необходимости использовать для управления все фазовые координаты. Поэтому приходится говорить лишь о приближенной реализации полученных условий оптимальности. Другие подходы к проблеме аналитического конструирования регуляторов содержатся в работах [46, 60, 62, 77, 133].
РАЗДЕЛ III ОСОБЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
ГЛАВА 13 СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
§ 13.1. Основные понятия
Линейными системами с переменными параметрами называются системы, движение которых описывается линейными дифференциальными уравнениями временными во времени коэффициентами:
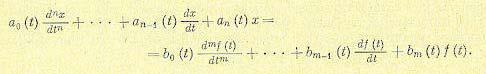 (13.1)
(13.1)
Коэффициенты а0, . . ., аn и b0, . . ., bm являются функциями времени, которые задаются либо графиками, построенными на основании эксперимента, либо аналитически.
Переменные коэффициенты |
в уравнении системы |
автоматического регулирования |
|
(13.1) возникают |
вследствие |
наличия переменных |
коэффициентов хотя бы в одном |
звене системы. Так, |
например, |
у подвижного объекта (корабля, самолета, ракеты) с |
|
течением времени вследствие выгорания топлива происходит изменение массы и моментов инерции. Если объект при своем движении меняет скорость и высоту, то возможно изменение его аэродинамических коэффициентов.
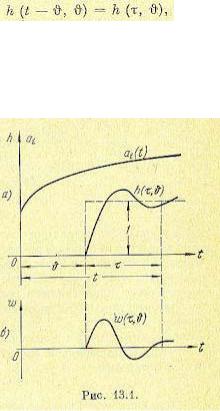
Рассмотрим переходную функцию и функцию веса системы с переменными параметрами. Так как коэффициенты уравнения (13.1) меняются с течением времени, то эти функции будут зависеть от момента приложения единичного скачка или единичного импульса на входе. На рис. 13.1, а изображен график изменения одного из коэффициентов уравнения (13.1) и переходная функция
(13.2)
где t — текущее время, отсчитываемое от некоторого момента, соответствующего, например, включению системы регулирования или началу изменения переменных параметров; ϑ — время, соответствующее поступлению на вход единичной ступенчатой функции; τ — текущее время, отсчитываемое от момента приложения ступенчатой функции.

 (12.175)
(12.175) — матрица-столбец фазовых координат,
— матрица-столбец фазовых координат,  — квадратная
— квадратная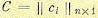 — матрица-столбец коэффициентов, u — скаляр. Требуется определить оптимальное управление
— матрица-столбец коэффициентов, u — скаляр. Требуется определить оптимальное управление 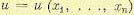 , минимизирующее функционал качества
, минимизирующее функционал качества (12.176)
(12.176) в конечное
в конечное 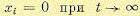 . Из формулировки задачи следует, что система должна быть при этом асимптотически устойчива.
. Из формулировки задачи следует, что система должна быть при этом асимптотически устойчива. (12.177)
(12.177)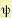 , входящая в (12.177), является функцией Ляпунова, а функция V в функционале (12.176) — ее полной производной, т. е.
, входящая в (12.177), является функцией Ляпунова, а функция V в функционале (12.176) — ее полной производной, т. е. . Будем искать решение этого уравнения в виде квадратичной формы от фазовых координат:
. Будем искать решение этого уравнения в виде квадратичной формы от фазовых координат: (12.180)
(12.180)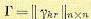 — квадратная матрица коэффициентов, удовлетворяющая критерию Сильвестра
— квадратная матрица коэффициентов, удовлетворяющая критерию Сильвестра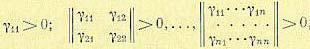 (12.181)
(12.181) - Функция (12.180) удовлетворяет граничному условию, так как при х
- Функция (12.180) удовлетворяет граничному условию, так как при х .
.