
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf
Демпфирование с введением отрицательных фазовых сдвигов. Сущность этого метода можно уяснить, например, из рассмотрения рис. 6.22. На рис. 6.22, б изображен случай, когда изза наличия в канале разомкнутой системы консервативного звена, имеющего чисто мнимые полюсы, замкнутая система будет неустойчивой. Добавление отрицательного фазового сдвига вызовет «закручивание» а. ф. х. по часовой стрелке. В результате система в замкнутом состоянии может быть сделана усхойчивой (рис. 6.22, а).
Введение отрицательного фазового сдвига производится использованием последовательных корректирующих звеньев фазосдвигающего типа (табл. 10.1). Так как подобные звенья оказываются обычно неминимально-фазовыми, то такой метод демпфирования иногда называют в литературе методом демпфирования с использованием неминимально-фазовых звеньев. Демпфирование с введением отрицательных фазовых сдвигов оказывается эффективным в случае наличия в канале разомкнутой системы консервативных, а также колебательных звеньев со слабым демпфированием. В первом случае это приводит к появлению в амплитудной частотной характеристике (или в л. а. х.) резонансных пиков бесконечной высоты, а во втором — к резонансным пикам конечной, но значительной высоты. Использование демпфирования других типов здесь оказывается затруднительным.
По своим свойствам этох метод демпфирования сходен со случаем подавления средних частот, так как фазосдвигающие звенья обычно не вносят изменений в амплитудную частотную характеристику и модуль их частотной передаточной функции  . В результате сохраняется быстродействие демпфируемой системы и сохраняется ее полоса пропускания. Рассмотренные выше методы демпфирования систем регулирования являются основными, но лишь иллюстрируют те идеи, которые используются для повышения запаса устойчивости. В практике, в зависимости от конкретных условий, могут использоваться и более сложные изменения динамических свойств системы регулирования. Так, например, может осуществляться подавление средних частот с одновременным поднятием высоких, поднятие высоких частот с подавлением их некоторой области (фильтрация определенных частот) и т. п.
. В результате сохраняется быстродействие демпфируемой системы и сохраняется ее полоса пропускания. Рассмотренные выше методы демпфирования систем регулирования являются основными, но лишь иллюстрируют те идеи, которые используются для повышения запаса устойчивости. В практике, в зависимости от конкретных условий, могут использоваться и более сложные изменения динамических свойств системы регулирования. Так, например, может осуществляться подавление средних частот с одновременным поднятием высоких, поднятие высоких частот с подавлением их некоторой области (фильтрация определенных частот) и т. п.
§10.6. Примеры
1.Система управления движущимся объектом. Рассмотрим систему управления, изображенную на рис. 10.18. Здесь обозначено: ГН — гироскоп
направления, показывающий отклонение движущегося объекта от заданного курса; П — потенциометр; Д — двигатель рулевого устройства и Р — редуктор. При отклонении объекта от заданного курса на угол α ее движок потенциометра отклоняется на тот же угол. В результате на усилитель поступает напряжение. Пройдя усилитель, это напряжение поступает на двигатель, и руль объекта начинает поворачиваться.
Составим передаточную функцию разомкнутой системы. Для этой цели отсоединим гироскоп направления от объекта и введем обозначения: а1 — угол отклонения гироскопа и а2 — угол поворота объекта (в замкнутой системе а1 = а2 = а).
Передаточная функция разомкнутой системы
Найдем передаточные функции отдельных звеньев.
Потенциометр. Считая потенциометр безынерционным звеном, получаем
 (10.47)
(10.47)
где k1 — крутизна потенциометра  Усилитель. При безынерционном усилителе
Усилитель. При безынерционном усилителе


где постоянная времени  Передаточная функция разомкнутой системы
Передаточная функция разомкнутой системы
 (10.55)
(10.55)
Характеристическое уравнение системы (10.72) в этом случае уже не имеет пропуска членов:
 (10.56)
(10.56)
и при соответствующем выборе постоянной времени коррекции Тк и общего коэффициента усиления в системе может быть получена устойчивая работа. 2. Следящая система. Схема следящей системы без корректирующих средств изображена на рис. 6.4. В этом случае предельная добротность по скорости из условия устойчивости определяется неравенством, полученным в § 6.2:
Рассмотрим случай демпфирования с поднятием верхних частот. Включим последовательно в канал усиления (рис. 10.21) пассивное дифференцирующее звено ПЗ с передаточной функцией
 (10.57)
(10.57)
где 
Будем считать, что затухание G0 вносимое звеном на низких частотах, компенсируется соответствующим увеличением коэффициента усиления
усилителя. Тогда передаточная функция разомкнутой системы, полученная в § 6.2:
примет вид
 (10.58)
(10.58)
Примем теперь, что в использованном пассивном звене выполнено условие Т1=ТМ. Тогда вместо (10.58) получим
 (10.59)
(10.59)
Найдем характеристическое уравнение
Подстановка выражения для передаточной функции (10.59) приводит к уравнению
 (10.60)
(10.60)
Условие устойчивости
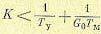 (10.61)
(10.61)
Нетрудно видеть, что, уменьшая коэффициент G0 можно получить устойчивость при любом значении добротности следящей системы.
Рассмотрим теперь случай демпфирования с подавлением средних частот той же следящей системы (см. рис. 6.4). Для этой цели охватим часть усилителя, содержащую инерционность, гибкой отрицательной обратной связью (рис. 10.22, а). Согласно табл. 10.4 это эквивалентно

включению последовательного интегро-дифференцирующего звена, обладающего свойством подавлять средние частоты.
Передаточная функция разомкнутой системы может быть получена из передаточной функции исходной системы делением ее на 
представляет собой передаточную функцию по петле обратной местной связи
Здесь kс — коэффициент усиления части усилителя, охваченной обратной связью, Т = RC — постоянная времени дифференцирующего конденсатора в цепи обратной связи.
В результате получим
 (10.63)
(10.63)
Положим теперь, что выполняется условие T=Tм. Это всегда легко сделать выбором параметров R и С. Тогда
 (10.64)
(10.64)
характеристическое уравнение
 (10.65)
(10.65)
условие устойчивости
 (10.66)
(10.66)
Из этого неравенства видно, что введение обратной связи1 позволяет повысить добротность системы К по сравнению со случаем kс = 0.
Вместо включения гибкой отрицательной обратной связи аналогичный эффект может быть достигнут введением в прямую цепь эквивалентного пассивного интегро-дифференцирующего звена (рис. 10.22, б).

ГЛАВА 11 СЛУЧАЙНЫЕ ПРОЦЕССЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ
§ 11.1. Вводные замечания
До сих пор поведение систем автоматического регулирования исследовалось при определенных, заданных во времени задающих и возмущающих воздействиях (ступенчатая функция, импульсная функция, гармоническое воздействие и т. д.).
Однако во многих случаях характер воздействия бывает таким, что его нельзя считать определенной функцией времени. Оно может принимать с течением времени самые разнообразные случайные значения. В таких случаях мы можем оценить только вероятность появления той или иной формы воздействия в тот или иной момент времени. Это происходит не потому, что оно неизвестно заранее, а потому, что сама природа реального задающего или возмущающего воздействия такова, что величина его в каждый момент времени и процесс его изменения с течением времени зависят от множества разнообразных величин, которые случайным образом могут комбинироваться друг с другом, появляться одновременно или с любым сдвигом во времени и т. д.
Возьмем, например, систему автоматического регулирования напряжения электрического генератора. Возмущающее воздействие здесь является результатом изменения нагрузки в сети, зависящей от включения, выключения и изменения режима работы множества потребителей электрической энергии.
Другой пример — автопилот. На него Действуют обычно возмущающие воздействия случайного характера: порывы ветра и изменения других атмосферных факторов, изменение тяги, изменения напряжения питания усилителей и рулевых машинок и т. д.
Третий пример — следящие системы, на вход которых попадают вместе с полезным сигналом помехи. Например, в радиолокационной системе сопровождения отраженный от цели сигнал содержит в себе помехи в виде многочисленных флуктуации, происходящих от вибраций и поворотов цели, замирания сигнала и т. п.
Аналогичные помехи случайной природы имеют место в других автоматических устройствах.
В следящих системах не только возмущающие воздействия и помехи являются случайными, но и сам полезный сигнал, который должен воспроизводиться (задающее воздействие), как правило, носит случайный характер.
Прежде чем рассматривать поведение автоматических систем при случайных воздействиях, напомним некоторые сведения о случайных величинах, случайных процессах и об их вероятностных характеристиках.
К категории случайных событий можно отнести такие, точное предсказание протекания которых в каждом отдельном случае оказывается невозможным.
Так, например, если бросать монету, то выпадение герба или цифры будет случайным событием. Если повторить этот эксперимент N раз, то можно зафиксировать определенное число
выпадений герба m и число выпадений цифры N — m. Относительная величина  называется
называется
частотой события выпадения герба, а величина |
— частотой события выпадения цифры. |
 -
-
Если устремить число экспериментов  , то частоты событий будут стремиться к некоторому пределу
, то частоты событий будут стремиться к некоторому пределу

 (11.1)
(11.1)
называемому вероятностью данного события. В рассмотренном случае очевидно, что обе вероятности выпадения герба и цифры одинаковы и равны 0,5.
Вероятность каждого события лежит в интервале .
.
Если событие является невозможным, вероятность его равна нулю; если событие является достоверным, его вероятность равна единице.
В примере с бросанием монеты рассматривалась дискретная случайная величина, которая могла принимать два фиксированных значения — выпадение герба и выпадение цифры. Существуют случайные величины, которые могут принимать непрерывные значения. Так, например, если рассмотреть стрельбу из орудия (рис. 11.1), то расстояние L от орудия до места падения снаряда будет случайной величиной, которая на определенном отрезке может принимать все возможные значения. В этом случае можно говорить о вероятности нахождения случайной величины L ъ некотором интервале от L1 до L2.
Вероятностные характеристики дискретных случайных величин. Чтобы полностью знать дискретную случайную величину, надо иметь следующие данные:
а) все возможные значения, которые она может принимать при данных условиях задачи или опыта;
б) вероятность появления каждого из этих значений.
Так, например, если дискретная случайная величина может принимать конечное число значений х1, х2, х3, . . ., хn и вероятность каждого значения будет соответственно Р1; Р2, РЗ, ..., Рn то можно представить так называемый закон распределения случайной величины в виде таблицы 11.1.
При этом должно выполняться условие
 (11.2)
(11.2)
Пусть, например, производится опыт бросания игральной кости. Очевидно, что при каждом бросании число выпавших очков, которое представляет собой случайную величину, может принимать одно из следующих значений: 1, 2, 3, 4, 5, 6. Если кость совершенно симметрична, то вероятность выпадения каждой из этих цифр является одинаковой. Так как число различных значений, которое может принимать случайная величина, равно шести, то из (11.2) имеем
Графически этот закон распределения изображен на рис. 11.2. Он представляет собой равновероятное распределение в некотором интервале (в рассматриваемом случае от 1 до 6).
В некоторых случаях закон распределения случайной величины может задаваться в аналитической форме.

Примером аналитического задания закона распределения дискретной случайной величины является часто используемый закон Пуассона. Он применим к дискретным случайным величинам, которые теоретически могут принимать все положительные значения от 0 до оо. Примерами таких величин могут служить число пассажиров вагона трамвая, число вызовов на телефонной станции в течение какого-либо определенного отрезка времени, число электронов, попадающих на анод электронной лампы за определенный промежуток времени, и т. п. Этот закон записывается следующим образом для целых значений числа х:
где Р (x) — вероятность появления значения х; λ представляет собой среднее значение данной дискретной величины, полученное по результатам большого числа опытов.
Графически этот закон имеет вид, изображенный на рис. 11.3, причем место максимума зависит от величины λ.
В качестве одного из примеров рассмотрим функцию у (t), которая может принимать одно из значений + а или — а (рис. 11.4).
Предположим, что среднее число перемен знака в единицу времени этой функции равно \и и что вероятность перемены знака на интервале 
не зависит от того, что происходит в остальные моменты времени. Тогда вероятность перемены знака на интервале ∆t составит  . Вероятность того, что на интервале ∆t не произойдет
. Вероятность того, что на интервале ∆t не произойдет
перемены знака, будет  .
.
Если взять два интервала времени ∆t, то вероятность отсутствия перемены знака на двух интервалах будет равна произведению вероятностей и составит  . Для трех
. Для трех
интервалов ∆t она составит  ит.д.
ит.д.
Возьмем теперь конечный интервал времени Т, который можно представить в виде
 . Тогда вероятность отсутствия перемены знака на этом интервале можно найти из выражения
. Тогда вероятность отсутствия перемены знака на этом интервале можно найти из выражения
Аналогичным образом можно показать, что вероятность одной перемены знака на
интервале Т будет  , вероятность двух перемен знака
, вероятность двух перемен знака  и т. д. Следовательно, вероятность х перемен знака на интервале времени Т будет определяться выражением
и т. д. Следовательно, вероятность х перемен знака на интервале времени Т будет определяться выражением
 (11.4)
(11.4)

которое совпадает с формулой (11.3), если положить в ней  , где
, где  — среднее число перемен знака на интервале времени Т, которое будет наблюдаться при многократном повторении наблюдения.
— среднее число перемен знака на интервале времени Т, которое будет наблюдаться при многократном повторении наблюдения.
Хотя закон распределения полностью определяет случайную величину, для практики нужны некоторые более простые осредненные характеристики случайной величины, выражающиеся в виде обыкновенных неслучайных чисел.
Одной из таких характеристик является среднее значение, или математическое ожидание, случайной величины. Оно определяется из выражения
 (11.5)
(11.5)
Так, например, для случая бросания игральной кости
Вообще для равновероятного закона распределения (11.5) превращается в формулу
Для случайной величины, распределенной по закону Пуассона, среднее значение, подсчитанное по формуле (11.5), дает
Основные свойства среднего значения случайной величины следующие.
1.Для любых случайных величин среднее значение их суммы равно сумме средних значений этих величин:
2.Среднее значение произведения случайных величин, независимых друг от друга, равно произведению средних значений этих величин:
Последняя формула не распространяется на общий случай любых случайных величин. В виде обобщения понятия среднего значения (11.5) отметим, что выражение
 (11.6)
(11.6)
называется моментом m-го порядка случайной величины х. В частности, момент нулевого порядка выражает свойство (11.2), и он всегда равен единице:
Момент первого порядка есть среднее значение (математическое ожидание) случайной величины (11.5). Момент второго порядка
есть средний квадрат случайной величины.
Часто используется так называемое среднеквадратичное значение случайной величины, представляющее собой корень квадратный из среднего квадрата случайной величины:
Иногда рассматривается центрированное значение случайной величины 
— среднее значение. Тогда аналогично формуле (11.6). можно ввести, понятие центрального момента m-то порядка
 (11.7)
(11.7)
Из формулы (11.7) следует, что центральный момент первого порядка всегда равен нулю. Обратимся теперь к характеристикам рассеяния дискретной случайной величины.

Если х — случайная величина, а 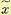 — среднее значение этой величины, то величина
— среднее значение этой величины, то величина  есть отклонение случайной величины от ее среднего значения. Это отклонение является случайной величиной, как и сама величина х.
есть отклонение случайной величины от ее среднего значения. Это отклонение является случайной величиной, как и сама величина х.
Средним отклонением ∆ называется среднее значение (математическое ожидание) абсолютной величины отклонения, т.е.
 (11.8)
(11.8)
Заметим, что без знака абсолютного значения было бы
Для рассмотренного выше примера бросания игральной кости
Среднее отклонение случайной величины является уже не случайной величиной, а обычным числом.
Дисперсией называется средний квадрат отклонения случайной величины от ее среднего значения. Она совпадает с центральным моментом второго порядка.
 (11.9)
(11.9)
Дисперсия может быть легко вычислена на основании свойства среднего значения:
т. е. она равна разности среднего квадрата и квадрата среднего значения случайной
величины. Так как всегда выполняется неравенство  , то дисперсия может быть только положительным числом:
, то дисперсия может быть только положительным числом:  .
.
Корень квадратный из дисперсии называется среднеквадратичным отклонением случайной величины от среднего значения:
Для рассмотренного выше примера бросания игральной кости
Среднеквадратичное отклонение
Укажем простейшие свойства среднеквадратичных отклонений. 1. При сложении независимых случайных величин
дисперсии складываются:
 о
о
Поэтому среднеквадратичное отклонение суммы независимых случайных величин
Эта формула часто применяется в измерительной технике и в автоматике для вычисления среднеквадратичных ошибок. 2. Пусть имеется n случайных величин
с одинаковыми средними значениями ж и с одинаковыми законами распределения. Тогда их среднее арифметическое

тоже будет случайной величиной с тем же самым средним значением  , но
, но
среднеквадратичное отклонение его будет в  раз меньше, чем для каждой из составляющих (в случае независимых случайных величин):
раз меньше, чем для каждой из составляющих (в случае независимых случайных величин):
Например, если производится п измерений одной и той же физической величины, то их среднее арифметическое, хотя тоже является случайной величиной, но всегда надежнее (имеет меньшее среднеквадратичное отклонение), чем каждое измерение в отдельности. Здесь случайные ошибки измерения в известной мере компенсируются. Но надо помнить, что систематические ошибки приборов при этом остаются в полной мере в составе среднего арифметического и никакой массовостью измерений скомпенсированы быть не могут.
3. Для n случайных величин, независимых и имеющих одно и то же среднее значение 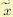 , среднее арифметическое будет при достаточно большом n как угодно мало отличаться от
, среднее арифметическое будет при достаточно большом n как угодно мало отличаться от
среднего значения  (с вероятностью, как угодно близкой к единице). Замечание в скобках означает, что это практически достоверно, но не абсолютно, потому что среднее арифметическое есть все же случайная величина. Таким образом, при большом n и указанных условиях
(с вероятностью, как угодно близкой к единице). Замечание в скобках означает, что это практически достоверно, но не абсолютно, потому что среднее арифметическое есть все же случайная величина. Таким образом, при большом n и указанных условиях
Этот закон больших чисел, доказанный П. Л. Чебышевым, имеет первостепенное значение для обработки экспериментальных данных и для учетной статистики.
Введем теперь понятие интегрального закона распределения. Интегральным законом распределения или функцией распределения называется вероятность того, что случайная величина примет значение, меньшее некоторого значения х. Математически эта формулировка записывается в виде
где ξ — текущее значение случайной величины х. Например, если график закона распределения дискретной случайной величины х имеет вид, показанный на рис. 11.5, а, то график функции распределения Р (х) для нее будет иметь вид, показанный на рис. 11.5, б. Он показывает, что вероятность того, что величина х получит значение меньше единицы, равна нулю; меньше трех—равна 0,2; меньше четырех — равна 0,6 и т. д. Функция распределения F (х) всегда возрастает с увеличением х, причем F (х) = 1 при наибольшем возможном значении жшах и остается равной единице при всех значениях х >xmах.
Например, для закона Пуассона (11.3), когда дискретная случайная 'величина может принимать значения х = 0, 1, 2, 3, . . ., функция распределения
 (11.10)
(11.10)

 (10.48)
(10.48) (10.49)
(10.49) , а T
, а T , Т
, Т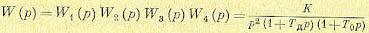 (10.51)
(10.51) — общий коэффициент усиления разомкнутой системы. Найдем характеристическое уравнение системы
— общий коэффициент усиления разомкнутой системы. Найдем характеристическое уравнение системы (10.52)
(10.52) (10.53)
(10.53)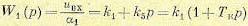 (10.54)
(10.54)