Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

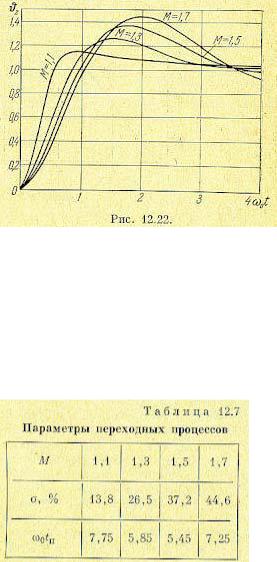
При повышенных требованиях по статической и динамической точности могут применяться л. а. х. типа О—1— 2—1— 2—3... (рис. 12.21), образованные из л. а. х. типа 2—1—2—3... (рис. 12.13) систем с астатизмом второго порядка.

Таким л. а. х. соответствует передаточная функция разомкнутой системы

(12.114)

Как и в случае систем с астатизмом первого порядка, здесь можно с достаточной степенью точности пользоваться универсальными формулами (12.86) — (12.89) и (12.95), (12.96).

Учет звеньев постоянного запаздывания и колебательных звеньев, а также введение границы малых постоянных времени может делаться анало.-гично изложенному выше.

Переходные процессы, соответствующие типовым л. а. х. Для л. а. х. типа 2—1—2 можно показать, что при заданной протяженности h асимптоты с единичным наклоном (рис. 12.13) выбор параметров, при котором обеспечивается минимальное значение показателя колебательности (12.83), вместе с тем соответствует некоторому оптимальному протеканию переходных процессов. При этом будет иметь место максимальное приближение кривой переходного процесса к некоторой экстремали, которая является экспонентной с постоянной

времени .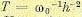

Чем больше протяженность участка h, тем меньше показатель колебательности и тем более благоприятным будет протекание переходного процесса, так как постоянная времени экспоненты будет меньше.

Определим вид переходного процесса при единичном входном воздействии 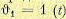для Случая использования л. а. х. типа 2—1—2 (рис. 12.13).;

Для нормированной передаточной функции (12.77)изображение Лапласа выходной величины будет иметь вид

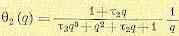(12.115)

Задаваясь различными значениями показателя колебательности, можно найти

относительные постоянные времени и затем построить переходный процесс для выходной величины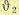 в функции безразмерного времени 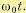. Переходные характеристики показаны на рис. 12.22. Параметры переходных процессов — перерегулирование

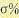и относительное время переходного процесса приведены в табл. 12.7.

Хотя эти кривые переходных процессов соответствуют л. а. х. типа 2—1—2 системы с астатизмом второго порядка (рис. 12.13), они с большой степенью точности могут использоваться для оценки переходных процессов при использовании л. а. х. других типов, изображенных, например, на рис. 12.16, 12.19 и 12.21, для которых характерным является наличие участка с наклоном —20 дб/дек в районе пересечения оси частот.

Различие будет наблюдаться в начальной части, если высокочастотная часть л. а. х. отличается от высокочастотной части л. а. х. типа 2—1—2, и в конечной части, если будут отличаться их низкочастотные части.

Таким образом, в случае нужды оценка переходных процессов может делаться по универсальным кривым, приведенным на рис. 12.22, во всяком случае для средней части кривой переходного процесса, которая показывает степень склонности системы к колебаниям.

Втех случаях, когда л. а. х. не имеет специального участка с наклоном — 20 дб/дек при переходе оси частот (см., например, рис. 12.18 и 12.20), оценка переходных процессов может быть сделана следующим образом.

Вкачестве исходной примем л. а. х. типа 1—2 (рис. 12.18). Ей соответствует передаточная

функция (12.102). Вводя единичное ступенчатое воздействие 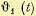можно аналогично изложенному выше построить нормированные переходные процессы в функции безразмерного

времени 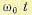(рис. 12.23). Здесь в качестве 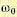принята частота пересечения асимптоты, имеющей наклон — 20 дб/дек, с осью частот (рис. 12.18).

Эти же кривые переходного процесса могут использоваться для оценки переходного процесса в случае использования л. а. х. другого типа, например 1—2—3 или 0—1—2 (рис. 12.20). Как и в предыдущем случае, различие может наблюдаться только в начальной и конечной стадиях переходного процесса.

Построение низкочастотной области желаемой л. а. х. Построение желаемой л. а. х. начинается с низкочастотной области. Из условий требуемой точности работы определяется положение контрольной точки или запретной области (см. рис. 12.11). Низкочастотная часть л. а. х. должна проходить не ниже контрольной точки или так, чтобы не заходить в запретную область.

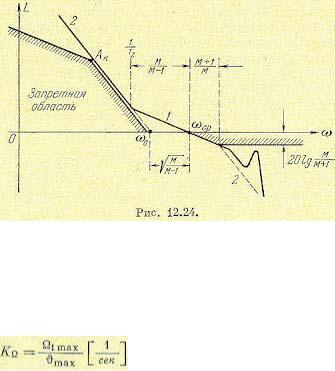
В следящих системах с астатизмом второго порядка положение первой низкочастотной асимптоты, имеющей наклон 40 дб/дек, определяется совершенно однозначно. Из условий облегчения задачи демпфирования выгодно сдвигать эту асимптоту как можно более влево, т. е. в сторону низких частот. Очевидно, что предельное положение первой асимптоты будет в том случае, когда она или пройдет через контрольную точку Ак, или сольется с правой границей запретной области (рис. 12.24).

Необходимое значение базовой частоты л. а. х. 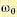и необходимый коэффициент усиления по разомкнутой цепи следящей системы определяются из выражения (12.63):

В следящих системах с астатизмом первого порядка необходимо определить положение двух первых асимптот, что можно сделать различным образом в зависимости от выбранного

значения первой сопрягающей частоты .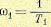

Если принять, что первая сопрягающая частота больше контрольной частоты сок не менее чем в 2—3 раза, то первые две асимптоты можно расположить так, чтобы через контрольную точку Ак прошла первая асимптота (рис. 12.25, а).

При этом коэффициент усиления по разомкнутой цепи или добротность по скорости 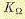будет иметь минимальную возможную величину, равную предельному значению, определяемому из (12.62):

что является благоприятным. Однако частота точки пересечения второй асимптоты с осью нуля децибел 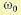будет значительно больше минимального достижимого значения, определяемого по требуемому предельному коэффициенту усиления по ускорению (12.63). Это является нежелательным, так как вся л. а. х. будет сдвигаться в область более высоких частот, что затрудняет демпфирование вследствие относительного возрастания влияния всех постоянных времени системы.

Если теперь принять, что первая сопрягающая частота 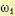меньше контрольной частоты по крайней мере в 2—3 раза, то первые две асимптоты можно расположить так, чтобы через контрольную точку Ак прошла вторая асимптота (рис. 12.25, б). При этом частота пересечения второй асимптоты с осью нуля децибел 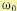будет иметь минимальную возможную величину, определяемую предельным значением добротности по ускорению (12.63), что является благоприятным с точки зрения облегчения демпфирования системы. Однако при этом требуемый общий коэффициент усиления по разомкнутой цепи будет в 2 — 3 раза превышать минимальное возможное значение, определяемое формулой (12.62). Увеличение общего коэффициента усиления может неблагоприятным образом сказаться на возрастании влияния помех и наводок на входе. Поэтому выбор того или иного расположения низкочастотной части л. а. х. относительно контрольной точки должен определяться конкретными условиями.

При отсутствии преобладания того или иного фактора оптимальным следует считать такое расположение низкочастотных асимптот (рис. 12.25, в), при котором первая сопрягающая частота о>1 совпадает с контрольной частотой сок.

Так как истинная л. а. х. в точке проходит ниже точки пересечения двух асимптот

на 3 дб, или на 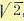, то вся л. а. х. при должна быть поднята вверх на 3 дб. При этом требуемое значение коэффициента усиления

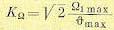(12.116)

Точке пересечения второй асимптоты с осью нуля децибел соответствует частота

(12.117)

В статических следящих системах, а также в системах стабилизации построение низкочастотной части делается в соответствии с формулами (12.69)-(12.74).

Построение средне- и высокочастотной частей л. а. х. В системах с аста-тизмом второго порядка (рис. 12.24) необходимо осуществить типовой переход оси нуля децибел в соответствии с рис. 12.13. При этом известно значение базовой частоты .

Требуемое значение постоянной времени Т2 определяется формулой (12.86). Среднечастотной части л. а. х. соответствует асимптота с единичным наклоном,

проходящая в интервале амплитуд

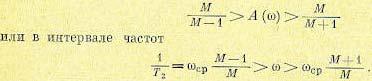(12.118)

Часть л. а. х., лежащая правее частоты среза, может иметь, вообще говоря, произвольный вид, определяемый имеющимися в системе звеньями. Однако в соответствии с изложенным выше необходимо выполнение следующих условий.

1. Высокочастотная часть л. а. х. не должна заходить в запретную область, образованную асимптотой с единичным наклоном, пересекающей ось нуля децибел в точке , и горизонтальной прямой, соответствующей

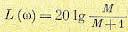(12.119)

2. Сумма постоянных времени и коэффициентов при .операторе в первой степени передаточных функций колебательных звеньев не должна превышать значения (12.95):

При построении желаемой л. а. х. в высокочастотной области вначале можно ориентироваться на наиболее простой ее вид и сформулировать ее при помощи одной асимптоты с наклоном 40 дб/дек, положение которой определяется постоянной времени

Эта л.а.х. показана в высокочастотной части на рис. 12.24 пунктирной линией. Она соответствует типу 2—1—2. При дальнейшем расчете вид высокочастотной части л. а. х. может уточняться. Однако два сформулированных выше условия не должны нарушаться. В окончательном виде высокочастотная часть л. а. х. может иметь произвольный вид, например показанный сплошной линией на рис. 12.24.

В следящих системах с астатизмом первого порядка необходимо вначале проверить возможность сведения желаемой л. а. х. к типу 1—2 или ее модификациям 1—2—3... Для этого необходимо исследовать возможность доведения суммы всех постоянных времени до значения, определяемого формулой (12.105):

При отрицательном ответе необходимо сформировать переход оси нуля децибел асимптотой с единичным наклоном так, как показано на рис. 12.25. Весь расчет ведется аналогично изложенному в.ыше для следящих систем с астатизмом второго порядка.

Исходные данные для расчета — базовая частота 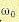и постоянная времени Т1 — известны по построению низкочастотной части л. а. х. (см. рис. 12.25).

Для статических систем расчет ведется аналогично расчету систем с астатизмом первого порядка. Вначале необходимо проверить возможность использования л. а. х. типа 0—1—2 (рис. 12.20) или ее модификации 0—1—2—3... по формуле (12.113). При отрицательном ответенеобходимо сформировать переход оси нуля децибел аналогично рис. 12.24 и 12.25.

Расчет корректирующих (демпфирующих) средств. По наиболее простой схеме расчета следящих систем корректирующие средства определяются сравнением желаемой передаточной

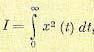
функции с передаточной функцией системы без корректирующих средств или сравнением л. а. х., соответствующих этим передаточным функциям.

Часто эта схема расчета оказывается слишком упрощенной, что затрудняет ее использование. Это объясняется главным образом трудностью непосредственного перехода в сложных случаях от имеющейся передаточной функции к желаемой, а также тем обстоятельством, что формирование высокочастотной части л. а. х. может быть выполнено многозначно. Бели вид желаемой л. а. х. в низкочастотной части является вполне определенным, то для ее высокочастотной части могут быть сформулированы лишь общие требования в отношении допустимой суммы постоянных времени и отсутствия пиков, заходящих в запретную зону (см. рис. 12.24).

Поэтому более гибкой оказываестя схема расчета, при которой построение желаемой л. а. х. и расчет корректирующих средств, обеспечивающих получение желаемой л. а. х., делаются в два этапа.

На первом этапе расчета на основании требований к точности строится желаемая л. а. х. и рассчитываются корректирующие средства, формирующие ее в низкочастотной части. При этом будет получена некоторая промежуточная система, имеющая требуемую точность, но не имеющая, возможно, требуемого запаса устойчивости.

В некоторых случаях возможно сформирование одновременно с низкочастотной частью л. а. х. ее средне-, а в простейших случаях и высокочастотной частей.

На втором этапе расчета уточняется вид и рассчитываются параметры корректирующих средств, формирующих средне- и высокочастотную части л. а. х. В результате должна быть получена система, обеспечивающая не только требуемую точность в типовых режимах, но и имеющая необходимый запас устойчивости.

§ 12.7. Об оптимальном синтезе

Под оптимальной системой автоматического регулирования или управления понимается система, которой тем или иным способом приданы наилучшие качества в каком-нибудь определенном смысле. Например, система может быть спроектирована так, чтобы она имела максимальную точность выполнения возложенной на нее задачи регулирования заданного объекта. Другим примером оптимизации является существование наиболее быстрого перехода системы из одного заданного состояния в другое или вообще из любого начального состояния в требуемое заданное при заданной ограниченной управляющей силе или мощности. Третьим примером оптимизации системы является обеспечение минимума затраты энергии на выполнение задачи управления при заданных внешних условиях. Четвертым примером может быть получение максимальной надежности работы аппаратуры системы при заданном ее весе. Пятым — достижение минимальной стоимости системы при заданном качестве выполнения ею определенной задачи управления и т. д.

Важно отметить четыре общих обстоятельства для любой оптимизации систем управления и регулирования.

При оптимизации системы в каждом отдельном случае должен быть правильно выбран критерий оптимальности, выраженный в той или иной математической форме. Например, при достижении максимальной точности системы критерием оптимальности может служить минимум ошибки регулирования, выраженный в виде интеграла

где х (t) — отклонение регулируемой величины от требуемого значения. Величина I называется функционалом, так как она зависит от выбора функции х (t) или, вернее, от неизвестного пока вида этой функции, который определится после расчета системы по минимуму функционала I. Критерием максимальной точности может являться также минимум статической ошибки при максимальном внешнем воздействии или минимум среднеквадратичной ошибки при случайном воздействии. В других случаях критерием будет минимум расхода энергии на выполнение управляемого процесса, максимум математического выражения какого-либо из

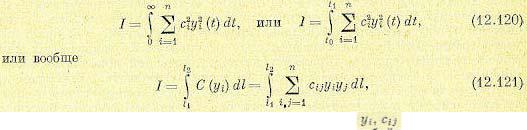
показателей надежности и т. п. При этом всегда функционал конструируется таким образом, чтобы оптимальности системы соответствовал именно минимум его (а не максимум) как в случае минимума, так и в случае максимума требуемого показателя. качества системы. Это всегда можно сделать. Чаще всего критерий оптимальности задается в виде интегрального квадратичного функционала от нескольких функций:

где С — некоторая квадратичная форма от величин — весовые коэффициенты, l может быть не только временем, но и любой другой физической или даже условной

комбинированной независимой переменной, а может быть как любой физической величиной, так и любой количественной оценкой того или иного свойства создаваемой системы. Однако математическое выражение критериев оптимальности может иметь не только форму (12.121), но и любую другую форму.

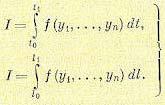(12.122)

Функционал, минимум которого нужно получить, в общем случае-может представлять любую желаемую комбинацию оценок различных качеств задаваемой системы. Заметим, что оптимальность системы по быстродействию является простейшим частным случаем для синтеза оптимальных систем, так как в этом случае в функционале (12.122) , причем I= t1 — t0 (время перехода системы из начального состояния в новое, заданное при t = t1).

Чаще всего в качестве подынтегральных функций в (12.122) используются положительно определенные квадратичные формы от фазовых координат , управляющих величин 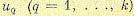, например, в виде

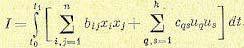(12.123),

Введя понятия критерия оптимальности, т. е., по сути дела, критерия качества системы, можно попытаться сформулировать задачу оптимального управления.

Пусть 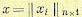— матрица-столбец фазовых координат, а 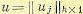— матрицастолбец управляющих воздействий, которые принадлежат некоторому множеству 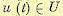и считаются допустимыми. Из множества допустимых управлений требуется выбрать такое,

которое переводит управляемый объект из начального положения 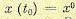в конечное 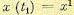и минимизирует принятый функционал качества. Это управление и соответствующая ему траектория называются оптимальными. Однако эта формулировка является лишь возможной, распространенной, но не единственной (см., например, § 11.9).

В условии задачи оптимизации любого одного из качеств системы фигурируют некоторые ограничения других ее свойств в виде заданной управляю щейсилы или мощности, заданного веса, заданных интервалов возможного изменения параметров регулятора и объекта и т. п. При достижении максимальной точности может быть задано ограничение стоимости, веса, внешних возмущений. При достижении максимальной надежности системы может быть, кроме указанных ограничений, задано ограничение ошибок системы, или пределы допустимого отклонения параметров реальных элементов системы от их номинальных (запроектированных) значений. Для практики учет ограничений при оптимизации системы чрезвычайно важен, так как всякая реальная система характеризуется ограниченной мощностью, инерционностью и всегда целым комплексом качеств (точность, устойчивость, быстродействие, надежность, стоимость, вес,

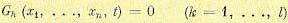
простота эксплуатации и соответствие своему практическому назначению по целому ряду конкретных физико-химических свойств), которые надо соблюсти в определенных пределах при оптимизации одного, наиболее важного из них. Оптимизироваться может также не одно качестйо, а определенная комбинация качеств.

Рассмотрим основные виды ограничений.

1. Ограничения на фазовые координаты и управления

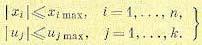(12.124)

При отсутствии ограничений подобного рода говорят, что задача оптимизации относится к числу вариационных задач в открытой области. Введение подобных ограничений приводит к задаче в закрытой области, что значительно усложняет решение и часто делает невозможным использование классических вариационных методов (см. главу 23).

2. Ограничения типа голономных связей^

где Gk — некоторые функции, которые в общем случае могут зависеть от времени. 3. Ограничения типа неголономных связей в виде дифференциальных уравнений

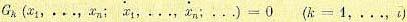(12.126) 4. Изопериметрические ограничения в виде функционалов

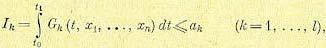(12.127)

где в правой части находятся некоторые постоянные числа, которые не должны превосходиться. В качества аk могут фигурировать такие величины, как, например, предельная температура нагревания, количество выделившегося тепла, расход энергии или рабочего тела и т.п.

Отличие синтеза оптимальной системы от синтеза системы по заданным показателям качества, рассмотренного ранее, состоит в том, чтобы добиться не просто требуемых показателей, а наилучших показателей, т. е. «выжать» из системы все, что она может дать неопределенному виду качества, наиболее важному для этой системы, при соблюдении Заданных требований до всем необходимым другим ее свойствам. Поэтому задача оптимизации систем является в существе своем задачей вариационного типа, когда требуется подобрать программу и закон регулирования, а также и параметры системы управления (регулятора) таким образом, чтобы получить минимум функционала, который в данном случае служит критерием оптимальности системы.

При оптимизации систем управления и регулирования необходимо различать два класса задач, решаемых последовательно: оптимизацию программы регулирования (или управления) и оптимизацию закона регулирования .(или управления). Первый из этих классов задач возникает не всегда, а лишь , тогда, когда процессы в управляемой системе (например, движение управляемого объекта, ход физического или химического процесса) задаются определенной программой изменения регулируемой величины во времени или же когда выбирается определенная связь между переменными (координатами или другими физическими величинами), которая должна соблюдаться независимо от момента времени, другими словами, когда имеется

.либо временная, либо параметрическая программа управления.

Примером временной программы управления может служить программа изменения угла тангажа во времени при подъеме или спуске летательного аппарата. Примером параметрической программы управления могут служить методы автоматического наведения или самонаведения, например, по принципу параллельного сближения и др.

Вслучае оптимизации той или иной программы управления она не задается, а отыскивается

врезультате расчета по какому-либо критерию оптимальности, например по минимуму затраты энергии при желаемом маневре летательного аппарата в процессе его движения или при сближении двух аппаратов в процессе наведения.

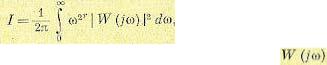
Вторым самостоятельным классом задач, как указывалось, является оптимизация закона регулирования, т. е. наилучшее построение регулятора (системы управления) для осуществления заданной программы управления. Эта задача может иметь место во всех автоматических системах независимо от того, оптимизировалась ли программа управления или она была иначе задана, в том числе и в случае простого поддержания постоянного значения регулируемой величины и в случае любой обычной следящей системы. При оптимизации закона регулирования, как и обычно, рассматриваются уравнения динамики системы в отклонениях от требуемых величин (от программы).

Внастоящее время одной из основных проблем в оптимальном синтезе стала проблема весовых коэффициентов в функционалах качества типа (12.121) или (12.123). Это связано с тем, что попытка введения более или менее сложного функционала качества, учитывающего весь комплекс требований к системе регулирования (точность, расход энергии, надежность, вес, технологичность и т. п.), неизбежно приводит к необходимости сопоставить между собой отдельные требования, что и должно делаться посредством весовых коэффициентов. Однако назначение этих коэффициентов лока осуществляется произвольно и, в лучшем случае, по некоторым экспертным оценкам, что иногда дает им субъективный характер.

Всвязи с необходимостью удовлетворения в процессе синтеза многим различным требованиям возникла трактовка оптимального синтеза как такого построения системы регулирования или управления, при котором все необходимые требования могут быть выполнены простейшим образом [10]. В качестве критерия простоты вводится, например, функционал в частотной «области

В статических системах (r = 0) значение (12.128) совпадает с эквивалентной полосой пропускания разомкнутой системы, что разъясняет физическую сущность введенного функционала. Чем меньше требуется полоса пропускания при выполнении всех качественных требований (точность, запас устойчивости, быстродействие и т. п.), тем проще реализация этой системы. В [10] показано, в частности, что приведенный в § 12.6 метод синтеза эвристическим путем приводит к минимизации функционала (12.128). Подобный метод синтеза может быть назван оптимальным синтезом по заданным, качественным показателям.

Существуют различные способы оптимизации или, иначе говоря, методы синтеза оптимальных систем, как аналитические, так и машинные. В основе этих способов лежат математические вариационные методы. Каждый из них сопровождается различными вариантами приемов доведения решения задачи до конца в числовом виде. Оказывается, что это последнее представляет во многих случаях особенно трудную задачу даже при наличии решения в принципиальном виде. Поэтому чаще всего (во всяком случае для систем высокого порядка) приходится применять вычислительные машины с использованием таких вычислительных методов, как метод градиента, метод наискорейшего спуска, и других специально разрабатываемых приемов. Для некоторых простейших задач имеются аналитические решения, иногда с привлечением изображений на фазовой плоскости. Заметим, что ранее (см. § 11.9) уже был рассмотрен метод синтеза линейной оптимальной системы при случайных воздействиях по минимуму среднеквадратичной ошибки (задача Винера). Поэтому в дальнейшем изложении эта задача уже фигурировать не будет.

Оптимальные законы регулирования при учете реально имеющихся ограничений часто получаются нелинейными (см. главу 23).

§ 12.8. Использование классических вариационных методов Пусть в качестве критерия качества рассматривается функционал вида

=

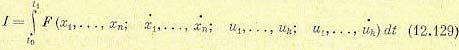при заданных граничных условиях 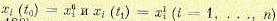. В подынтегральное выражение (12.129) здесь не входят производные выше первой от координат и управлений 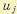. Если не наложено никаких ограничений, то 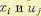принадлежат открытым областям.

Решение задачи в этом случае дается уравнениями Эйлера, записанными для всех координат и всех управлений, входящих в (12.129):

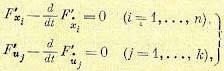(12.130)

где F' — частные производные от подынтегральной функции (12.129) по соответствующим

переменным. Это решение определяет пучок интегральных кривых (экстремалей) 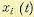, из которых необходимо выбрать траекторию, проходящую через заданные начальную и конечную точки.

При этом функции 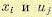должны принадлежать к так называемому классу функций 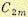, т. е. должны иметь 2m непрерывных производных. В рассматриваемом случае (12.129)

наивысшая производная является первой 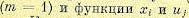, должны иметь две непрерывные производные.

Кроме того, для установления факта минимизации функционала (12.129) необходимо

удостовериться, что вдоль экстремалей выполняются условия 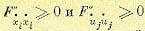. Эти условия аналогичны требованию положительности второй производной в точке минимума функции

.

Однако задача без ограничений не имеет смысла применительно к системам регулирования и управления. Введем ограничения в виде связей типа (12.125) или (12.126). Тогда в уравнениях (12.130) вместо функции Р должна использоваться функция

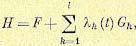(12.131)

где — произвольные множители Лагранжа, в общем случае зависящие от времени t. Это будет вариационная задача на так называемый условный экстремум (т. е. при наличии наложенных связей).

При учете связей в виде дифференциальных уравнений класс функций С2m должен определяться по наивысшей производной выражения (12.131).

Если рассматривается одна переменная х (t), но функционал включает в себя производные х(t) более высоких порядков и имеет, например, вид

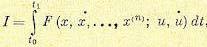(12.132)

то уравнения Эйлера будут иметь вид

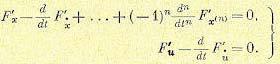(12.133)

Как и ранее, при наличии связей вместо функции F должна рассматриваться функция H, определяемая (12.131). Класс функций С2m определяется по наивысшей производной (12.131) m- го порядка.

Отметим, что решение уравнений (12.130) или (12.133) часто приводит к корням характеристического уравнения, половина которых лежит в левой, а половина — в правой

полуплоскости. Это наблюдается при использовании квадратичных функционалов и конечном

времени регулирования .

Для устранения неустойчивости, которая получится в случае присоединения подобного регулятора к системе (если, конечно, не обеспечивается его отключение после завершения требуемого процесса перевода из одного состояния в другое), можно, например, действовать аналогично изложенному в § 11.9 и отбросить в решении те полюсы передаточной функции, которые лежат в правой полуплоскости. Это соответствует, вообще говоря, переходу к функционалу вида

т. е. бесконечному времени регулирования.

В этом случае искомые функции должны принадлежать к классу Ст, причем производная т- го порядка может иметь разрыв первого рода в точке t = 0.

При использовании изопериметрических ограничений типа (12.127) задача оптимизации решается также в соответствии с уравнениями (12.131), но должна быть использована функция

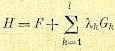(12.135)

где 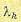— произвольные постоянные множители Лагранжа. В этом случае для определения

произвольных постоянных и множителей 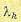к граничным условиям должна добавляться совокупность условий (12.127).

Рассмотрим простейшие примеры. Пусть объект управления описывается уравнением

Цель управления заключается в переводе объекта из состояния у = 0 при t = О в состояние у=у0 при t=Т. В качестве критерия качества примем минимум функционала

(12.137)

где 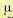— некоторый весовой коэффициент. Для функции (12.131)

Совместное решение (12.136) и (12.139) дает характеристическое уравнение

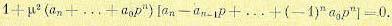(12.140)

Это уравнение содержит только четные степени р. Поэтому, если половина корней лежит в левой полуплоскости, то половина — в правой.

Упростим задачу и положим 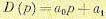. Тогда получим характеристическое уравнение в виде

Решение его дает корни