
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf
2. Моменты времени относятся к разным интервалам. Тогда среднее значение произведения скоростей будет равно нулю:
так как произведения с положительным и отрицательным знаками будут равновероятными. Корреляционная функция будет равна
где Р1 — вероятность нахождения моментов времени 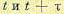 в одном интервале, а
в одном интервале, а  — вероятность нахождения их в разных интервалах. Вероятность появления перемены скорости на малом промежутке времени
— вероятность нахождения их в разных интервалах. Вероятность появления перемены скорости на малом промежутке времени 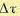 пропорциональна этому промежутку и
пропорциональна этому промежутку и
равна  . Вероятность отсутствия перемены скорости для этого же промежутка будет
. Вероятность отсутствия перемены скорости для этого же промежутка будет
 .
.
Для интервала времени т вероятность отсутствия перемены скорости, т. е. вероятность нахождения моментов времени  в одном интервале постоянной скорости, будет равна произведению вероятностей отсутствий перемены скорости на каждом элементарном промежутке
в одном интервале постоянной скорости, будет равна произведению вероятностей отсутствий перемены скорости на каждом элементарном промежутке 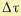 , так как.эти события независимые.
, так как.эти события независимые.
В результате для конечного промежутка 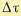 получаем
получаем
Устремив —> 0 и переходя к пределу, получим
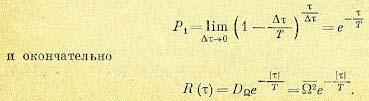 (11.80)
(11.80)
Знак модуля при  поставлен вследствие того, что выражение (11.80) должно соответствовать четной функции. Выражение для корреляционной функции совпадает с (11.79). Поэтому спектральная плотность рассматриваемого процесса должна совпадать с (11.78):
поставлен вследствие того, что выражение (11.80) должно соответствовать четной функции. Выражение для корреляционной функции совпадает с (11.79). Поэтому спектральная плотность рассматриваемого процесса должна совпадать с (11.78):
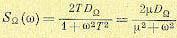 (11.81)
(11.81)
Заметим, что в отличие от (11.78) формула спектральной плотности (11.81) записана для угловой скорости процесса (рис. 11.22). Если перейти от угловой скорости к углу, то получится нестационарный случайный процесс с дисперсией, стремящейся к бесконечности. Однако в большинстве случаев следящая система, на входе которой действует этот процесс, обладает астатизмом первого и более высоких порядков. Поэтому первый коэффициент ошибки с0 у следящей системы равен нулю и ее ошибка будет определяться только входной скоростью и производными более высоких порядков, относительно которых процесс стационаре. Это дает возможность использовать спектральную плотность (11.81) при расчете динамической ошибки следящей системы.
3. Н е р е г у ля р н а я к а чк а. Некоторые объекты, например корабли, самолеты и другие, находясь под действием нерегулярных возмущений
(нерегулярное волнение, атмосферные возмущения и т. п.), движутся по случайному закону. Так

где  — некоторая известная неслучайная функция времени (синусоида, экспонента, степенная функция и т. п.).
— некоторая известная неслучайная функция времени (синусоида, экспонента, степенная функция и т. п.).
Если математическое ожидание величины х равно нулю, то и математическое ожидание случайной функции  . Корреляционная функция в этом случае
. Корреляционная функция в этом случае
 (11.87)
(11.87)
где дисперсия  .
.
Рассмотрим случайную функцию х (t), которая может быть представлена в виде суммы математического ожидания 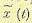 и элементарных случайных функций:
и элементарных случайных функций:
 (11.88)
(11.88)
Здесь  — случайные взаимно некоррелированные коэффициенты с нулевым математическим ожиданием.
— случайные взаимно некоррелированные коэффициенты с нулевым математическим ожиданием.
Представление случайной функции в виде суммы ее математического ожидания и взаимно некоррелированных элементарных случайных функций называется каноническим разложением. Случайные коэффициенты носят название коэффициентов канонического разложения, а функции
 — координатных функций.
— координатных функций.
При использовании канонического разложения значительно упрощается выполнение различных операций над случайными функциями (дифференцирование, интегрирование, решение линейных дифференциальных уравнений и т. п.). Так, например, производная от (11.88) будет
 (11.89)
(11.89)
Аналогичным образом интегрирование (11.88) дает х (I) <И = (х (г) сИ+^У^ Г XV (I) 6,
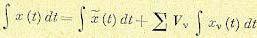 (11.90)
(11.90)
Для нахождения, канонического разложения случайных функций существуют различные методы [108].
Из (11.88) может быть найдена корреляционная функция
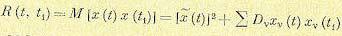 (11.91)
(11.91)
Здесь  — дисперсии коэффициентов канонического разложения. Таким образом, корреляционная функция может быть выражена через те же координатные функции. Для стационарной случайной функции, заданной в интервале — Т < t < Т, разность
— дисперсии коэффициентов канонического разложения. Таким образом, корреляционная функция может быть выражена через те же координатные функции. Для стационарной случайной функции, заданной в интервале — Т < t < Т, разность 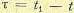 изменяется в интервале — 2Т <
изменяется в интервале — 2Т <  < 2 Т и разложение корреляционной функции
< 2 Т и разложение корреляционной функции
может быть задано в виде ряда Фурье:
 (11.92)
(11.92)
где 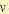 — целые числа.
— целые числа.
Этому выражению соответствует каноническое разложение самой случайной функции
(11.93)
где  — взаимно некоррелированные случайные величины с нулевыми
— взаимно некоррелированные случайные величины с нулевыми
математическими ожиданиями и с одинаковыми дисперсиями 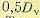 В разложении (11.92) должны отсутствовать нечетные гармоники. Тогда ряд (11.93) будет содержать только четные гармоники, что соответствует периоду 2 Т (интервалу — Т < t < Т).
В разложении (11.92) должны отсутствовать нечетные гармоники. Тогда ряд (11.93) будет содержать только четные гармоники, что соответствует периоду 2 Т (интервалу — Т < t < Т).
Если разность между двумя соседними гармониками  устремить к нулю, что соответствует
устремить к нулю, что соответствует  можно представить в виде
можно представить в виде

 (11.94)
(11.94)
Здесь введена спектральная плотность стационарного процесса (см. § 11.5)
являющаяся изображением Фурье корреляционной функции  .
.
§ 11.7. Прохождение случайного сигнала через линейную систему
Рассмотрим линейную систему (рис. 11.25) с передаточной функцией W(р) и функцией веса  . Пусть на входе действует случайный сигнал
. Пусть на входе действует случайный сигнал  с корреляционной функцией
с корреляционной функцией
 .
.
Выходной сигнал х2 (t) на основании формулы свертки (7.44)
Рассматривая в этой формуле математические ожидания, имеем
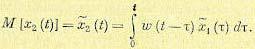 (11.95)
(11.95)
Для получения корреляционной функции на выходе запишем исходную формулу для центрированных значений 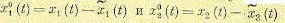 для двух моментов времени:
для двух моментов времени:
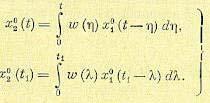 (11.96)
(11.96)
После перемножения получим
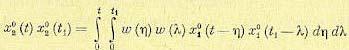 (11.97)
(11.97)
Далее, переходя к математическому ожиданию, можно найти корреляционную функцию
 (11.98)
(11.98)
Для определения дисперсии на выходе О2(1) в формуле (11.98) следует положить . Тогда
. Тогда
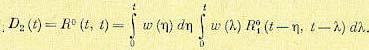 (11.99)
(11.99)
В случае использования канонического разложения случайной функции
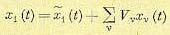 (11.100)
(11.100)
выходная величина может быть представлена в виде
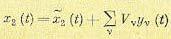 (11.101)
(11.101)


В линейной системе изображения Фурье 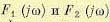 связаны между собой посредством частотной передаточной функции:
связаны между собой посредством частотной передаточной функции:
Отсюда можно найти
 (11.109)
(11.109)
Таким образом, спектральная плотность выходной величины может быть получена умножением спектральной плотности входной величины на квадрат модуля частотной передаточной функции линейной системы. Отметим, что приведенное выше доказательство, вообще говоря, не является строгим, так как существование стационарного случайного процесса на выходе не доказано.
При известной спектральной, плотности  выходной величины может быть найдена корреляционная функция
выходной величины может быть найдена корреляционная функция  по преобразованию Фурье (11.66) или (11.68).
по преобразованию Фурье (11.66) или (11.68).
Получим выражение (11.109) более строго. Для этого используем формулу (11.107). Так как в реальных системах весовая функция тождественно равна нулю при t < 0, то нижние пределы интегрирования можно положить равными  . Полагая, что на входе действует
. Полагая, что на входе действует
центрированный процесс 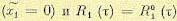 , имеем
, имеем
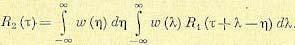 (11.110)
(11.110)
Найдем теперь спектральную плотность для выходного сигнала. Она связана с корреляционной функцией соотношением (11.65):
Подставляя в последнюю формулу значение корреляционной функции из (11.110), получаем
Последнее выражение совпадает с (11.109), что и требовалось доказать, Для нахождения дисперсии, или среднего квадрата выходной величины, необходимо
проинтегрировать по всем частотам спектральную плотность:
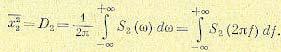 (11.112)
(11.112)
Отметим, что закон распределения для случайной величины может, вообще говоря, меняться при прохождении ее через линейную систему. Однако, в случае, если на входе линейной системы имеется нормальное распределение случайной величины х1 (t), то на выходе для случайной величины х2 (t) также будет иметь место нормальное распределение.
При вычислении интеграла (11.112) обычно приходится иметь дело с подынтегральным выражением вида

где |
представляют собой некоторые полиномы от комплексной переменной . |
|
Наивысшую степень знаменателя обозначим 2n. Наивысшая степень числителя в реальной |
системе может быть не выше 2n — 2. Для удобства интегрирования написанное выше выражение обычно представляют в виде
Полином 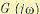 содержит только четные степени
содержит только четные степени 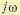 . Полином
. Полином 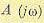 для устойчивой системы может иметь корни только в верхней полуплоскости. Область устойчивости оказалась в верхней полуплоскости вследствие того, что была использована подстановка
для устойчивой системы может иметь корни только в верхней полуплоскости. Область устойчивости оказалась в верхней полуплоскости вследствие того, что была использована подстановка  , а
, а
множитель j означает поворот комплексного числа на угол 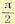 .
.
Таким образом, вычисление дисперсии (11.112) можно свести к нахождению интеграла
 (11.113)
(11.113)
В общем случае, при любом га для устойчивой системы интеграл 1п может быть представлен в виде [38]
 (11.114)
(11.114)
где
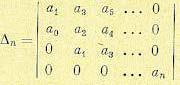 (11.115)
(11.115)
совпадает со старшим определителем Гурвица, а числитель определяется выражением
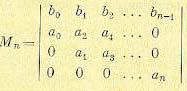 (11.116)
(11.116)
Интегралы такого вида вычислены до n = 7 и сведены в таблицы (см. приложение 2). Заметим, что знаменатель правых частей приведенных в приложении 2 формул
представляет собой  — определитель Гурвица. На границе колебательной устойчивости этот определитель обращается в нуль, а дисперсия выходной величины будет стремиться к бесконечности.
— определитель Гурвица. На границе колебательной устойчивости этот определитель обращается в нуль, а дисперсия выходной величины будет стремиться к бесконечности.
В заключение рассмотрим два важных случая прохождения случайного сигнала через линейную систему.
Статистическое дифференцирование. При поступлении случайного сигнала на идеальнбе дифференцирующее устройство с передаточной функцией W (р) = р спектральная плотность выходной величины (производной от входной величины) может быть получена умножением спектральной плотности входной величины на  :
:
 (11.117)
(11.117)
при двойном дифференцировании — на 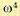 и т. д.
и т. д.

Статистическое интегрирование. При поступлении случайного сигнала на идеальное
интегрирующее звено с передаточной функцией спектральная плотность выходной величины (интеграла
спектральная плотность выходной величины (интеграла
от входной величины) может быть получена делением интегральной плотности входной величины на  :
:
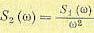 (11.118)
(11.118)
при двойном интегрировании — на 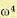 и т. д.
и т. д.
§ 11.8. Расчет установившихся ошибок в автоматических системах
Замкнутая система автоматического регулирования может находиться под воздействием случайного задающего сигнала g (t) и случайной помехи f (t), приложенной в произвольной точке системы (рис. 11.26).
Корреляционные функции и спектральные плотности задающего воздействия и помехи будем считать известными. Конечной целью расчета является нахождение корреляционных функций и спектральных плотностей выходной величины у (t) и ошибки х (t). Обычно ограничиваются более узкой задачей и определяют только среднеквадратичную ошибку системы регулирования. Это может быть сделано посредством интегрирования по всем частотам спектральной плотности ошибки или через корреляционную функцию ошибки х (t).
В простейшем случае, когда управляющее воздействие g (t) представляет собой, случайный
стационарный процесс со спектральной плотностью  , а помеха отсутствует; f(t) = 0, расчет жожно свести к рассмотренной выше схеме (рис. 11.25). Тогда спектральная плотность ошибки
, а помеха отсутствует; f(t) = 0, расчет жожно свести к рассмотренной выше схеме (рис. 11.25). Тогда спектральная плотность ошибки
будет (11.119)
(11.119)
Частотная передаточная функция по ошибке 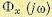 связана с частотными передаточными функциями разомкнутой
связана с частотными передаточными функциями разомкнутой 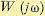 и замкнутой
и замкнутой 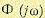 системы соотношением
системы соотношением
Таким образом, для спектральной плотности ошибки получаем
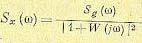 (11.120)
(11.120)
Интегрирование этого выражения по всем частотам позволяет определить дисперсию и среднеквадратичное значение ошибки:
 (11.121)
(11.121)
Вычисление дисперсии и среднеквадратичной ошибки через корреляционные функции может производиться на основании формулы (11.107). В качестве функции веса в
рассматриваемом случае должна использоваться функция веса для ошибки  , связанная с частотной передаточной функцией по ошибке преобразованием Фурье
, связанная с частотной передаточной функцией по ошибке преобразованием Фурье

После нахождения корреляционной функции ошибки 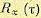 дисперсия определяется
дисперсия определяется
подстановкой 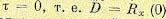 .
.
Однако нахождение среднеквадратичной ошибки посредством использования спектральных плотностей оказывается обычно более простым и поэтому применяется чаще.
В другом простейшем случае, когда задающее воздействие 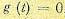 , а помеха
, а помеха
представляет собой случайный стационарный процесс со спектральной плотностью 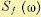 , аналогичным образом можно найти спектральную плотность ошибки:
, аналогичным образом можно найти спектральную плотность ошибки:
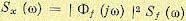 (11.122)
(11.122)
В этом выражении 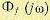 представляет собой частотную передаточную функцию;
представляет собой частотную передаточную функцию;
связывающую изображения Фурье ошибки х (t) и помехи f (t).
В частном случае, когда помеха f (t) действует на входе системы в месте приложения задающего воздействия, в формуле (11.101) должна использоваться частотная передаточная функция замкнутой системы
 (11.123)
(11.123)
Рассмотрим теперь общее выражение спектральной плотности ошибки для случая, когда задающее воздействие g (t) и помеха f (t) действуют одновременно (рис. 11.26).
Обозначим через 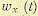 весовую функцию для ошибки по задающему воздействию и через
весовую функцию для ошибки по задающему воздействию и через 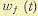 весовую функцию для ошибки по помехе. Тогда ошибку можно представить в виде
весовую функцию для ошибки по помехе. Тогда ошибку можно представить в виде
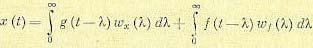 (11.124)
(11.124)
Подставим это выражение для ошибки в формулу корреляционной функции (11.51). В результате получим
где  — взаимные корреляционные функции.
— взаимные корреляционные функции.
Для нахождения спектральной плотности ошибки левую и правую части (11.125) умножим на  и проинтегрируем по
и проинтегрируем по 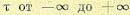 . В результате выкладок, аналогичных тем, которые были проделаны при выводе формулы (11.111), получим
. В результате выкладок, аналогичных тем, которые были проделаны при выводе формулы (11.111), получим
 (11.126)
(11.126)
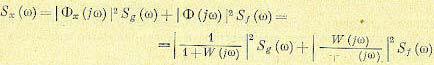
В этом выражении 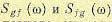 представляют собой взаимные спектральные плотности
представляют собой взаимные спектральные плотности
полезного сигнала и помехи, а  — частотные передаточные функции для ошибки по задающему воздействию и помехе. Звездочкой обозначен сопряженный комплекс. При отсутствии корреляции между полезным сигналом и помехой формула (11.126)
— частотные передаточные функции для ошибки по задающему воздействию и помехе. Звездочкой обозначен сопряженный комплекс. При отсутствии корреляции между полезным сигналом и помехой формула (11.126)
упрощается:
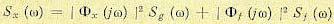 (11.127)
(11.127)
В частном случае, когда помеха действует на входе в месте приложения управляющего воздействия и корреляция между ними отсутствует, формула (11.127) может быть представлена в следующем виде:
(11.128)
так как для этого случая частотная передаточная функция  совпадает с частотной передаточной функцией замкнутой системы
совпадает с частотной передаточной функцией замкнутой системы 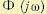 .
.
Все приведенные выше формулы для спектральной плотности ошибки х (t) могут быть легко переписаны для спектральной плотности выходной величины у (t), если в них заменить частотную передаточную функцию для ошибки  на частотную передаточную функцию
на частотную передаточную функцию
замкнутой системы 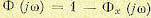 .
.
§ 11.9. Расчеты,по минимуму среднеквадратичной ошибки
Если на автоматическую систему действуют одновременно полезный сигнал и помеха, то возникает задача оптимального расчета системы с тем, чтобы получить наименьшую результирующую ошибку. С точки зрения наилучшего воспроизведения полезного сигнала система должна иметь возможно большую полосу пропускания, а с точки зрения наилучшего подавления помехи система, наоборот, должна иметь возможно меньшую полосу пропускания. Критерием получения оптимального решения здесь будет минимальное значение результирующей ошибки системы, определяемой полезным сигналом и помехой.
Для случайных величин наиболее просто определить среднеквадратичную ошибку, поэтому ее и используют для оценки точности автоматической системы.
Рассмотрим расчет системы по критерию минимума среднеквадратичной ошибки при одновременном действии полезного сигнала и помехи.
Согласно этому критерию нежелательность ошибки пропорциональна квадрату ее величины. Такая постановка является часто логичной, но она не может> конечно, претендовать на полную универсальность. В некоторых случаях, например при стрельбе по какой-либо цели, все ошибки, большие некоторого значения, являются одинаково нежелательными. Однако средний квадрат ошибки системы регулирования
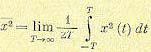 (11.129)
(11.129)
практически во всех случаях является наиболее просто вычисляемой величиной, что и определило использование этого критерия.
Возможны несколько формулировок задачи. Наиболее просто задача может быть сформулирована так. Если имеется какая-то система автоматического регулирования заданной структуры, то необходимо так выбрать параметры этой системы, чтобы получить минимум среднеквадратичной ошибки при заданных статистических характеристиках полезного сигнала и помехи.
Эта задача решается следующим образом. По спектральной плотности ошибки путем ее интегрирования находится дисперсия. Дисперсия получается зависящей от вероятностных характеристик полезного сигнала, помехи и параметров системы. Затем ищутся условия, которые должны быть наложены на параметры системы, чтобы получить минимум дисперсии. При

 (11.82)
(11.82) — резонансная частота,
— резонансная частота, 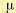 — параметр затухания, D — дисперсия. Значения
— параметр затухания, D — дисперсия. Значения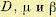 находятся обычно путем обработки экспериментальных данных (натурных испытаний). Корреляционной функции (11.82) соответствует спектральная плотность (см. табл. 11,3)
находятся обычно путем обработки экспериментальных данных (натурных испытаний). Корреляционной функции (11.82) соответствует спектральная плотность (см. табл. 11,3)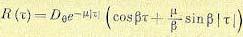 (11.84)
(11.84) (11.85)
(11.85)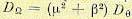 .
. (11.86)
(11.86) определяется формулой (11.95), а координатные функции
определяется формулой (11.95), а координатные функции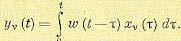 (11.102)
(11.102) (11.103)
(11.103)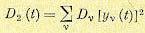 (11.104)
(11.104)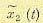 и координатных функций
и координатных функций  в соответствии с выражениями (11.95) и (11.102) могут использоваться различные методы построения переходных процессов (см. главу 7),
в соответствии с выражениями (11.95) и (11.102) могут использоваться различные методы построения переходных процессов (см. главу 7), зависит только от сдвига
зависит только от сдвига  . Однако на выходе линейной системы процесс некоторое время после включения будет устанавливаться и не будет стационарным. Корреляционная функция на выходе может быть получена из общего выражения (11.98);
. Однако на выходе линейной системы процесс некоторое время после включения будет устанавливаться и не будет стационарным. Корреляционная функция на выходе может быть получена из общего выражения (11.98);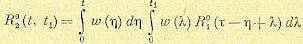 (11.105)
(11.105) стремятся к некоторым пределам, которые определяют стационарный процесс на выходе. Они могут быть найдены из
стремятся к некоторым пределам, которые определяют стационарный процесс на выходе. Они могут быть найдены из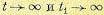 .
. и функцией веса
и функцией веса  действует белый шум с корреляционной функцией
действует белый шум с корреляционной функцией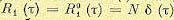 . Тогда в соответствии: с (11.106) дисперсия на выходе будет
. Тогда в соответствии: с (11.106) дисперсия на выходе будет , так как звено не является устойчивым, а оно находится на границе устойчивости (нейтральноустойчиво).
, так как звено не является устойчивым, а оно находится на границе устойчивости (нейтральноустойчиво).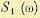 . Тогда можно легко найти спектральную плотность
. Тогда можно легко найти спектральную плотность  выходного сигнала. Действительно, по определению спектральная плотность на входе связана с изображением Фурье
выходного сигнала. Действительно, по определению спектральная плотность на входе связана с изображением Фурье  случайной величины
случайной величины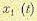 соотношением (11.61):
соотношением (11.61):