
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf
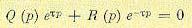
 (14.62)
(14.62)
Сравнивая (14.61) и (14.62), получаем искомое уравнение регулируемого объекта (трубопровода) без учета волновых процессов:
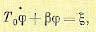 (14.63)
(14.63)
где
 (14.64)
(14.64)
Здесь То — прежняя постоянная объекта (14.30), а β — новый постоянный параметр
объекта, в выражении которого значение частной производной определяется для заданного объекта графически, аналогично рис. 14.8, или же расчетным путем.
К этому же уравнению объекта присоединяются прежние уравнения регулятора (14.47) — (14.51), где ϕ1 заменяется наϕ . Следовательно, в символической операторной форме уравнения данной системы регулирования давления без учета волновых явлений будут:
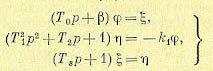 (14.65)
(14.65)
или
 (14.66)
(14.66)
Следовательно, в этом случае вместо дифференциального уравнения третьего порядка с запаздывающим аргументом (14.59) получается обыкновенное дифференциальное уравнение четвертого порядка.
§ 14.3. Исследование устойчивости и качества регулирования
В § 14.1 были приведены уравнения линейных систем с запаздыванием, которые для разомкнутой цепи имели вид
 (14.67)
(14.67)
а для замкнутой системы
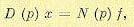 (14.68)
(14.68)
где
 (14.69)
(14.69)
В § 14.2 при выводе уравнений для одной линейной системы автоматического регулирования с распределенными параметрами было показано; что они сводятся к тому же самому виду во всех тех случаях, когда распределенное звено системы описывается волновым уравнением в частных производных типа (14.31) или (14.29). Характеристическое уравнение для таких систем с распределенными параметрами и систем с запаздыванием имеет согласно (14.69) трансцендентный вид
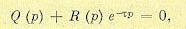 (14.70)
(14.70)
где Q(р) и P(р) — обыкновенные многочлены, причем степень R(р) обычно меньше или в крайнем случае равна степени Q (р).
Уравнение (14.70) записывается иногда и в другом виде, например:
или
Могут встретиться уравнения и более сложного вида:
и т. п.
Рассмотрим характеристическое уравнение вида (14.70). Известно, что решение дифференциально-разностных уравнений (14.68) можно записать в виде некоторых рядов и что для затухания этого решения, т. е. для устойчивости системы, необходимо и достаточно, чтобы все корни трансцендентного характеристического уравнения (14.70) имели отрицательные вещественные части. Но в отличие от обыкновенного
алгебраического уравнения здесь вследствие наличия множителя e−τp уравнение может иметь бесконечное количество корней.
К указанным системам применимы критерий устойчивости Михайлова и критерий устойчивости Найквиста в их прежних формулировках (см. главу 6). Однако здесь
вследствие наличия множителя e− jwt существенно изменяется очертание как кривой Михайлова замкнутой системы
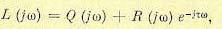 (14.71)
(14.71)
так и амплитудно-фазовой характеристики разомкнутой цепи, построенной по частотной передаточной функции
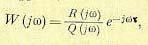 (14.72)
(14.72)
причем размыкание системы производится по определенному правилу, которое дается ниже.
Из кривой Михайлова не получается таких простых алгебраических выражений, как в §6.3. Как следствие, для устойчивости линейных систем первого и второго порядка с запаздыванием, оказывается, уже недостаточно только положительности коэффициентов, а для систем третьего и более высокого порядка с запаздыванием неприменимы критерии
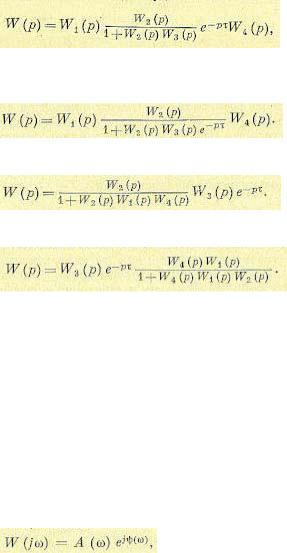
устойчивости Вышнеградского, Рауса и Гурвица.
Ниже будет рассмотрено определение устойчивости только по критерию Найквиста, так как его использование для этой цели оказывается наиболее простым.
Построение амплитудно-фазовой характеристики и исследование устойчивости по критерию Найквиста лучше всего производить, если передаточная функция разомкнутой системы представлена в виде (14.72). Для получения этого необходимо произвести соответствующим образом размыкание системы.
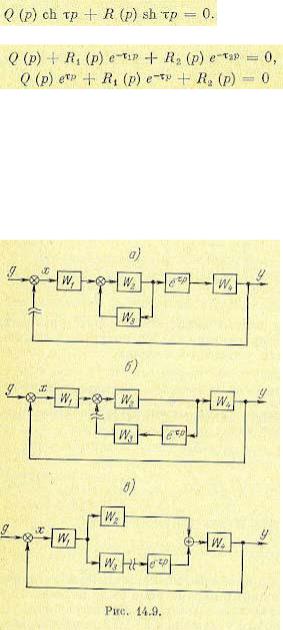
Для случая, изображенного на рис. 14.9, а, размыкание можно сделать в любом месте главной цепи, например так, как это показано. Тогда передаточная функция разомкнутой системы будет
что совпадает по форме с (14.72).
Для случая, изображенного на рис. 14.9, б, размыкание главной цепи дает выражение передаточной функции разомкнутой системы, неудобное для дальнейших исследований:
В этом случае удобнее разомкнуть систему по цепи местной обратной связи. Тогда передаточная функция разомкнутой системы приобретает вид, совпадающий с (14.72):
Наконец, в случае, изображенном на рис. 14.9, в, при размыкании системы в указанном месте получаем выражение, также совпадающее с (14.72):
Заметим, что при наличии характеристического уравнения, записанного в виде (14.70), передаточная функция разомкнутой системы может быть записана сразу в виде (14.72), без нахождения места размыкания на структурной схеме. Записанное в таком виде выражение может быть использовано далее для исследования устойчивости. Частотную передаточную функцию (14.72) можно представить в виде
 (14.73)
(14.73)
Кроме того,
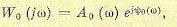 (14.74)
(14.74)
где А0 (w) — модуль и ψ0 (w) — фаза (аргумент) системы без запаздывания. Модуль второго сомножителя (14.73) равен единице, а его аргумент равен ∆ψ = wτ . Поэтому, представив выражение (14.72) в виде
получаем значение модуля результирующей частотной передаточной функции
 (14.75)
(14.75)
и фазы
 (14.76)
(14.76)
Таким образом, наличие звена с запаздыванием не меняет модуля и вносит только дополнительный фазовый сдвиг.

На рис. 14.10 изображена амплитудно-фазовая характеристика, соответствующая (14.74). Сплошной линией показана исходная характеристика при τ = 0 , а пунктиром - характеристика, которая получается при наличии постоянного запаздывания τ ≠ 0 .
Из этих характеристик видно, что наличие дополнительного фазового сдвига ∆ψ = wτ
«закручивает» годограф, особенно в высокочастотной части, по часовой стрелке. Это, вообще говоря, ухудшает условия устойчивости, так как вся кривая приближается к точке (-1, j0). Иногда в особых случаях, при сложной форме годографа W0 (jw), введение постоянного запаздывания может улучшить условия устойчивости.
По имеющемуся годографу W0 (jw) можно определить критическое значение времени запаздывания τ =τср , при котором система оказывается на границе колебательной
устойчивости.
Для этой цели на годографе Ж0 (/со) отыскивается точка, для которой модуль равен единице (рис. 14.10). Частоту, соответствующую этой точке, обозначим w1, а фазу — −ψ1 . При введении постоянного запаздывания τ =τкр . условие совпадения этой точки с
точкой ( — 1, j0) запишется следующим образом:
откуда критическое значение запаздывания
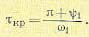 (14.77)
(14.77)
Если подобных «опасных» точек будет несколько, то необходимо сделать расчеты для всех точек и взять наименьшее значение ткр.
Заметим, что частота w1 равна частоте среза л. а. х., w1 = wср (см., например, рис. 4.10 или 6.25). Поэтому нахождение w1 и ψ1 удобно делать при наличии построенных л. а. х. и
л. ф. х. В этом случае, вообще, расчеты по определению устойчивости могут совмещаться с определением качества, системы частотными методами.
Л. а. х. системы с запаздыванием совпадает с л. а. х. исходной системы (без запаздывания). Дополнительный фазовый сдвиг, который надо учесть при построении л. ф. х. системы с запаздыванием, определяется (14.76). В некоторых случаях могут

использоваться аналитические расчеты. Так, например, рассмотрим статическую систему с одной постоянной времени. Частотная передаточная функция разомкнутой системы имеет вид
 (14.78)
(14.78)
Приравняем модуль единице:
Отсюда находится частота, соответствующая опасной точке:
Фазовый сдвиг на этой частоте
По формуле (14.77) находим критическое запаздывание:
 (14.79)
(14.79)
По этому выражению на рис. 14-11 построена область устойчивости в координатах «общий коэффициент усиления — относительное запаздывание».
Рассмотрим более сложный случай астатической системы с одной постоянной времени, когда частотная передаточная функция разомкнутой системы имеет вид
 (14.80)
(14.80)
Приравняем модуль единице:
Отсюда находится частота, соответствующая опасной точке:
Фазовый сдвиг на этой частоте
Критическое запаздывание на основании формулы (14.77)
 (14.81)
(14.81)
Если Т = 0, то из последней формулы, сделав предельный переход, находим
 (14.82)
(14.82)
Пусть К =10 сек-1 и T =0,2 сек. Тогда критическое запаздывание, при котором система теряет устойчивость,
а при Т =0
Оценку качества регулирования в системах с запаздыванием удобнее всего производить при помощи частотных критериев качества (§ 8.5 и § 8.9). Запас устойчивости можно определять по величине показателя колебательности, а быстродействие — по полосе пропускания. Как и в случае систем без запаздывания, заданное значение показателя колебательности будет получено, если амплитудно-фазовая характеристика разомкнутой
системы, построенная по выражению (14.73), не будет заходить в запретную зону, окружающую точку (—1, j0), что изображено на рис. 8.27. Для расчета могут применяться логарифмические характеристики (рис. 8.30).
Построение переходных характеристик удобнее всего производить при помощи вещественных частотных характеристик (§ 7.5).
Для построения переходного процесса могут применяться графические и численнографические методы, а также вычислительные машины.

ГЛАВА 15. ИМПУЛЬСНЫЕ СИСТЕМЫ
§ 15.1. Общие сведения
Линейной системой импульсного регулирования называется такая система автоматического регулирования, которая кроме звеньев, описываемых обыкновенными линейными дифференциальными уравнениями, содержит импульсное звено, преобразующее непрерывное входное воздействие в равноотстоящие друг от друга по времени импульсы.
Вкачестве импульсного звена (элемента) может использоваться падающая дужка гальванометра (рис. 1.28), генерирующая прямоугольные импульсы (рис. 15.1), у которых либо высота (рис. 15.1, а), либо ширина (рис. 15.1, б) пропорциональна непрерывной величине, поступающей на это звено в момент времени, совпадающий с началом импульса.
Кроме того, импульсным звеном может служить устройство типа ключа, которое (как и падающая дужка) по какой-то внешней причине производит замыкание цепи короткими импульсами через равные промежутки времени. Отличие импульсного звена типа ключа от импульсного звена типа падающей дужки состоит в том, что оно «вырезает» определенные участки из непрерывно изменяющегося воздействия (рис. 15.1, в). И те и другие импульсные звенья могут быть осуществлены различными электромеханическими или электронными устройствами. Будем называть их соответственно импульсными звеньями типа I, типа II и типа III (рис. 15.1, а, б, в).
Вкачестве примера возьмем импульсную систему автоматического регулирования температуры 6 (рис. 1.27). Структурная схема ее дана на рис. 15.2, а. Регулируемым объектом может являться, например, тепловой двигатель, температура в котором 6 должна поддерживаться постоянной путем изменения положения ξ =ϕ шторок (регулирующего
органа), т. е. путем изменения интенсивности охлаждения двигателя.
В общем случае любая импульсная линейная система регулирования будет содержать ряд непрерывных звеньев, описываемых обыкновенными линейными дифференциальными уравнениями, и хотя бы одно прерывное — импульсное звено. Поэтому можно изобразить обобщенную структурную схему импульсной системы регулирования так, как показано на рже. 15.2, б, где все непрерывные звенья сведены в один блок — непрерывную часть системы. Последняя может иметь какую угодно структуру (любой сложности, с обратными связями и т. п.). В данном примере в линейную часть входят: приводной двигатель, регулирующий орган (шторки), регулируемый объект и чувствительный

элемент (термометр сопротивления с гальванометром). В качестве импульсной системы можно также рассматривать системы регулирования с управляющими цифровыми вычислительными машинами (ЦВМ). Дискретный характер получения и обработки информации в ЦВМ приводит к так называемому квантованию по времени, что и позволяет применить здесь теорию импульсных систем. Однако системы с ЦВМ оказываются более сложными вследствие так называемого квантования по уровню, что делает их нелинейными. Поэтому теория импульсных систем в случае использования ЦВМ применима только для приближенных исследований, когда задача может быть линеаризована. Более подробно системы с ЦВМ будут рассмотрены в главе 24. Импульсные фильтры. Ограничимся случаем, когда на выходе импульсного элемента импульсы отстоят друг от друга на одинаковые интервалы времени, продолжительность их также одинакова и они отличаются друг от друга только по амплитуде (тип I и тип III
на рис. 15.1).
Импульсная система может быть схематически представлена в виде соединения импульсного звена и непрерывной части. Последовательность импульсов на выходе импульсного звена после прохождения через непрерывную часть вследствие сглаживающих свойств последней превращается в непрерывные величины на выходе. Обычно схема импульсной системы такова, что сигнал ошибки, полученный в элементе сравнения, поступает затем на импульсный элемент (рис. 15.3). Импульсное звено на этой схеме изображено условно в виде ключа, который замыкается с периодом Т. Если время замыкания ключа мало по сравнению с периодом чередования Т и постоянными времени непрерывной части и если сигнал на входе ключа в течение времени, когда он замкнут, практически постоянен, то последовательность конечных по продолжительности импульсов на выходе ключа можно заменить последовательностью дельта-функций. Величина каждой дельта-функции (точнее, интеграла от нее по времени) будет пропорциональной значению сигнала на входе ключа в момент его замыкания.
Поскольку ключ замыкается в определенные моменты времени (О, Т, 2Т, ЗТ и т. д.), то сигнал на входе необходимо рассматривать именно в эти моменты времени. Хотя на выходе непрерывной части сигнал и непрерывен, будем рассматривать его только в отдельные дискретные моменты времени.
Непрерывную часть совместно с ключом на ее входе будем называть импульсным фильтром (рис. 15.4). Более строго импульсный фильтр следует определить как устройство, которое получает входные сигналы и одновременно дает выходные сигналы лишь в определенные моменты времени, например Т, 2Т, ЗТ и т. д. На входе непрерывной части с передаточной функцией Wо (р) действует дискретная функция х*[nТ], где n = 0, ±1, ±2, ±3 и т. д.
В соответствии со сказанным эта функция может быть представлена в виде последовательности дельта-функций.

На выходе будет непрерывная функция, определяемая в эти же дискретные моменты времени: у (t) = у [nТ], где n = 0, +1, ±2 и т. д.
Решетчатые функции. Введем понятие решетчатой функции времени f[nТ], или в сокращенной записи f[n], значения которой определены в дискретные моменты времени t= nТ, где n — целое число, а Т — период повторения. Операция замены непрерывной функции решетчатой
показана на рис. 15.5. Изображенные на рис. 15.5, б ординаты представляют собой так называемые дискреты исходной непрерывной функции f(t) при t = nТ (рис. 15.5, а). Дискреты f(t) могут быть также определены для смещенных моментов времени t = nТ + ∆t = (n +ε )Т. Смещение ∆T = const может быть положительной или отрицательной величиной при выполнении условия ∆T < Т. Относительное смещение ε = ∆T T1 по модулю меньше единицы.
Образование смещенной решетчатой функции f[nТ, ∆T ], или в сокращенной записи f[n,е], из непрерывной функции f(t) для случая ∆T >0 изображено на рис. 15.5, в.
В последующем изложении будем считать, что в решетчатой функции f[n, ε ] аргумент n>0 и параметр ε >0. В случае необходимости рассмотрения функции f[n, ε 0] с отрицательным параметром ε 0 < 0 дискретное время можно представить в виде [(n-1) + +(1+ ε 0)] Т = [(n- 1) + ε ]T. Тогда решетчатая функция может быть записана в виде f[n-1,
ε ], где ε = 1 + ε 0.
Решетчатая функция не обязательно должна формироваться из некоторой исходной непрерывной. Любая числовая последовательность некоторой величины, определенная в дискретные равноотстоящие моменты времени, может быть представлена в виде решетчатой функции.
Заметим, что обратная задача — формирование непрерывной функции из решетчатой — не может быть решена однозначно, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций. Это показано на рис. 15.6. Непрерывные функции, совпадающие с заданными дискретами,

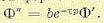 (14.56)
(14.56) (14.57)
(14.57) (14.58)
(14.58) (14.59)
(14.59)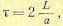 (14.60)
(14.60)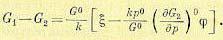 (14.61)
(14.61)