Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

называются огибающими решетчатой функции. Так, например, огибающая может быть изображена в виде ступенчатой функции (кривая 3 на рис. 15.6).

Введем также понятие основной огибающей функции. Под основной огибающей будем понимать непрерывную функцию, совпадающую с заданными дискретами, которая может быть получена как результат решения дифференциального уравнения, порядок которого наименьший по сравнению с другими возможными огибающими, а для периодических решетчатых функций,

Кроме того, выполняется требование минимальности значений частот гармоник. Так, например, решетчатой функции e−αnT могут соответствовать огибающие e−αt и

e−αt (cos w0t + β sin w0t) , где w0 2kT −1 , k — целое число, β — любое число. Однако первая

из них (основная огибающая) может быть получена в результате решения дифференциального уравнения первого порядка, тогда как вторая — в результате решения дифференциального уравнения второго порядка.

Аналогом первой производной непрерывной функции для решетчатой функции является либо первая прямая разность

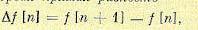(15.2)

либо первая обратная разность

(15.3)

Обе эти разности показаны на рис. 15.7. Разности могут быть определены и для смещенных решетчатых функций f[n, ε ]. Однако формулы для ε ≠ 0 и ε = 0 здесь и далее оказываются идентичными, вследствие чего в дальнейшем изложении принято ε =0. Прямая разность определяется в момент времени t= nТ по будущему значению решетчатой функции при t = (n + 1)Т. Это можно сделать в тех случаях, когда будущее значение известно.

Обратная разность определяется для момента времени t=nТ по прошлому значению решетчатой функции в момент времени t = (n — 1)T.

Аналогом второй производной непрерывной функции для решетчатой функции служат вторые разности: прямая

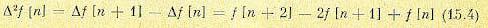(15.4)

и обратная

(15.5)

Приведенные выше замечания относительно возможности вычисления прямой и обратной разностей сохраняют свою силу и здесь.

Могут определяться и высшие прямая и обратная разности. Для вычисления k-й разности возможно использование рекуррентных соотношений

(15.6)

(15.7)

или формул общего вида

(15.8)

(15.9)

где биномиальные коэффициенты (число сочетаний)

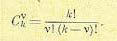(15.10)

Обратные разности обладают важной особенностью. Если решетчатая функция определена только для положительных значений аргумента, т. е. f[n] = 0 при n< 0, то, как следует из (15.9), в точке n=0 k-я разность

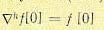(15.11)

для любого целого положительного k.

Аналогами интеграла непрерывной функции в пределах от 0 до t для решетчатой функции являются неполная сумма

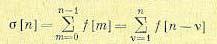(15.12)

и полная сумма

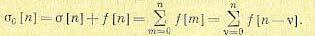(15.13)

Отличие (15.13) от (15.12) заключается в том, что значение f[n] в момент времени t= nТ также участвует в формировании результата.

Разностные уравнения. В качестве аналогов дифференциальных уравнений можно рассматривать разностные уравнения (уравнения в конечных разностях). При использовании прямых разностей неоднородные линейные разностные уравнения имеют вид

(15.14)

где f[n] — заданная, а у[n] — искомая решетчатые функции. При f[n] = 0 уравнение (15.14) становится однородным разностным уравнением, решением которого будет y[n]. При использовании (15.8) разностное уравнение (15.14) можно записать в другом виде:

(15.15)

Коэффициенты этого уравнения определяются из зависимости

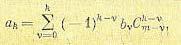(15.16)

где биномиальные коэффициенты

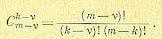(15.17)

При использовании обратных разностей уравнение в конечных разностях будет

(15.18)

С учетом формулы (15.9) последнее выражение приобретает вид

(15.19)

Коэффициенты последнего уравнения определяются выражениями

(15.20)

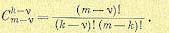(15.21)

Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие вычислять значения у[n + m] при n— 0, 1, 2, ... для заданных начальных значений y [0], у [1], . . ., y [m— 1] и уравнения вида (15.15) или значения у[n] при n = 0, 1, 2, ... для заданных начальных значений у[n —m], у[n —m+ 1], . . ., у [n — 1] и уравнения вида (15.19). Такие вычисления легко машинизируются, а также не представляют никаких принципиальных трудностей и при ручном счете (кроме, конечно, затрат времени) даже в случае, когда коэффициенты разностных уравнений ai (i = О, 1, . . ., m) с течением

времени изменяются. Это отличает разностные уравнения от их непрерывных аналогов — дифференциальных уравнений.

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

(15.22).

где z(i= 1, 2, . . ., m) — корни характеристического уравнения

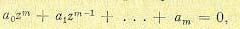(15.23)

а Сi — произвольные постоянные.

Из (15.22), в частности, вытекает условие того, чтобы свободное движение системы, описываемой разностным уравнением (15.15), было бы затухающим (условие устойчивости):

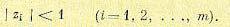(15.24)

Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, w-преобразование, а также частотные методы, которые будут изложены ниже.

§ 15.2. Использование z-преобразования

Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа, определяемое формулой

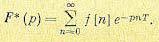(15.25)

Для смещенных решетчатых функций может быть записано аналогичное выражение:

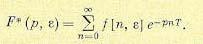(15.26)

Формулы (15.25) и (15.26) можно представить в символической записи аналогично (7.20):

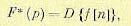(15.27)

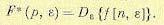(15.28)

В приведенных формулах, как и в случае непрерывного преобразования Лапласа, комплексная величина р = с + jw, где с — абсцисса абсолютной сходимости. Если с < ∞, то ряд, определяемый формулами (15.25) и (15.26), сходится и решетчатой функции соответствует некоторое изображение.

Как следует из (1:5.25) и (15.26), изображение решетчатой функции является функцией величины ерТ. Для смещенных решетчатых функций в изображение будет входить, кроме того, параметр ε .

Для исследования импульсных систем большое распространение получило так называемое z-преобразование, которое связано с дискретным преобразованием Лапласа и вытекает из него. Применительно к z-преобразованию ниже будут рассмотрены основные свойства и теоремы дискретного преобразования Лапласа.

Под z-преобразованием понимается изображение несмещенной или смещенной решетчатых функций, определяемое формулами

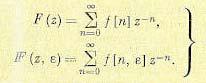(15.29)

В этих формулах введено новое обозначение z= ерТ. Из них следует, что z-преобразование практически cовпадает с дискретным преобразованием Лапласа и отличается только обозначением аргумента изображения.

Таким образом, решетчатая функция времени (оригинал) заменяется ее изображением (z- преобразованием). Формулы преобразования (15.29) могут быть записаны в символической форме:

(15.30)

Формулы преобразования (15.30) могут быть записаны и для непрерывной производящей функции в виде

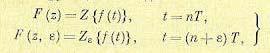(15.31)

где n=0, 1, 2, ...

Ряды (15.29) сходятся, и изображение решетчатой функции существует, если выполняется условие, сформулированное выше для дискретного преобразования Лапласа: с < ∞, где с

— абсцисса абсолютной сходимости.

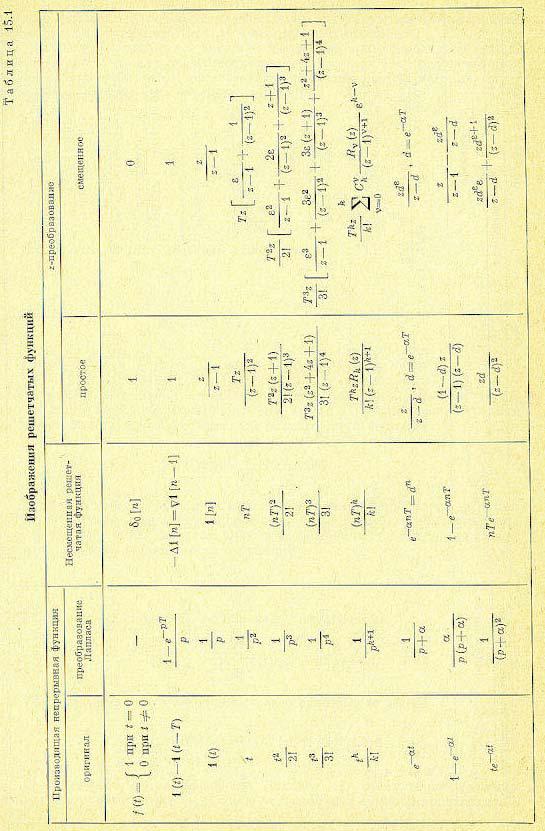
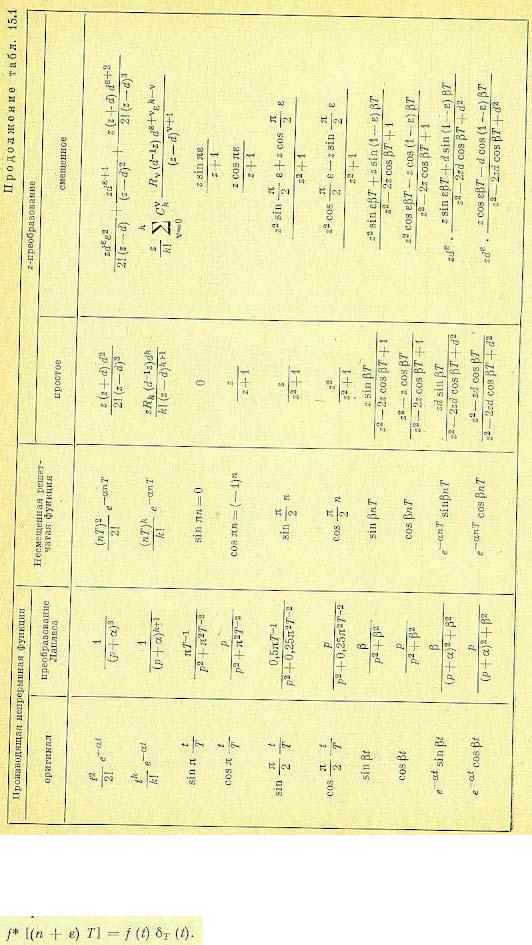
Втабл. 15.1 приведены изображения некоторых решетчатых функций, а также производящих функции времени и их изображений Лапласа.

Втаблице введена единичная импульсная решетчатая функция [68].

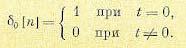(15.32)

Эта функция играет в дискретных системах такую же важную роль, как δ -функция (функция Дирака) в непрерывных системах.

Для всех непрерывных и решетчатых функций, приведенных в табл. 15.1, предполагается, что они тождественно равны нулю при t< 0. В некоторых изображениях табл. 15.1 использованы полиномы Rk (z), которые могут быть представлены в виде определителя

[136]

(15.33).

Некоторые частные значения этого полинома:

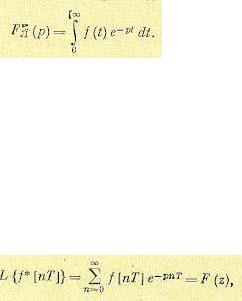
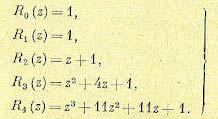(15.34)

Операцию нахождения z-преобразования от решетчатой функции (15.30) или от непрерывной производящей функции (15.31) можно распространить на изображение Лапласа непрерывной производящей функции

Пусть решетчатая функция f[nТ] получается из непрерывной функции f(t) квантованием в моменты времени t = nТ. Введем вспомогательную импульсную функцию, образованную умножением исходной непрерывной функции на последовательность δ -функций

(15.35).

Найдем преобразование Лапласа введенной функции

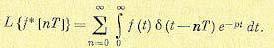(15.36).

Так как интеграл от δ -функции равен единице, то имеем

где z= ерт.

Таким образом, преобразование Лапласа для импульсной функции оказывается равным z- преобразованию исходной непрерывной производящей функции.

Обозначив последовательность δ -функций вида δ(t − nt −εt) , где n— 0, 1, 2, . . ., через δT (t) , импульсную функцию при ε ≠ 0 , можно представить следующим образом: '

(15.38)

Применим к левой и правой части последнего выражения преобразование Лапласа. В соответствии с приведенным доказательством в левой части будет получено z- преобразование исходной непрерывной функции времени

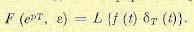(15.39)

Используем далее теорему свертки в комплексной области

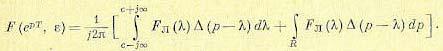(15.40)

Здесь Fл(р) = L{f(t)}. Кроме того,

а также

Интегрирование в (15.40) ведется по прямой р = с + jw, где с — число,

большее абсциссы абсолютной сходимости, и по полуокружности радиуса R → ∞. Полуокружность может быть выбрана как в левой, так и в правой части комплексной плоскости. В последнем случае внутрь контура интегрирования

попадают полюсы подынтегрального выражения, определяемые равенством e−( p−λ)T =1 или − ( p − λ)T = j2πr , где r = 0, ±1, ±2, . . .Значение полюса λr = p + jr 2Tπ .

Для вычисления интеграла удобно обозначить

'Тогда искомый интеграл можно представить в виде

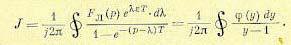(15.41)

Для каждого из полюсов в соответствии с теоремой Коши можно записать

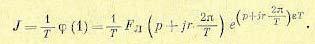(15.42)

Окончательное выражение для искомого z-преобразования будет при

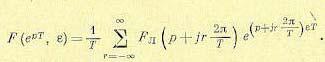(15.43)

Эта формула справедлива при любом значении ε > 0. Однако при ε = 0 она становится неверной, так как начальный момент времени становится моментом квантования. Для этого случая можно показать [136], что z-преобразование должно вычисляться в соответствии с выражением

(15.44)

Операцию нахождения z-преобразования по преобразованию Лапласа символически можно записать, аналогично формулам (15.30) и (15.31), в виде

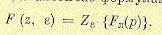(15.45)

Формулы (15.43) и (15.44) имеют больше теоретическое, чем практическое значение. В большинстве случаев нахождение z-преобразования для изображения Лапласа Рл(р) проще

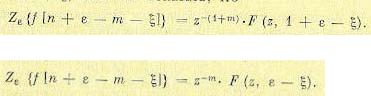
осуществить переходом к оригиналу f(t) известными методами и использованием затем табл. 15.1.

Рассмотрим кратко основные правила и теоремы применительно к z-преобразованию. Эти же правила и теоремы будут справедливыми и для дискретного преобразования Лапласа. Рассмотрение проведем для несмещенных решетчатых функций, но полученные результаты можно распространить и на случай смещенных функций f[n, ε ], кроме случаев, оговоренных особо.

1. Свойство линейности. Это свойство заключается в том, что изображение линейной комбинации решетчатых функций равно той же линейной комбинации их изображений. Пусть решетчатая функция определяется выражением

(15-46)

Тогда для ее изображения можно записать

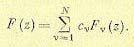(15.47)

2. Теорема запаздывания и упреждения. Рассмотрим решетчатую функцию f[n — m],

сдвинутую вправо (запаздывающую) на целое число тактов m. Тогда из формулы (15.29) следует, если обозначить n — m = r,

(15.48)

Здесь F(z) — изображение функции f[n]. Если исходная решетчатая функция f[n] равна нулю при отрицательных значениях аргумента, то формула (15.48) упрощается:

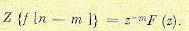(15.49)

Если сдвиг функции f[n] происходит влево (упреждение) и рассматривается функция f[n+m] , где m— целое положительное число, то аналогично случаю запаздывания можно показать, что

(15.50)

Второе слагаемое в правой части (15.50) обращается в нуль, если f[n] = 0 при n = 0, 1, . . ., m-1.

При запаздывании на не целое число периодов m +ξ приходится вводить смещенную

3. Теорема об умножении оригинала на экспоненту (теорема смещения в области изображений). Умножим решетчатую функцию на экспоненту еλ nТ. Тогда из формулы

(15.29) следует:

(15.53)

Для смещенной решетчатой функции аналогичная формула имеет вид

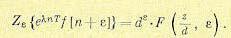(15.54)

4. Теорема об умножении оригинала на степенную функцию. Пусть решетчатой функции f[n] соответствует изображение F(z). Тогда можно показать, что

(15-55)

Для смещенной решетчатой функции аналогичная зависимость имеет вид.

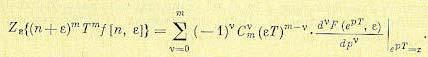(15.56)

5. Изображение разностей. Для первой прямой разности на основании (15.50)

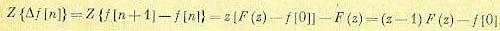(15.57)

Если k — целое число, то аналогичным образом

(15.58) причем ∆0 f [0] = f [0] .

Если решетчатая функция f[n] равна нулю в первых k точках оси времени, т. е. f[0] = f[1] =...=f[k— 1] = 0, то формула (15.58) упрощается:

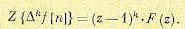(15.59)

Для первой обратной разности можно аналогичным образом найти

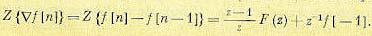(15.60)

Если для отрицательных аргументов решетчатая функция тождественно равна нулю, то формула (15.60) упрощается:

(15.61)

Для k-й обратной разности при f[n] = 0 для n<0

(15.62)

Полученные формулы изображений прямых и обратных разностей формально напоминают формулы для нахождения изображений производных непрерывных функций. Формула (15.62) аналогична случаю изображения производной k-го порядка непрерывной функции по начальным условиям слева при нулевых их значениях. Заметим, что при Т→0 (непрерывный случай) множитель в правой части стремится к пределу:

(15.63)

К такому же пределу стремится множитель (z — 1)k в (15.59). Это также иллюстрирует сходство формул изображений производных и разностей.

6. Изображение сумм. Рассмотрим вначале неполную сумму (15.12):

Составим первую прямую разность этой суммы