
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf
 (18.42)
(18.42)
и эти две кривые нанесем на тех же графиках. Теперь остается на этих двух кривых найти такие точки С и В, в которых кривые Z1 (w) и Z2 (w) пересекают линии с одинаковыми значениями а при одном и том же значении w. Полученные величины а и w будут решением задачи, т. е. амплитудой ап и частотой wп искомого периодического решения. Во многих встречающихся на практике задачах вместо (18.41) будет
 (18.43),
(18.43),
Тогда кривые q и q' на рис. 18.6 для разных амплитуд будут иметь вид горизонтальных прямых линий.
В простейшем случае, когда в системе имеется однозначная нечетно-симметричная нелинейность F(х), для которой q = q(а) и q' = 0, из уравнений (18.40) можно найти
 (18.44)
(18.44)
Тогда, исключив q из уравнений (18.40), найдем частоту w = wп как функцию параметров системы. Затем, изобразив график зависимости д (а) (рис. 18.7), проведем на нем согласно (18.44) горизонтальные линии q =Z(w) для разных постоянных значений w= wп, т. е. для разных соотношений параметров системы. Точки пересечения этих прямых (w = wп) с кривой q(а) (например, на рис. 18.7 точки ап1 и ап2) определяют в каждом случае амплитуды периодических решений,. Если пересечений нет, то и периодических решений в системе не будет. В простейших случаях уравнение (18.44) решается аналитически.
Графический способ. Для гармонически линеаризованного характеристического уравнения (18.33) можно написать выражение кривой Михайлова
 (18.45)
(18.45)
где знак — введен, чтобы отличать текущий параметр w, изменяющийся вдоль кривой Михайлова, от частоты w, входящей в выражение гармонической линеаризации нелинейности.


Из двух уравнений (18.48) и(18.49) определяются неизвестные амплитуда ап и частота wп автоколебаний, входящие в состав коэффициентов (18.47). При этом точно так же, как в основном способе, здесь на основании уравнений (18.48) и (18.49) можно строить графики зависимостей ап и wп от одного параметра системы или на плоскости двух параметров с целью их выбора.
Если гармонически линеаризованное уравнение (18.33) нелинейной системы имеет четвертую степень относительно р:
 (18.50)
(18.50)
то условие наличия пары чисто мнимых корней согласно § 6.2 будет
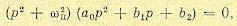 (18.51)
(18.51)
Кроме того, записывая уравнение (18.50) в виде раскрывая здесь скобки и приравнивая полученные коэффициенты соответствующим коэффициентам (18.50), находим
 (18.52)
(18.52)
С помощью двух уравнений (18.51) и (18.52) решаются все вышеуказанные задачи для нелинейной системы четвертого порядка.
Заметим, что для систем с нелинейностью вида х2 = F(х1) без гистерезисной петли частота со не входит в коэффициенты характеристического уравнения. Поэтому из уравнения (18.48) или (18.51) сразу определяется амплитуда ап, а затем из (18.49) или (18.52) — частота wп. Для систем с более сложными нелинейностями получаются два уравнения с двумя неизвестными.
Учет временного запаздывания в нелинейной системе. В нелинейной системе, как и в линейной, может иметься постоянное по времени запаздывание τ .
При этом уравнение линейной части (18.31) получит вид
Выражение (18.34) при этом будет
 (18.53)
(18.53)
К уравнению (18.53) можно применить основной способ отыскания периодических решений или другой из изложенных выше.
Устойчивость периодических решений. Выше уже указывалось, что не всякое периодическое решение уравнений собственного движения нелинейной системы будет соответствовать автоколебаниям, а только устойчивое. В конкретных задачах часто из физических соображений бывает сразу видно, возникают автоколебания или нет. Поэтому иногда нет нужды в математическом исследовании устойчивости найденного периодического решения. Однако в ряде случаев все же приходится этот вопрос исследовать.
Задача исследования устойчивости периодического решения сводится, вообще говоря, к анализу линейного уравнения с периодическими переменными коэффициентами. А. М. Ляпуновым [82] разработаны соответствующие методы. Но их использование во многих случаях представляет пока еще большие трудности. Поэтому здесь строгое исследование устойчивости периодических решений излагаться не будет.
Опишем три приближенных способа исследования устойчивости периодического решения: 1) осреднение коэффициентов, 2) использование кривой Михайлова, 3) аналитический критерий.
Осреднение коэффициентов при исследовании устойчивости периодического решения. Запишем дифференциальное уравнение замкнутой системы в малых отклонениях ∆x : от исследуемого периодического решения: х =ап sinwп. Для линейной части системы на основании уравнения (18.31) получим

 (18.54)
(18.54)
Уравнение нелинейного звена, например х2 =F(x1, px1), примет при этом для малых отклонений вид
(аналогично и для других типов нелинейных уравнений), где индекс «п» означает, что в частные производные нужно подставить х2 = ап sinwпt и рх1= апwпcoswпt. Эти частные производные и являются периодическими переменными коэффициентами. В задачах теории регулирования они могут меняться как плавно, так и скачками (см. примеры в § 18.3). Осредним полученные периодические коэффициенты, после чего вместо (18.55) будем иметь линейное уравнение с постоянными коэффициентами
 (18.56)
(18.56)
где
 (18.57)
(18.57)
Характеристическое уравнение системы, определяющее устойчивость периодического решения, согласно (18.54) и (18.56) будет
 (18.58)
(18.58)
Если оно удовлетворяет линейному критерию устойчивости, то исследуемое периодическое решение устойчиво.
В случаях, когда нелинейное звено описывается уравнением вида х2= F(х1) (с гистерезисной петлей или без нее), осредненное характеристическое уравнение для исследования периодического решения будет
 (18.59)
(18.59)
где
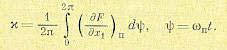 (18.60)
(18.60)
Использование кривой Михайлова для исследования устойчивости периодического решения. Каждому конкретному значению а будет соответствовать определенная кривая Михайлова (18.45). При а = ап она пройдет через начало координат (рис. 18.9).
Для исследования устойчивости периодического решения с амплитудой а = ап дадим малое приращение амплитуде ∆а. Тогда при а =ап + ∆а кривая Михайлова займет либо положение 1, либо положение 2 (рис. 18.9). При этом, как известно из линейной теории (§ 6.3), кривая 1, охватывающая начало координат, соответствует затухающим колебаниям переходного процесса, а кривая 2 — расходящимся колебаниям.
Поэтому, если при ∆а > 0 кривая Михайлова займет положение 1, а при ∆а < 0 - положение 2, то переходный процесс в системе будет таким, что колебания с амплитудой,

большей чем ап, затухают, а колебания с амплитудой, меньшей чем ап, расходятся. Следовательно, переходный процесс с обеих сторон сходится к исследуемому периодическому процессу с амплитудой ап. Это означает
устойчивость последнего, т. е. в системе имеют место автоколебания. Если же при ∆а >0 получится кривая 2, а при ∆а < 0 — кривая 7, то переходный процесс в обе стороны расходится, т. е. исследуемое периодическое решение неустойчиво (система устойчива в малом и неустойчива в большом, как на рис. 16.3, б).
Аналитический критерий устойчивости периодического решения. Развивая предыдущий способ, видим, что нет необходимости строить сами кривые Михайлова. Все исследование можно произвести аналитически. В самом деле, для того чтобы узнать, примет ли кривая Михайлова при ∆а > 0 положение 1 (рис. 18.9), достаточно определить, куда будет перемещаться с увеличением а та точка кривой Михайлова (w = wп) которая при а = ап находится в начале координат. Если она будет перемещаться по направлениям ОА1, ОА2 или ОА3 (рис. 18.10, а), то периодический процесс с амплитудой: а = ап устойчив, а если по направлениям ОА4 или ОА5 — неустойчив.
Это направление перемещения точки w= wп из начала координат с увеличением а определяется, очевидно, следующими проекциями на координатные оси X и У:
 (18.61)
(18.61)
где X и У обозначают вещественную и мнимую части аналитического выражения кривой Михайлова, а индекс «п» означает подстановку а = ап, w = wп. Как видно из рис. 18.10, а, для устойчивости исследуемого периодического решения вектор, определяемый проекциями (18.61), должен лежать с определенной стороны от касательной МN к кривой Михайлова, направление которой в свою очередь определяется проекциями
 (18.62)
(18.62)
Из расположения вектора с проекциями (18.61) по отношению к вектору с проекциями (18.62) и видна непосредственно устойчивость или неустойчивость данного периодического решения с амплитудой ап.
На рис. 18.10, б и в показаны те же векторы, что и на рис. 18.10, а, но для других видов кривых Михайлова. Видно, что во всех случаях для устойчивости исследуемого периодического решения требуется, чтобы вектор с проекциями (18.61) лежал справа от касательной МN, если смотреть вдоль кривой Михайлова в сторону возрастания со, причем направление касательной MN определяется вектором с проекциями (18.62). Это геометрическое условие устойчивости периодического решения можно записать в следующем аналитическом виде:
 (18.63)
(18.63)
или иначе:


Пусть, например, определено, что периодическое решение, амплитуда которого показана на рис. 18.5, а, устойчиво (оно соответствует автоколебаниям). Условимся факт устойчивости периодического решения обозначать на графике вертикальными стрелками, сходящимися к данному периодическому решению (рис. 18.12, а). Этим обозначением иллюстрируется то, что переходные процессы с обеих сторон (т. е. с большими, чем ап, и с меньшими, чем ап начальными амплитудами) сходятся к автоколебательному процессу с амплитудой ап. Пусть в данном случае k; обозначает коэффициент усиления регулятора. Трафик рис. 18.12, а показывает, что в системе возникают автоколебания при k>kгр. Естественно сделать отсюда вывод о том, что в области 0 < k <kгр (где нет периодического решения) данная система регулирования будет устойчива, что также обозначено на рис. 18.12, а вертикальной стрелкой.
Аналогичное заключение для области 0 ≤k ≤kгр можно сделать и в случае неустойчивого периодического решения на рис..18.12, б, и в случае наличия двух периодических решений на рис. 18.12, в, одно из которых устойчиво, другое неустойчиво. Если же автоколебания наблюдаются в области 0 ≤k ≤kгр, как показано на рис. 18.12, г, то естественно предположить, что область k >kгр будет областью неустойчивости данной нелинейной системы.
Наконец, если периодических решений для исследуемой нелинейной системы не получается вовсе ни при каких значениях ее параметров, то согласно геометрическому способу определения автоколебаний (см. выше) получим, что кривая Михайлова будет либо охватывать начало координат при всяком значении а, либо не охватывать его при всех а. Отсюда можно сделать вывод, что в первом случае данная нелинейная система устойчива, а во втором — неустойчива.
Развитие, а также сравнение данного способа определения устойчивости равновесия нелинейной системы с методом Ляпунова, показывающее эффективность такого способа,
см. в книге [100], §§ 2.7—2.9.
§ 18.3. Примеры исследования нелинейных систем первого класса
Рассмотрим несколько примеров применения изложенного в предыдущем параграфе метода.
Пример 1. Найдем влияние ограничения линейной характеристики двигателя (рис. 18.13, а) на процессы в следящей системе. Пусть остальные звенья системы линейны. Тогда уравнение управляемого объекта с двигателем вместо (16.63) примет вид
где F(iя) определяется графиком рис. 18.13, а. Применяя к правой части этого уравнения формулы гармонической линеаризации (18.22) с заменой с=bkс, получаем уравнение управляемого объекта с двигателем в виде
 (18.65)
(18.65)
где

 (18.66)
(18.66)
что изображено графически на рис. 18.13, б. Здесь а обозначает амплитуду колебаний величины iя.
Общее уравнение остальной части следящей системы согласно (16.53) будет
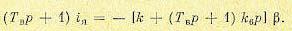 (18.67)
(18.67)
На основании (18.65) и (18.66) получаем характеристическое уравнение
 (18.68)
(18.68)
После приведения его левой части к виду а0р3 + а1p2 + а2р + а3 и подстановки р = jw получаем уравнения типа (18.36) в виде
Выясним влияние параметра k (общего коэффициента усиления) на автоколебания в данной системе. Из последнего уравнения находим
 (18.70)
(18.70)
а из первого
 (18.71)
(18.71)
Формула (18.70) дает график, изображенный на рис. 18.13, в, где
 (18.72)
(18.72)
Графики на рис. 18.13, б и в определяют связь между амплитудой ап частотой wп периодического решения в данной системе.
Найдем зависимость амплитуды ап от величины параметра k. Для этого,
задаваясь различными wп, будем брать из графика рис. 18.13 соответствующие значения ап, а по формуле (18.71) вычислять k. В результате получим график ап (k) типа рис. 18.14, а или 6. Чтобы определить, в каких случаях каждый из них имеет место, найдем kmin. Дифференцируя (18,71) по wп с учетом (18.70) соответствующее значение wм и приравнивая результат в виде
 (18.73)
(18.73)
причем kmin определяется подстановкой ам в (18.70) и (18.71), а именно:
 (18.74)
(18.74)
Сравнивая (18.73) и (18.72), приходим к выводу, что для системы, параметры которой удовлетворяют условию
 (18.75)
(18.75)
справедлив график на рис. 18.14, а, а для системы с параметрами
 (18.76)
(18.76)
— на рис. 18.14, б.
Исследуем устойчивость найденного периодического решения по критерию (18.63). Согласно (18.66) частота со не входит в коэффициенты. Поэтому в выражении (18.45) для кривой Михайлова функции X (w) и У (w) совпадают с (18.69).
Найдем производные:
 (18.77)
(18.77)
так как согласно рис. 18.13, б производная dq/dа отрицательна.
Легко проверить, что при w>wя, где wм определяется формулой (18.73), критерий (18.63) удовлетворяется, а при w<wм не удовлетворяется. Отсюда делаем заключение, что все периодические решения на рис. 18.14, а устойчивы (т. е. соответствуют автоколебаниям). Вертикальными стрелками там показано, что переходные процессы с большими и меньшими амплитудами сходятся к данному периодическому процессу. На рис. 18.14, б только верхняя ветвь кривой (выше точки wм) соответствует устойчивым периодическим решениям, т. е. автоколебаниям, а нижняя (wм -wв) — неустойчивым.
Как уже отмечалось, через ап здесь обозначена амплитуда колебаний величины iя. Чтобы узнать амплитуду ар автоколебаний регулируемой величины р, надо воспользоваться уравнением (18.65), откуда
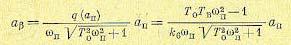 (18.78)
(18.78)
как модуль соответствующей передаточной функции при р = jwп, умноженный на ап. При этом величины ап и wп определяются графиком рис. 18.14, а или б.
Учитывая, что q(а) = k1 при а = b (см. рис. 18.13, б), найдем по формуле (18.71) с подстановкой wп = wв из (18.72) величину kв, отмеченную на рис. 18.14:
 (18.79)
(18.79)
Точно такое же значение Н является .границей устойчивости для линейной системы, когда уравнение управляемого объекта с двигателем вместо (18.65) имеет линейный вид (T1р+1) рβ = k1iя. Отсюда можно сделать вывод о том, что в случае (18.75), для которого имеет
место график рис. 18.14, а, данная нелинейная система сохраняет устойчивость в той же области, что и линейная система, но она обладает еще установившимся автоколебательным режимом там, где линейная система неустойчива. Следовательно, ограничение линейной характеристики типа насыщения в двигателе (рис. 18.13, а) препятствует раскачиванию системы, которое получается при k >kв в линейной системе. Это наблюдается и на практике.
В случае же (18.76), для которого график, определяющий автоколебания, имеет вид рис. 18.14, б, автоколебания могут уже появиться при k< kв (но >kм), т. е. раньше наступления границы устойчивости линейной системы. Но в этом случае, как видно из рис. 18.14, б, при малых начальных амплитудах переходного процесса (ниже кривой wмwв) сохраняется

еще устойчивость равновесного состояния. Здесь в области параметров kм < k< kв (рис. 18.14, б) имеется как бы два предельных цикла (рис. 16.14, б), а в области kв < k < ∞ — один.
Случай, изображенный на рис. 18.14, б, называется «жестким возбуждением» автоколебаний. Такое возбуждение автоколебаний раньше наступления границы устойчивости возможно, как видно из (18.76), только при достаточно большом k6, который, по существу, является коэффициентом гибкой обратной связи. При отсутствии такой связи указанное явление не имело бы места.
На рис. 18.15, а и б даны графики для величины частоты автоколебаний wп в зависимости от параметра k соответственно для случаев, изображенных на рис. 18.14, а и б.
Пример 2. Рассмотрим теперь следящую систему с линейной характеристикой привода, но учтем сухое трение совместно с линейным (рис. 18.16, а). Уравнение управляемого объекта с двигателем имеет при этом вид (16.52). Здесь возможны два случая: 1) колебания без остановок, когда обеспечиваются условия первого из уравнений (16.52); 2) колебания с остановками, когда действуют попеременно оба уравнения (16.52). Рассмотрим первый случай и определим условия его существования.
Итак, записываем первое из уравнений (16.52), поделив его на с2, в виде
 (18.80)
(18.80)
с условием, что
 (18.81)
(18.81)
Обозначим х = p β . Тогда это уравнение будет
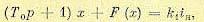 (18.82)
(18.82)
где
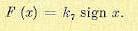 (18.83)
(18.83)
Поскольку движение предполагается без остановок, то нелинейную функцию (18.83) подвергаем гармонической линеаризации, как релейную характеристику, и на основании формулы (18.18), полагая
получаем

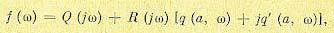 (18.46)
(18.46) (18.47)
(18.47) (18.48)
(18.48)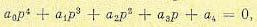 (18.49)
(18.49) (18.64)
(18.64)