Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

Для применения графического метода § 21.1 к отысканию зависимости ав (х°) по уравнению (21.33) нужно на рис. 21.1 построить серию кривых Z(ав) для разных значений х° =const, которые согласно (21.28) входят в выражения для q и q'. Уравнение аналитического метода (21.17) примет вид

(21.35)

где Х2, Y2 и X, Y обозначают вещественные и мнимые части соответственно для выражения Z2 (wв) и выражения

Уравнение (21.35) не решается так просто, как (21.17). Однако можно применить следующий графический прием его решения. Разбив (21.35) на два уравнения:

построим по первому из них на плоскости (ξ ав) кривую 1 (рис. 21.7), а по второму —

серию кривых 2 для разных значений х° =const при заданных В и wв. Перенося полученные точки пересечения кривых вправо на плоскость x°, ав, получаем сразу искомую зависимость ав (x°) для заданного внешнего периодического воздействия, т. е. для заданной пары значений В и wв. Эту зависимость легко получить таким же путем и для любых других заданных В и wв.

Подставив теперь значение амплитуды ав в первое из выражений (21.29), найдем функцию смещения в виде

(21.36).

которая является характеристикой данного нелинейного звена системы по отношению к медленно меняющимся составляющим переменных F и х. Эти медленно меняющиеся составляющие определяются затем путем решения дифференциального уравнения (21.31), в которое надо подставить найденную функцию смещения (21.36).

Независимость очертания функции смещения Ф (х°) от характера изменения и места приложения медленно меняющихся внешних воздействий здесь остается в силе, как было и при автоколебаниях (глава 19).

Однако принципиальным отличием функции смещения (21.36), определяющей прохождение медленно меняющихся сигналов через нелинейную систему при наличии вынужденных колебаний, от функции смещения (19.13) при автоколебаниях является существенная зависимость ее от частоты и амплитуды внешнего периодического воздействия (в то время как при автоколебаниях вид функции смещения зависел только от

.структуры и от соотношения параметров самой системы).

В результате для каждой заданной частоты вынужденных колебаний сов получается серия кривых F° = Ф (х°) для разных значений амплитуды В внешнего периодического

воздействия f2(t), как показано, например, на рис. 21.8, а-. При заданных сов и В получается вполне определенное очертание функции смещения Ф (x°), зависящее только от структуры и параметров самой системы, входящих в уравнение (21.33).

Здесь, так же как и в главе 19, возможен и второй метод отыскания функции смещения. При этом методе попутно определяются также статические и установившиеся ошибки. Метод состоит в следующем.

Поскольку функция смещения F0 = Ф (x°) не зависит от характера изменения и места приложения медленно меняющихся воздействий, то ее можно определить для простейшего случая f1= const = f10 (или при астатической системе для pf1= const = f10). Тогда уравнение (21.31) принимает вид

(21.37)

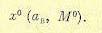(21.39)

Подставив это в выражения для q и q', определяемые второй и третьей из формул (21.29), получим зависимости

Вводя их в уравнение (21.33), эквивалентное (21.32), и решая его любым из двух способов, указанных -выше, при заданных В и wв находим амплитуду вынужденных колебаний ав(М°). Подставляя ав (М°) в (21.38) и (21.39), получаем зависимости

(21.40)

Эти зависимости представляют самостоятельный интерес, так как ими определяется статическая ошибка (а для астатической системы — установившаяся ошибка при постоянной скорости) нелинейной системы Mо медленно меняющейся составляющей, на которую накладывается еще установившаяся периодическая ошибка вынужденных колебаний с амплитудой ав (М°). Все эти ошибки определяются, как видим, в зависимости от величины постоянной правой части М° уравнения (21.37), т. е. от величины внешнего

воздействия (постоянного и равного f1 или меняющегося с постоянной скоростью g1). Но, кроме того, что очень важно для нелинейных систем, величина статического отклонения х° (М°) может существенно зависеть от амплитуды В и частоты wв внешнего периодического воздействия, так как выражения (21.40) ;выводились с помощью уравнения (21.33), в которое входят В и wв. В свою очередь амплитуда вынужденных колебаний ав зависит через М° от величины постоянного внешнего воздействия. Это яркий пример неприменимости принципа суперпозиции для нелинейных систем и в то же время иллюстрация достоинства развиваемого здесь метода, который позволяет это уловить, несмотря на приближенность решения задачи.

Далее, исключая из выражений (21.40) величину М°, находим функцию смещения F°=Ф(х°) для заданных В и wв (рис. 21.8, а).

Итак, наличие в нелинейной системе вынужденных колебаний с частотой внешнего периодического воздействия приводит к эффекту вибрационного сглаживания нелинейности, как и при автоколебаниях. При этом согласно (21.31) для медленно протекающих процессов в условиях вынужденных вибраций исходное дифференциальное уравнение системы (21.24) заменяется уравнением

(21.41)

т. е. заданная нелинейность F(х, рх) заменяется функцией смещения Ф (х°) и отбрасывается внешнее периодическое воздействие f2 (t), по сравнению с которым f1 (t) является медленно меняющимся.

Функция смещения Ф (х°) обычно на определенном участке изменения величины хй изображается однозначной плавной кривой (рис. 21.8. а), в то время как заданная нелинейность F(х, рх) или F(х) может быть скачкообразной (релейной), петлевой, с зоной нечувствительности и т. п. Этот эффект сглаживания характеристики нелинейного звена позволяет, следовательно, ликвидировать влияние вредных гистерезисных петель, зоны нечувствительности, эффекта сухого трения и пр. по отношению к медленно меняющимся сигналам. В некоторых же случаях вибрационное сглаживание может оказаться отрицательным явлением, как было в случае рис. 19.8, где получался эффект снижения коэффициента усиления. Кроме этих явлений, аналогичных вибрационному сглаживанию при автоколебаниях, здесь появляются и принципиально новые явления вследствие зависимости характеристики Ф (х°) от В и сов, что будет подробнее рассмотрено ниже. Плавность функции смещения Ф (х°) (рис. 21.8, а) позволяет произвести обычную линеаризацию, а именно на некотором участке вблизи начала координат можно принять

(21.42)

где

(21.43)

Тогда все медленно протекающие процессы в данной нелинейной системе можно будет рассчитывать не по уравнению (21.41), а по линейному уравнению

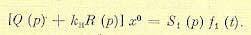(21.44)

При этом очень существенно то, что коэффициент усиления kн (рис. 21.8, а) будет зависеть не только от структуры и параметров самой системы, как было при автоколебаниях, но также и от амплитуды В и частоты wв внешнего периодического воздействия, которые могут меняться в известных пределах независимо от самой системы. Поэтому вибрационное сглаживание нелинейных характеристик при помощи вынужденных колебаний обладает значительно большими практическими возможностями, чем при автоколебаниях, и довольно часто применяется в технике, особенно в релейных системах автоматического управления. Однако в некоторых случаях

частоту вибраций wв, можно определить для заданного значения параметра k зависимость критической амплитуды внешних вибраций от частоты (рис. 21.9, в) — границу вибрационной помехоустойчивости системы.

Важно при этом иметь в виду, что при изменении параметров системы меняется и коэффициент kн и очертание функции смещения Ф (х°). Поэтому, строя области устойчивости системы по какому-нибудь параметру k (рис. 21.9), нужно соответственно все время менять величину kн в уравнении (21.44) или Ф (х°) в (21.41), т. е. при построении области устойчивости нужно учитывать, что любой параметр системы k может входить не только в состав R(р) и Q(р), но также и в состав величины kн. Зависимость же величины kн от любого параметра системы нетрудно найти предварительно согласно § 21.2 (см., например, рис. 21.8, в).

Кроме исследования устойчивости нелинейной системы можно по уравнению (21.41) или (21.44) провести полный анализ всех динамических качеств нелинейной системы, подверженной внешним вибрациям (качество переходных процессов, статические и динамические ошибки), при любых медленно меняющихся по сравнению с вибрациями внешних воздействиях f1(t).

По указанным уравнениям могут определяться и вынужденные колебания системы на низких частотах, если медленно меняющееся воздействие f1 (t) изменяется периодически, т. е. имеется возможность исследования двухчастотных вынужденных колебаний нелинейной системы при большой разнице частот. Можно и здесь (как в § 19.2) проводить разделение общего движения нелинейной системы не только на два, но и на три вида по степени медленности движения во времени.

В результате всех перечисленных расчетов будет выявлена специфическая для нелинейных систем зависимость всех статических и динамических качеств и даже ее устойчивости от величины амплитуды В и частоты wв внешнего периодического воздействия (вибраций), что в некоторых случаях на практике может оказаться решающим для создания качественной автоматической системы.

Изложенная общая теория поведения нелинейных автоматических систем при наличии внешнего периодического воздействия (вибраций) может значительно упрощаться в различных частных задачах.

Приведем здесь видоизменение этой общей теории для следующих двух наиболее типичных частных задач;

1)приложение специального внешнего периодического воздействия с целью вибрационного сглаживания нелинейности (с последующей линеаризацией сглаженной характеристики при расчете системы в целом);

2)исследование работы нелинейной автоматической системы при высокочастотных внешних вибрационных помехах, когда не все звенья системы пропускают эти вибрации.

Задача 1. Когда в любой автоматической системе прикладывается внешнее периодическое воздействие f2 (t) (рис. 21.10) специально для того, чтобы произвести вибрационное сглаживание нелинейности, то обязательно ставится условие, чтобы на выходе амплитуда вынужденных колебаний х3 была практически ничтожной. В результате этого переменные х3 и х1 (рис. 21.10) практически не будут содержать колебательной составляющей, а будут определяться через медленно меняющееся воздействие f1(t) по уравнениям типа (21.41) или (21.44). Поэтому переменная х на входе нелинейного звена будет

(21.46)

Следовательно, в данной задаче (вибрационная линеаризация нелинейности при помощи вынужденных колебаний) нет необходимости в решении уравнения 1(21.32) или (21.33) для определения колебательных составляющих, ибо, согласно (21.26), ,уже имеется готовое решение

(21.47)

Поскольку внешнее периодическое воздействие f2 (t) предполагается приложенным к системе непосредственно там же, где и х (рис. 21.10), то в уравнении (21.24), составленном для исследуемой части системы (не включая пунктирной части на рис. 21.10), будет

(21.48)

На основании (21.47) по первой из формул (21.28) находим

что и дает искомую сглаженную характеристику. При этом можно воспользоваться для всех типовых нелинейностей готовыми формулами из главы 19 и их графиками типа рис. 21.6, а, заменив везде а и ав на величину В. Как видим, здесь совершенно отпадает описанное в § 21.2 особое определение функции смещения Ф (х°).

В результате сглаженная характеристика F° (х°) будет иметь крутизну, зависящую в общем случае от амплитуды В и частоты wв внешних вибраций. Если же имеется нелинейность менее общего вида, а именно F(х), то частота сов не войдет в выражение для F°, как, например, в случае рис. 21.6, а. Однако все же и в этом случае нужно потребовать, чтобы частота содержалась в определенных пределах, позволяющих считать воздействие f1 (t) по сравнению с f2 (t) медленно меняющимся.

Определив таким образом сглаженную характеристику F° (х°), можно затем по уравнению типа (21.31) или (21.44) с использованием линеаризации (21.45) исследовать любые медленно протекающие процессы в системе в целом обычными методами теории регулирования. Заметим, что линеаризация по формуле (21.45) в данной задаче справедлива для любых форм нелинейностей, так как здесь частная производная по х° совпадает с полной производной.

Что касается уравнения для колебательных составляющих (21.32) или, что то же самое, (21.33), то его нужно использовать в данной задаче только для определения желательной величины частоты wв внешнего периодического воздействия f2 (t), обеспечивающей возможность получения решения (21.47) для вынужденных колебаний и выполнение сделанного выше предположения о малости вынужденных вибраций на выходе системы х3. С этой целью подставим равенства (21.47) и (21.48) в уравнение (21.33). Тогда для удовлетворения последнего уравнения необходимо потребовать, чтобы модуль отношения

был очень мал. Следовательно, частота внешнего периодического воздействия wв должна лежать за пределами полосы пропускания частотной характеристики всей линейной части рассматриваемого участка системы (блоки 1 и 2).

Кроме того, чтобы амплитуда вынужденных вибраций на выходе системы хв была ничтожна, нужно взять частоту сов также и за пределами полосы пропускания отдельного блока 2 исследуемой системы (рис. 21.10).

Задача 2. Пусть на какую-нибудь систему автоматического управления (рис. 21.11) воздействует внешняя вибрационная помеха

Р° или взять на графике рис. 21.6, а значение ав, определяемое по формуле (21.50) или графиком рис. 21.12. Поэтому, в отличие от задачи 1, здесь даже для простейших нелинейностей очертание характеристики нелинейного звена по полезному сигналу Р° (х°) и ее крутизна

будут зависеть не только от амплитуды В, но и от частоты wв вибрационных помех, а также, конечно, и от параметров линейных блоков 1 и 2 (рис. 21.11), входящих в формулу

(21.50).

Рассмотрим далее другой случай, когда первая гармоника вибраций с заданной частотой wв пропускается линейной частью системы с передаточной функцией (21.49), но все же не пропускается каким-либо одним блоком системы. Пусть, например, в схеме на рис. 21.11 вибрации не пропускаются вовсе только управляемым объектом, а по внутренней обратной связи первая гармоника вибраций с частотой wв проходит. Тогда, вообще говоря, уже нельзя не считаться с зависимостью (21.34) амплитуды вибраций переменной х от величины полезного сигнала х°. Однако и в этом случае возможно упрощение решения задачи по сравнению с общей теорией, состоящее в том, что при определении функции смещения выбрасывается часть системы, не пропускающая вибраций (рис. 21.13,

а).

В этом случае нужно записать уравнение динамики только оставшейся части системы

(рис. 21.13, а):

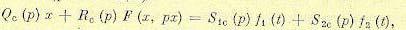(21.51)

которое будет, конечно, проще общего уравнения (21.24). Отсюда по аналогии с (21.35) получим уравнение для определения амплитуды вибраций на входе нелинейного звена в виде

где через Х2с, Y2с и Хс, Yс обозначены вещественные и мнимые части соответственно для S2с (jwв) и для выражения

Написанное уравнение позволяет определить зависимость амплитуды вибраций ав от

величины полезного сигнала х° на входе нелинейного звена для каждой заданной внешней вибрационной помехи графическим приемом, описанным в § 21.2 (рис. 21.7). Полученная зависимость а(х°) подставляется затем в первую из формул (21.29) для получения функции смещения F° = Ф (х°), которая в данном случае и будет являться характеристикой нелинейного звена по полезному сигналу. Вид ее будет зависеть от заданных амплитуды В и частоты wв внешних вибраций и от параметров системы, входящих в выделенную часть контура (рис. 21.13,а).

Вобоих рассмотренных случаях, проведя линеаризацию F° = Фх° характеристики нелинейного звена ;F° (х0) или Р° = Ф (х°) по полезному сигналу, можно обычными методами теории автоматического регулирования, используя линейные уравнения (21.44), выявить зависимость всех статических и динамических качеств данной нелинейной системы автоматического управления (и ее устойчивости) от амплитуды В и частоты сов вибрационных помех.

Линейная система выходила бы из строя при наличии помех тогда, когда полезный сигнал практически перестал бы различаться на фоне помех. Но пока он нормально различается, все статические и динамические свойства системы по полезному сигналу, если система линейна, остаются неизменными. Вибрационная помеха при этом накладывается как дополнительная ошибка. Совсем иначе дело обстоит в нелинейной

системе. Коэффициент усиления kн полезного сигнала в нелинейном звене, а вместе с ним и все качества и даже устойчивость системы могут настолько существенно зависеть от

помехи (от В и wв), что система может выйти из строя по этой причине раньше, чем перестанет различаться полезный сигнал на уровне помех. Это очень важно учитывать на практике.

С точки зрения упрощения решения задачи нужно всегда иметь в виду упрощенную формулу линеаризации (21.45), которая позволяет и во втором из рассмотренных случаев обходиться без определения функции смещения. В этом случае нужно подставить в

(21.45) значение амплитуды вибраций на входе нелинейного звена ав, найденное при отсутствии полезного сигнала (х° = 0) любым из двух методов, изложенных в § 21.1, но

для более простого уравнения системы (21.51). Зависимость ав(В) будет при этом, в отличие от первого случая, криволинейной (рис. 21.13, б).

Взаключение заметим, что тем же методом, что и в § 18.5, легко вычислять высшие гармоники вынужденных колебаний (см. § 9.4 книги [100]).